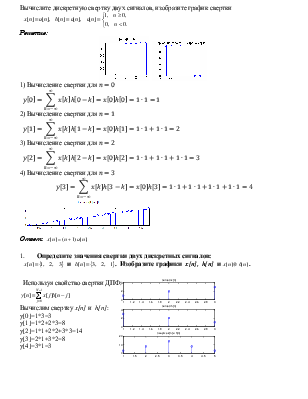


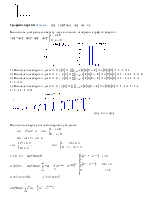






Вычислите дискретную свертку двух сигналов, изобразите
график свертки
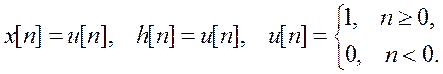
Решение:
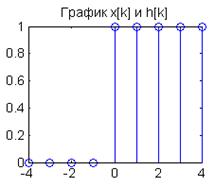
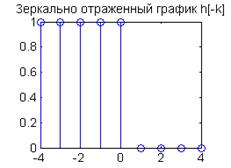
1) Вычисление свертки для ![]()
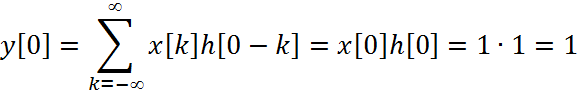
2) Вычисление свертки для ![]()
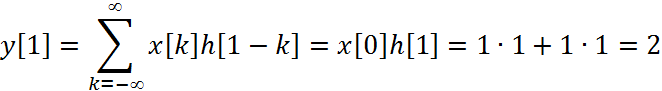
3)
Вычисление свертки для ![]()
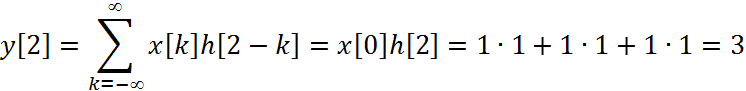
4)
Вычисление свертки для ![]()
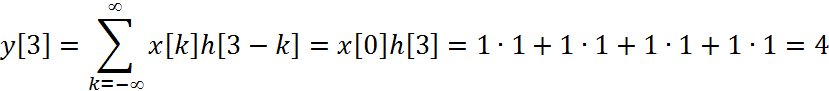
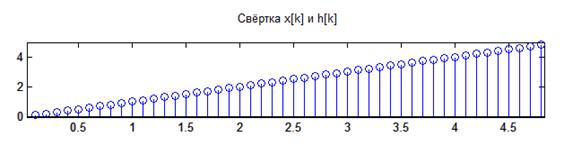
Ответ: ![]()
1.
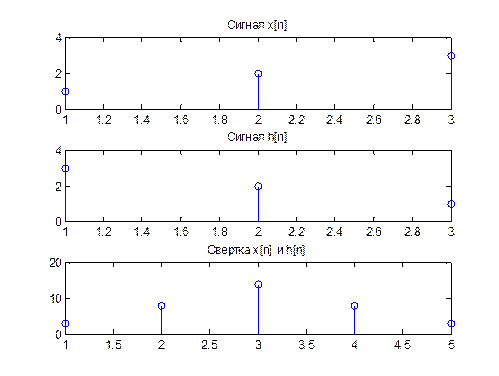 Определите значения свертки двух дискретных сигналов:
Определите значения свертки двух дискретных сигналов:
![]() и
и ![]() .
Изобразите графики x[n], h[n] и
.
Изобразите графики x[n], h[n] и ![]() .
.
Используя свойство свертки ДПФ:
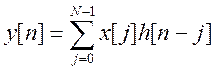
Вычислим свертку x[n] иh[n]:
y[0]=1*3=3
y[1]=1*2+2*3=8
y[2]=1*1+2*2+3*3=14
y[3]=2*1+3*2=8
y[4]=3*1=3
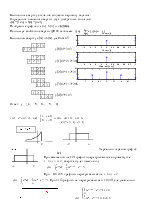
Рис.7. Графики сигналов и их свертки.
Ответ: y = { 3, 8, 14, 8, 3}.
Вычислите свертку двух непрерывных сигналов и
изобразите её график. 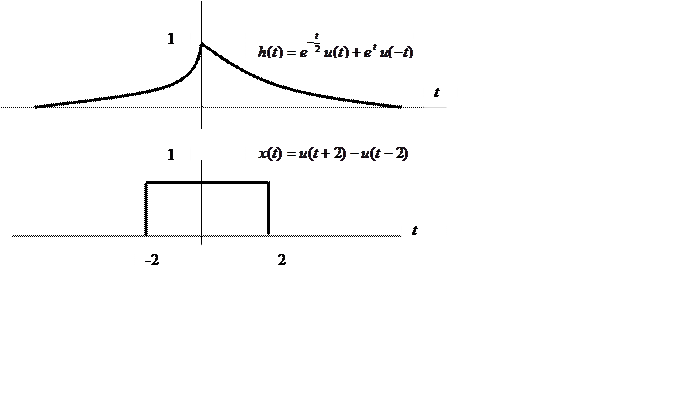
Интеграл непрерывной свертки имеет вид ![]() .
.
В соответствии с геометрическим смыслом операция свертки заключается в зеркальном отражении одной из участвующих в свертке функций, сдвиге её на значение t, перемножении операндов и интегрировании результата перемножения.
Зеркально отражать будем x(![]() )
)
Интервал интегрирования при этом разбивается на следующие подынтервалы:
1)
![]()
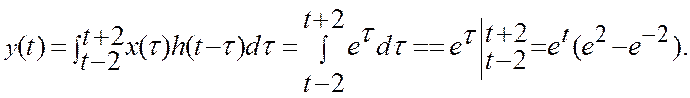
2)
![]()
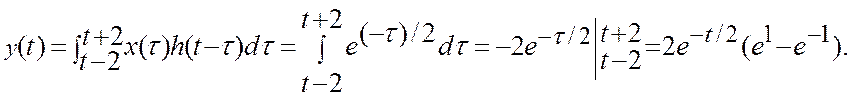
3)
![]()
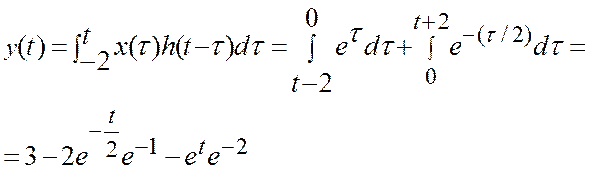
Таким образом, результат свертки
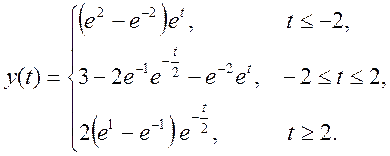
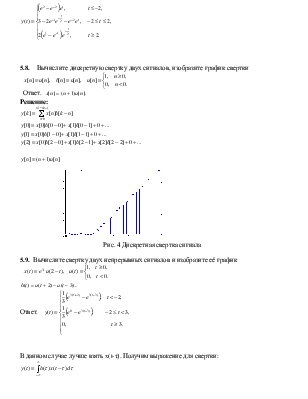
5.8.
Вычислите дискретную свертку
двух сигналов, изобразите график свертки
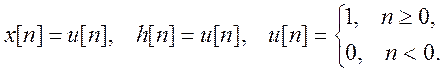
Ответ. ![]()
Решение:
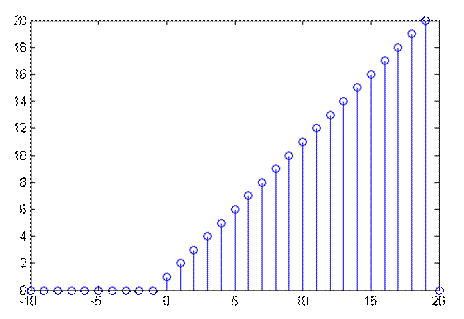 |
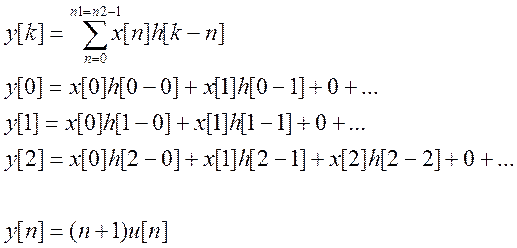
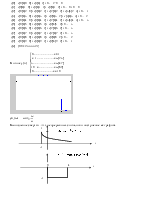
Рис. 4 Дискретная свертка сигнала
5.9. Вычислите
свертку двух непрерывных сигналов и изобразите её график
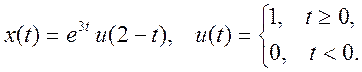
![]() .
.
Ответ. 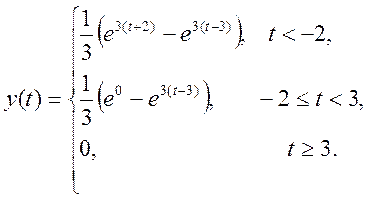
В данном случае лучше взять x(t-τ). Получим выражение для свертки:
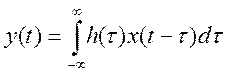
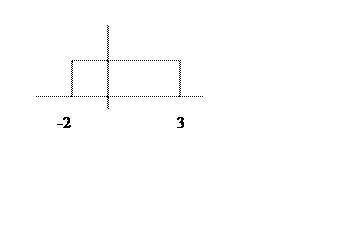
После «зеркального отображения» сигнала x(t), то есть x(-t), а так же его сдвиге на t=3, пересечение с сигналом h(t) будет равно нулю. Поэтому для всех t>3, y(t)=0. Для t, лежащего в интервале от -2 до 3, свертку необходимо искать в таком виде :
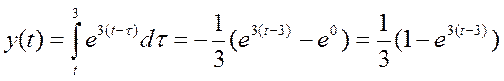
Если же t<= -2 то свертку надо искать так:
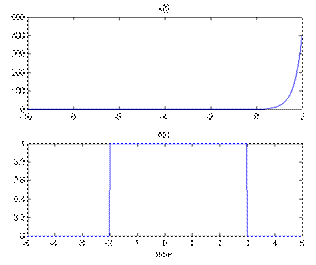
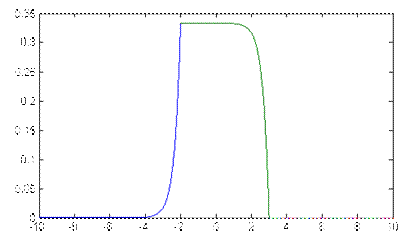
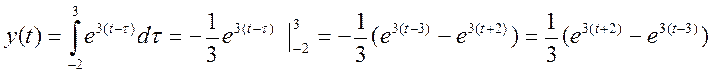
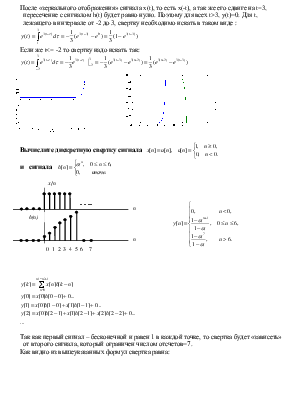
Вычислите дискретную свертку сигнала 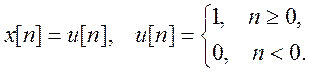
и сигнала 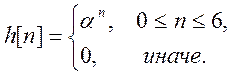
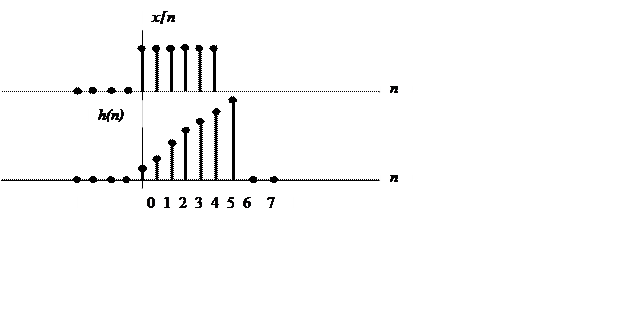
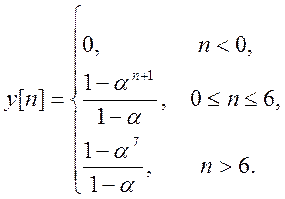 |
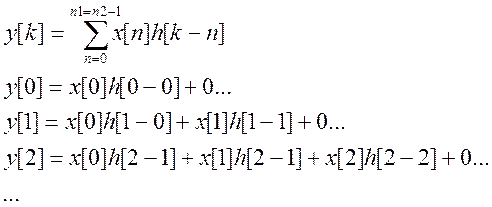
Так как первый сигнал – бесконечной и равен 1 в каждой точке, то свертка будет «зависеть» от второго сигнала, который ограничен числом отсчетов=7.
Как видно из вышеуказанных формул свертка равна:
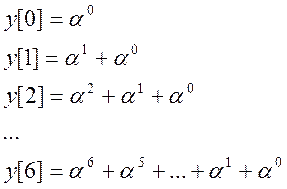
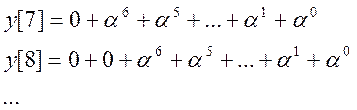
То есть свертка сигнала равна:
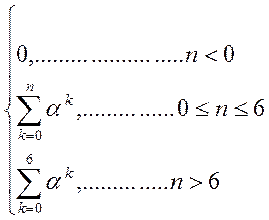
Если ![]() <0, то сумма
является суммой бесконечно убывающей геометрической прогрессии.
<0, то сумма
является суммой бесконечно убывающей геометрической прогрессии.
Эту сумму можно представить в виде (смотреть ответ)
Вычислите свертку сигналов согласно варианту задания.
Определите значения свертки двух дискретных сигналов:
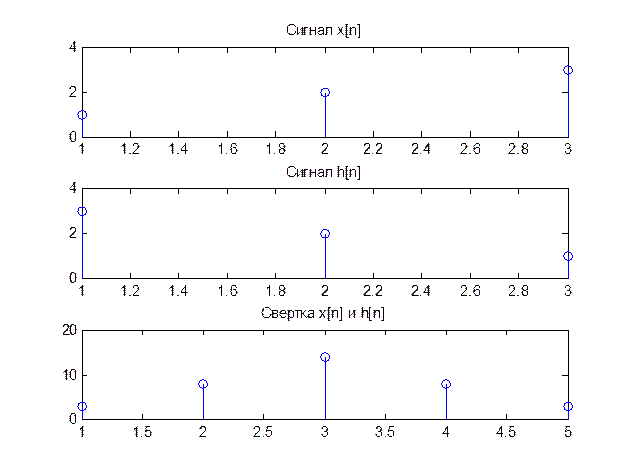
![]() и
и ![]()
Изобразите графики x[n], h[n] и ![]() .
.
Используя свойство свертки ДПФ, запишем: 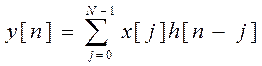
Вычислим
свертку x[n] и h[n] для 0![]() n
n ![]() 5:
5:
|
y[0]=1*3=3 y[1]=1*2+2*3=8 y[2]=1*1+2*2+3*3=14 y[3]=2*1+3*2=8 y[4]=3*1=3 |
|||||||||||||||||||||||||||||||||||||||||||||
Ответ: y = { 3, 8, 14, 8, 3}.
|
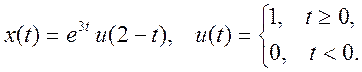 и
и
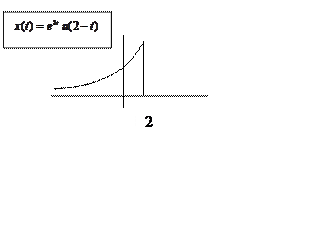
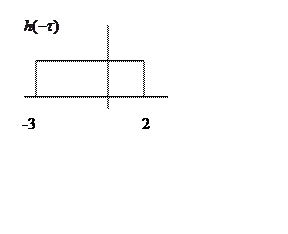
 Зеркально отразим график h(t):
Зеркально отразим график h(t):
При смещении на t<0 графики перекрываются в промежутке ![]()
![]() ,
свертка будет иметь вид:
,
свертка будет иметь вид:
![]()
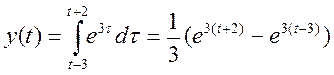 .
.
При ![]()
![]() графики перекрываются на
графики перекрываются на ![]()
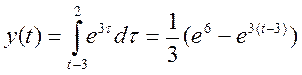 .
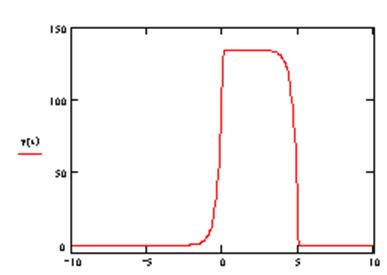
При t>5
графики не перекрываются и y(t)=0,
следовательно
.
При t>5
графики не перекрываются и y(t)=0,
следовательно
 |
|||
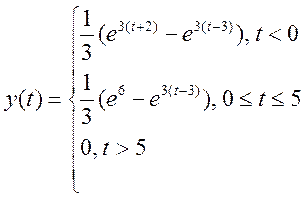 |
|||
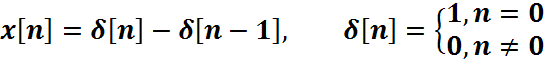
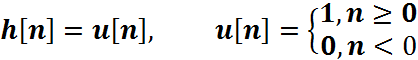
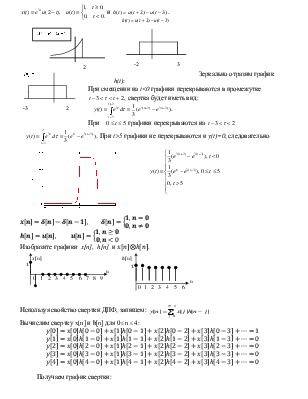
Изобразите
графики x[n], h[n] и ![]() .
.
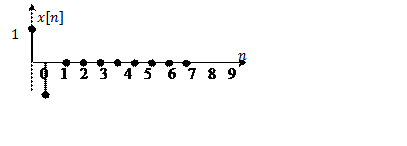 |
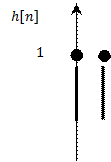 |
||||||||||||||
|
|||||||||||||||
|
Используя
свойство свертки ДПФ, запишем: 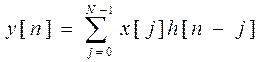
Вычислим
свертку x[n] и h[n] для 0![]() n
n ![]() 4:
4:
![]()
![]()
![]()
![]()
![]()
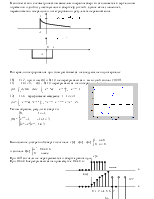
Получаем график свертки:
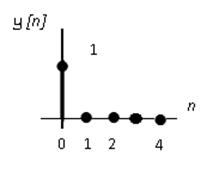
График свёртки Ответ. ![]()
Вычислите дискретную свертку
двух сигналов, изобразите график свертки
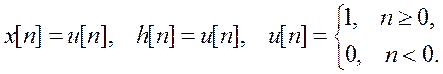
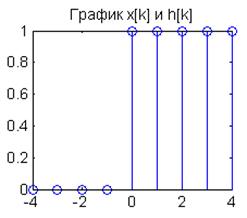
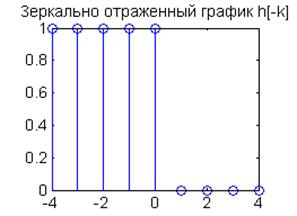
1) Вычисление свертки для ![]()
![]()
2) Вычисление свертки для ![]() ;
; ![]()
3) Вычисление свертки для ![]() ;
; ![]()
4) Вычисление свертки для ![]() ;
; ![]()
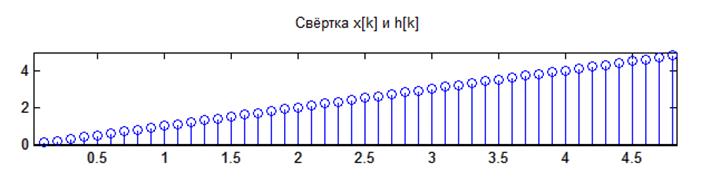
![]()
Вычислить свертку согласно варианту задания.
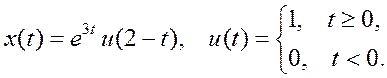
![]() .
.
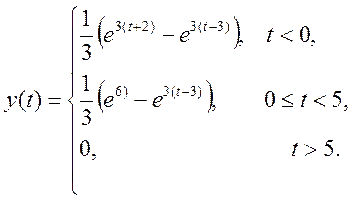
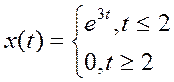 ,
, 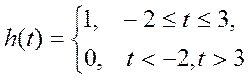
t-3>2 => x(t)*h(t)=0
t+2<2=> x(t)*h(t)=
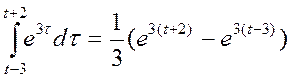
t+2>2 => t>=0, t-3<2 =>t<5
x(t)*h(t)= 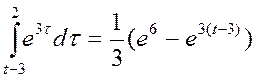
Вычислите свертку двух непрерывных сигналов и изобразите её график.
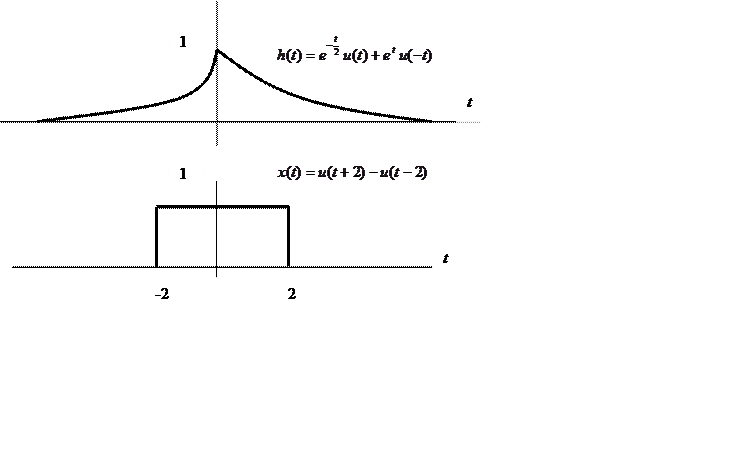 |
Интеграл
непрерывной свертки имеет вид ![]() .
.
В соответствии с геометрическим смыслом операция свертки заключается в зеркальном отражении одной из участвующих в свертке функций, сдвиге её на значение t, перемножении операндов и интегрировании результата перемножения.
Зеркально отражать
будем x(![]() )
)
Интервал интегрирования при этом разбивается на следующие подынтервалы:
4)
![]()
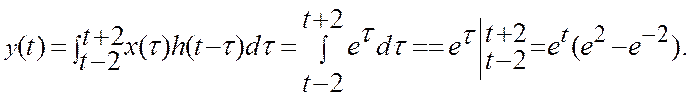
5)
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.