Система автоподстройки частоты

Федеральное агентство по образованию

Государственное общеобразовательное учреждение высшего профессионального образования

СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ

Кафедра «Радиотехнические системы»

КУРСОВАЯ РАБОТА

СИСТЕМА АВТОПОДСТРОЙКИ ЧАСТОТЫ

Пояснительная записка

                                                                                                                Выполнил:

                                                                                                                   ст-т гр. Р 54-2

                                                                                                                   А. Е. Шамова

                                                                                                               Проверил:

В. Н. Бондаренко

Красноярск 2007

 

Содержание

1.  Исходные данные………………………………………………………………….3

2.  Расчет параметров следящей системы…………………………………………...4

2.1  Определение передаточной функции………………………………………...4

2.2  Определение спектральной плотности эквивалентного шума, приведенного ко входу дискриминатора…………………………………….4

3.  Оптимизация следящей системы…………………………………………………5

3.1  Оптимизация следящей системы по параметру К_и………………………….5

3.2  Определение оптимального значения шумовой полосы……………………6

3.3  Построение графика зависимости ошибок слежения от полосы пропускания системы……………………………..…………………………...7

4.  Построение ЛАХ и ЛФХ разомкнутой системы………………………………...9

4.1  Логарифмическая амплитудно-частотная характеристика…………………9

4.2  Логарифмическая фазо-частотная характеристика………………………….9

4.3  Определение запаса устойчивости по амплитуде и фазе при оптимальном значении параметра К_и……………………………………………………….10

5.  Цифровое моделирование следящей системы………………………………….11

5.1  При ступенчатом воздействии………………………………………………13

5.2  При квадратичном воздействии……………………………………………..14

6.  Составление функциональной схемы следящей системы……………………..15

6.1 Список используемых сокращений…………………………………………21

7.  Перечень использованной литературы………………………………………….22

1.  Исходные данные

Номер варианта	№14
Тип следящей системы	АПЧ
Параметры задающего воздействия
Коэффициент передачи дискриминатора
Спектральная плотность шума
Параметры динамического звена: Число интегрирующих звеньев	k = 2
Число форсирующих звеньев	m = 1
Число инерционных звеньев
Постоянные времени инерционных звеньев	Т1 = 0,8, с                                                                                Т2 = 0, с
Область применения системы	Следящий измеритель дальности доплеровской спутниковой РНС

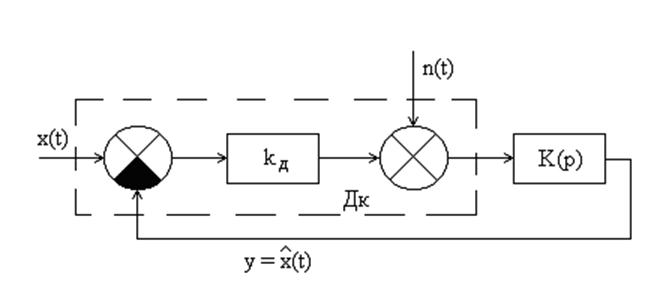
Рис.1.1 - Структурная схема следящей системы

 

2. Расчет параметров следящей системы

2.1 Определение передаточной функции

         Найдем передаточные функции разомкнутой системы Кр(р), а также замкнутой системы Кз(р), используя параметры системы описанные в задании на курсовой проект:

k=2 - число интегрирующих звеньев

m=1- число форсирующих звеньев

n-k=0 - число инерционных звеньев

Таким образом, передаточная функция разомкнутой системы К_p(р) определяется по формуле 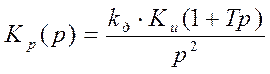(2.1):

(2.1)

Передаточная функция замкнутой системы Кз(р) определяется по формуле (2.2):

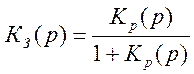
   (2.2)

Предварительно обозначив , подставляем (2.1) в (2.2):

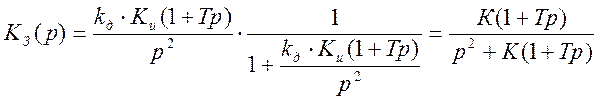                                                                                                                                                                                                                         (2.3)

2.2 Определение спектральной плотности эквивалентного шума, приведённого  ко входу дискриминатора

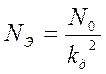          Используя правило преобразования структурных схем (перенос сумматора с выхода на вход звена), для спектральной плотности эквивалентного шума n_э(t), приведённого  ко входу дискриминатора (вход элемента сравнения) можно записать (2.4):

(2.4)

         

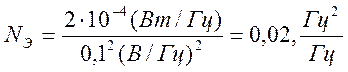
3. Оптимизация следящей системы

3.1 Оптимизация следящей системы по параметру К_и

     Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению значения параметра K_и, при котором обеспечивается минимум величины:

                    (3.1)

где - составляющая, которая определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию;

   - определяет дисперсию ошибки , обусловленную помехой n(t).

           Следовательно, (3.1) определяет средний квадрат результирующей ошибки

      .

Динамическая ошибка  определяется параметрами  и  задающего воздействия, а также порядком астатизма (числом интеграторов) и добротностью   системы. Для системы 2-го порядка установившаяся ошибка  равна:

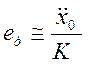                                                                                                               (3.2)

     где K, c^-2 - добротность системы по ускорению (k=2).

Случайная составляющая е_n(t) ошибки определяется статистическими характеристиками помехи n(t) и структурой (а также параметрами) системы. В качестве n(t) используем модель белого шума, с равномерной в полосе частот от 0 до ∞, спектральной плотностью (хотя реальный шум имеет ограниченную ширину спектра, однако она во много раз превышает полосу пропускания системы F_ш, что позволяет использовать модель белого шума). Исходя из этого, дисперсию шумовой ошибки рассчитаем по формуле:

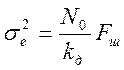            , Гц                                                                                                          (3.3)

где 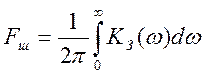                                                                                                (3.4)

     - шумовая полоса следящей системы в Гц; - АЧХ замкнутой системы.

Для нахождения экстремума среднего квадрата ошибки необходимо продифференцировать выражение (3.1) по параметру К_и и приравнять производную нулю:

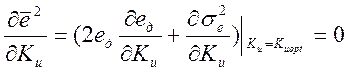                                                                                     (3.5)

Для вычисления интеграла (3.4) представим подинтегральное выражение в виде: