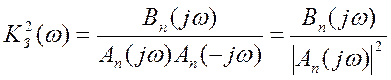Система автоподстройки частоты, страница 2

                                                                              (3.6)

 где  

          - полиномы;                                            (3.7)                                                                                                                                                                                                                                

         n- порядок дифференциального уравнения, описывающего систему.

3.2 Определение оптимального значения шумовой полосы

Нахождение шумовой полосы системы и дисперсии шумовой ошибки сводится к вычислению интеграла:

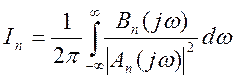          ,                                                                                          (3.8)

   значение которого при n=2:

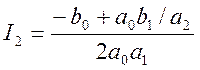                                                                                                            (3.9)

            Заменим в выражении (2.3) параметр p на jω. Получим:

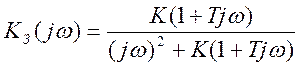                                                                                         (3.10)

         Представим выражение (3.10) в виде (3.6):

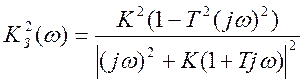                                                                                        (3.11)

         Отсюда получаем:

        

         

         В соответствии с  выражением (3.7) получаем:    

         a₀=1; a₁=KT; a₂=K

         b₀=-K²T²;  b₁=K².

         Подставим полученные коэффициенты в (3.9):

         

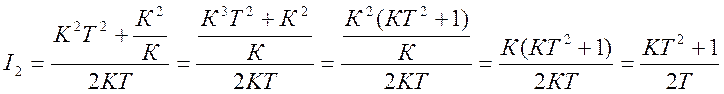
         Найдем шумовую полосу:                                                    

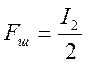                                                                                                                        (3.12)

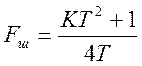                   (3.13)

         Дисперсия шумовой ошибки:

                                                                                

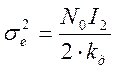
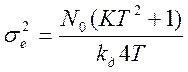                                                                                                         (3.14)

         Подставим выражения (3.2) и (3.14) в (3.5):

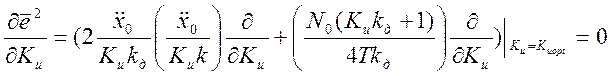                                               (3.15)

         Выполнив математические преобразования, получим:

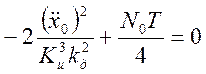                                                                                                         (3.16)

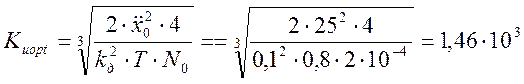           , с^-2        

Зная величину K_иopt по формуле (3.13) рассчитываем оптимальное значение шумовой полосы F_шoptсистемы:

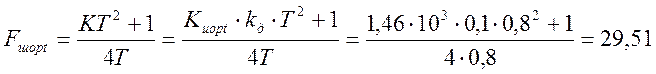            , Гц

      По формуле (3.1) определяем минимально достижимую ошибку слежения: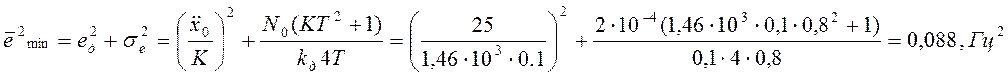 

3.3 Построение графика зависимости ошибок слежения от полосы пропускания системы

       Для построения графика зависимости , необходимо установить связь между  и  через коэффициент К:

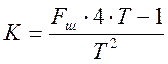                                                                                                            (3.17)

           Опираясь на выражение (3.2), получаем:

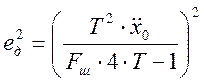           (3.18)

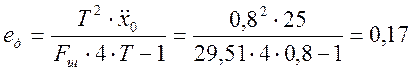             , Гц                                                         (3.19)

 

          Дисперсия шумовой ошибки определяется по формуле (3.3):

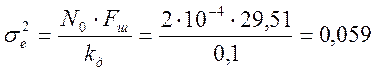          , Гц²                                                                     

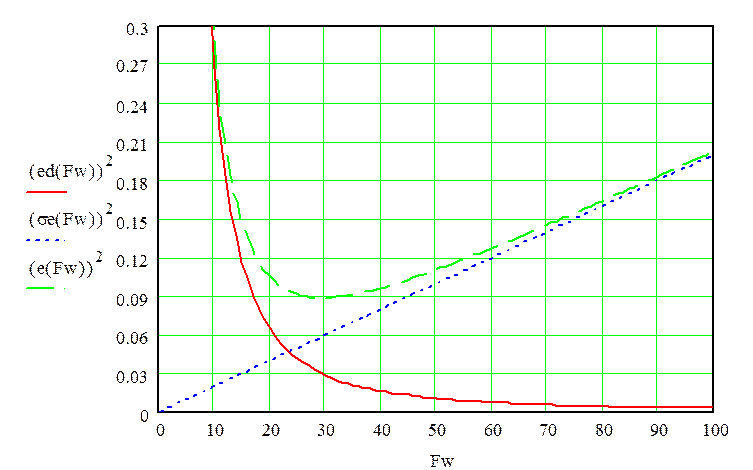
Рис. 3.1 - График зависимости ошибок слежения от полосы пропускания системы:

      -  - квадрат динамической ошибки

                            _ _ _ _ _ -  - дисперсия шумовой ошибки

                            __ __ __ - - результирующая ошибка

4.  Построение ЛАХ и ЛФХ разомкнутой системы

4.1   Логарифмическая амплитудно-частотная характеристика

Для определения запаса устойчивости системы построим логарифмическую амплитудно-частотную и фазо-частотную характеристики, по которым установим запас по усилению и фазе.

Передаточная функция разомкнутой системы имеет вид:

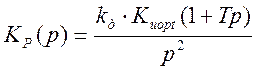            ,                                                                                         (4.1)

где К_иopt

k_д =0,1  В/Гц

T =0,8 c

Из исходных данных известно, что передаточная функция разомкнутой системы задается 1 форсирующим звеном (m=1) и двумя интегрирующими (k=2).

Тогда ЛАХ разомкнутой системы имеет вид:

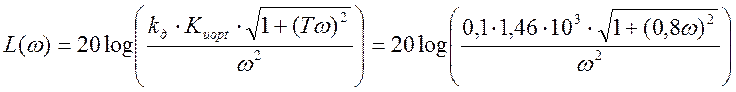                            (4.2)

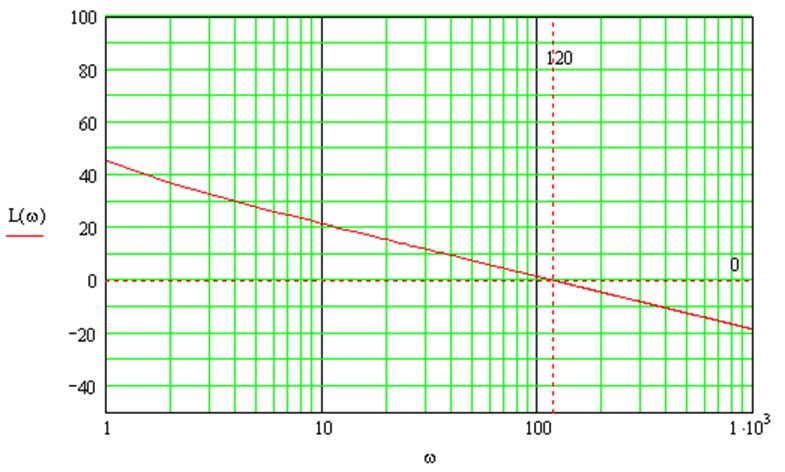
Рис. 4.1 – ЛАХ разомкнутой системы

4.2 Логарифмическая фазо-частотная характеристика

ЛФХ разомкнутой системы имеет вид:

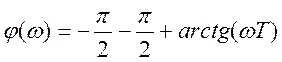                                                                                         (4.3)

 

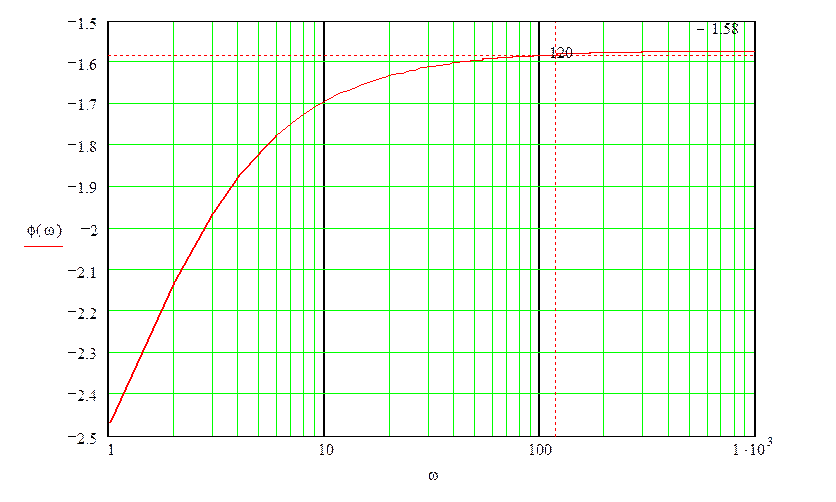
Рис. 4.2 – ЛФХ разомкнутой системы

4.3 Определение запаса устойчивости по амплитуде и фазе при оптимальном значении параметра К_и

Запас по амплитуде (усилению) численно равен значению ЛАХ на критической частоте, т. е. частоте, на которой ЛФХ равна -π рад. Из Рис. 4.2 видно, что ЛФХ не пресекает горизонтальную прямую , значит запас по амплитуде (усилению) ΔL не имеет смысла определять.

Тогда запас устойчивости определяется одним показателем – запасом по фазе.

Запас по фазе определяется как:

                                                                       (4.4)

Из Рис. 4.1 и Рис. 4.2 видно, что запас по фазе составляет Δφ≈1,56 рад.

Считаем, что система является устойчивой, так как полученный запас по фазе Δφ удовлетворяет условию Δφπ/6.  

5. Цифровое моделирование следящей системы

Для моделирования линейной непрерывной системы по её передаточной функции воспользуемся методом билинейного преобразования. Суть его состоит в том, что непрерывные интегрирующие звенья, входящих в систему, заменяют дискретными интеграторами, осуществляющими интегрирование по методу трапеций.

Дискретная передаточная функция цифровой модели следящей системы при использовании метода билинейного преобразования получается из передаточной функции замкнутой непрерывной системы путем замены оператора непрерывного интегрирования:

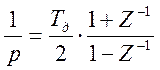,                                                                                                   (5.1)

где Т_д – интервал дискретизации, выбираемый в соответствии с теоремой Котельникова из условия:

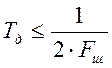                                                                                                                                (5.2)

                                   

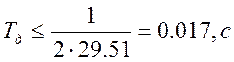
Полученную в результате дискретной аппроксимации (5.1) передаточную функцию цифровой модели системы необходимо представить в виде:

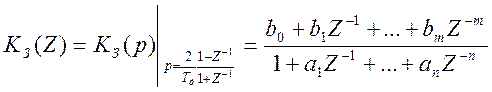                                                                          (5.3)

Передаточной функции (5.3) соответствует разностное уравнение:

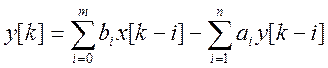                    ,                                                                             (5.4)

являющееся цифровой моделью следящей системы.

Для определения характеристик следящей системы в переходном режиме воспользуемся другой формой разностного уравнения: