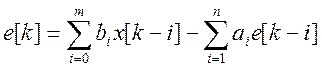Система автоподстройки частоты, страница 3

                    ,                                                                              (5.5)

записанной относительно ошибки слежения.

Коэффициенты разностного уравнения (5.5) определяются по передаточной функции:

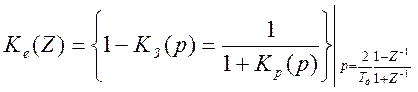                   ,                                                                 (5.6)

гдеК_е(Z) – дискретная передаточная функция для ошибки;

      К_р(р) – передаточная функция разомкнутой непрерывной системы.

 

Подставим (2.1) в (5.6):

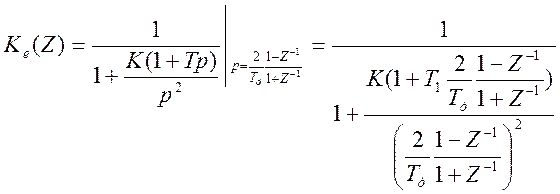,                                           (5.7)

гдеК_e(Z)-дискретная передаточная функция;

                       К- добротность системы, c^-2;

                   Т- постоянная времени (T=0,8 c);

                   Т_д- интервал дискретизации, c.

Выполним преобразования и перепишем формулу (5.7) в виде дробно-рациональной функции:

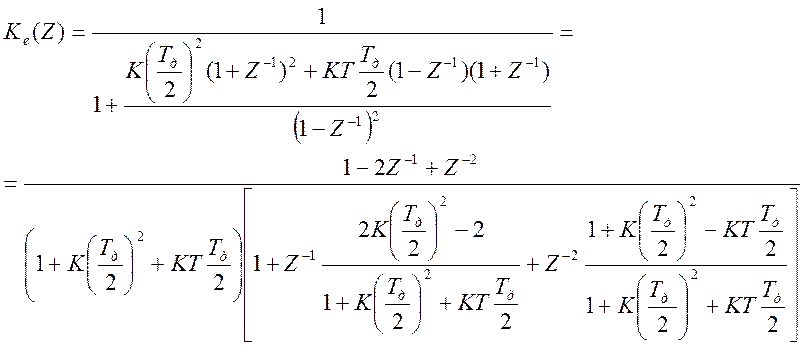                              (5.8)

Из формулы (5.8) определим коэффициенты {a_i} и {b_i}:

             

             

             

 

             

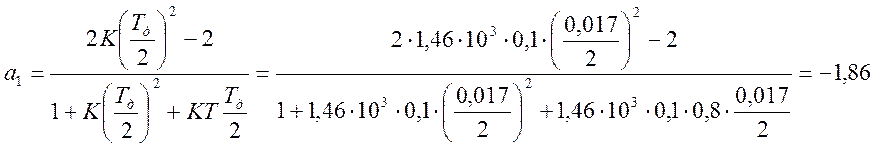
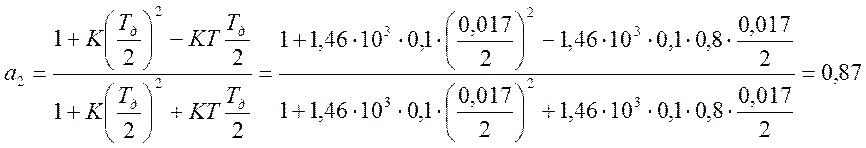
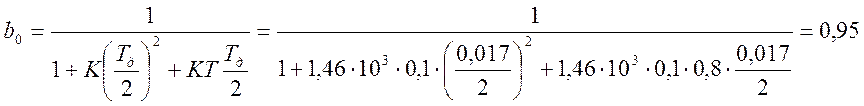
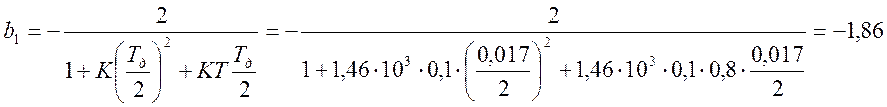
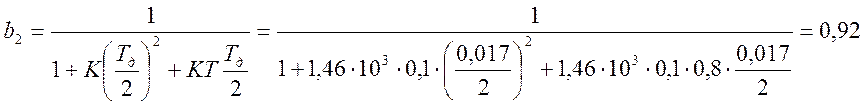
Передаточной функции (5.8) соответствует разностное уравнение:

                                                              (5.9)

           

5.1 При ступенчатом воздействии

Произведем моделирование при ступенчатом воздействии, которое определяется формулой:

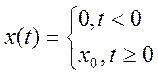                                                                                                    (5.10)

Поскольку характеристики переходного процесса не зависят от значения х₀ (нормированная зависимость  одна и та же при любом х₀), то при моделировании удобно принять х₀=const(t)=1. Значит:

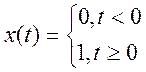
Переходный процесс относительно ошибки:

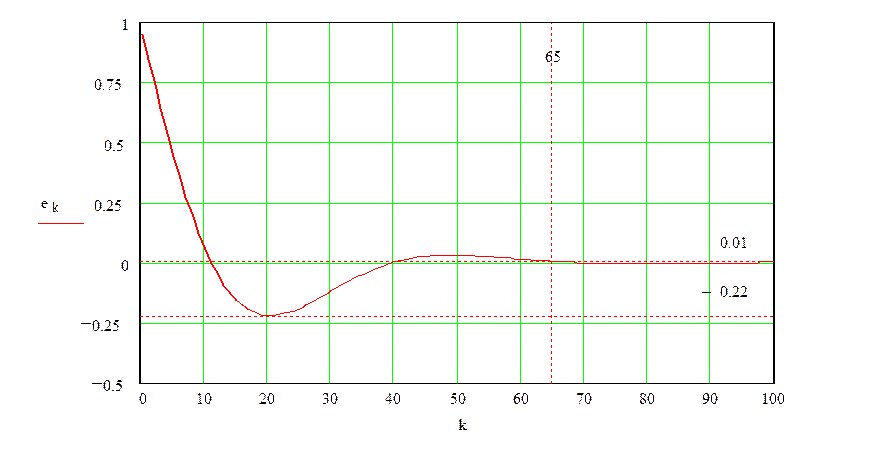
Рис. 5.1 - График зависимости е[k] для ступенчатого воздействия

Быстродействие системы определяется временем переходного процесса, в течение которого ошибка уменьшается по абсолютной величине до значения 0,01:

t_П=k_ПТ(5.11)

где k- дискретное время

       Т=Т_д=0,017, с – интервал дискретизации (5.2).

Из графика (Рис. 5.1) видно, что k=65, следовательно:

                       t_П=

 

Перерегулирование определяется величиной максимального выброса |e_max| в переходной характеристике. Величина максимального выброса:

 |e_max|=|-0,22|=0,22

       Перерегулирование:

ε=|e_max|=0,22 =22 %

Поскольку, обычно, для автоматических систем принимают допустимым ε≤30 %, то полученное значение (ε=22 %), находится в пределах допуска.

5.2 При квадратичном воздействии

Формирование дискретных значений квадратичного воздействия производится по формуле:

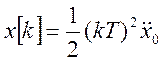
                                                                                               (5.12)

Переходный процесс относительно ошибки:

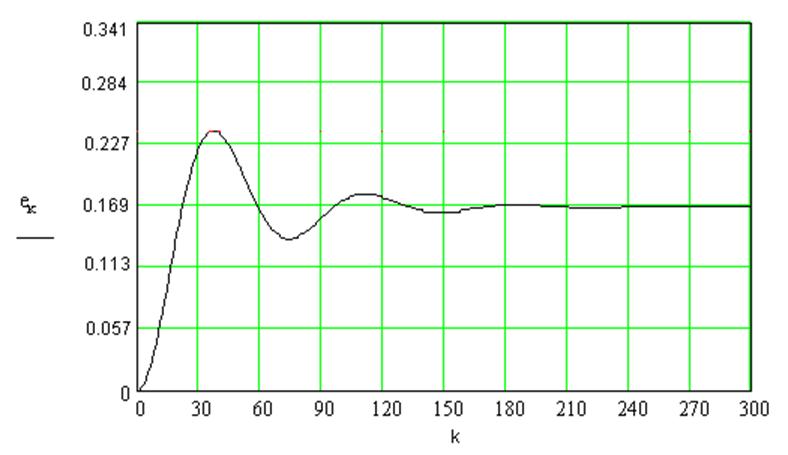
Рис. 5.2 - График зависимости е[k] для квадратичного воздействия

Из графика (Рис. 5.2) можно определить, что установившееся значение ошибки системы соответствует 0,17, Гц,что соответствует величине, рассчитанной по формуле (3.19).

6. Составление функциональной схемы следящей системы

Система АПЧ относится к классу следящих систем (систем слежения за частотой). Рассмотрим принцип действия данной системы.

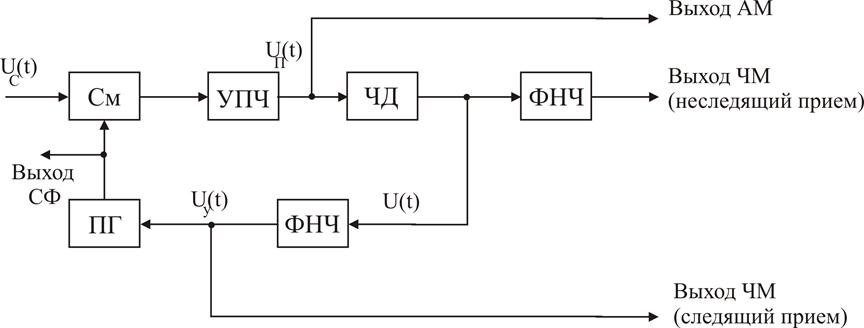
Рис. 6.1 – Функциональная схема системы АПЧ

Сигнал промежуточной частоты U_п(t) поступает на вход частотного дискриминатора (ЧД), назначением которого является формирование сигнала ошибки и как функции частотной расстройки Δf. Зависимость U(Δf) носит название дискриминационной характеристики (Рис. 6.2, а).

Если начальная расстройка Δf₀ не превышает по абсолютной величине некоторого значения Δf_з называемого полосой захвата, то под действием управляющего напряжения U_y(t), снимаемого с выхода ФНЧ, частота подстраиваемого генератора изменяется таким образом, что частотная расстройка Δf→0. Полоса захвата является важной характеристикой системы АПЧ. Она определяется шириной дискриминационной характеристики, усилением предшествующего дискриминатору тракта, характеристиками подстраиваемого генератора и другими факторами.

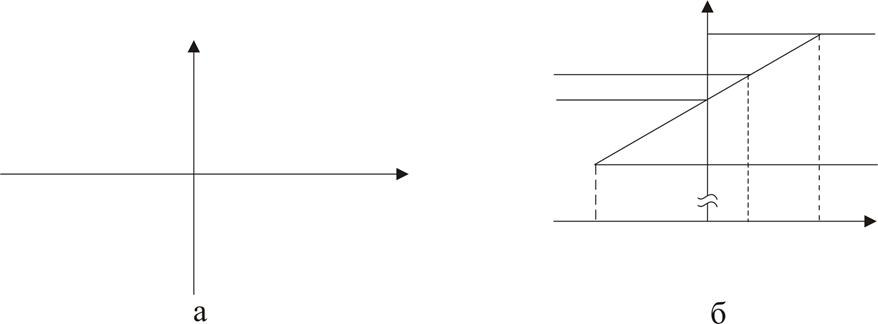
Рисунок 6.2. – Дискриминационная (а) и регулировочная (б) характеристики.

В качестве элемента, управляющего частотой ПГ, обычно используется варикап - полупроводниковый прибор, емкость которого зависит от управляющего напряжения. Зависимость частоты ПГ от управляющего напряжения носит название регулировочной характеристики (Рис. 6.2, б).

При начальной расстройке Δf₀ >0 на выходе дискриминатора формируется сигнал ошибки U_ош>0 (постоянное напряжение). Под действием этого напряжения частота fг возрастает (значение f_г0 соответствующее разомкнутой обратной связи, называется собственной частотой подстраиваемого генератора). При этом частотная расстройка уменьшается, поскольку Δf=f_c-f_г-f₀. При начальной расстройке другого знака частота ПГ, наоборот, уменьшается, что также приводит к устранению частотной расстройки.

Фильтр нижних частот отфильтровывает мешающие сигналы и высокочастотные составляющие шума, пропуская без искажений низкочастотную составляющую напряжения U(t) частотного дискриминатора, обусловленную медленным изменением частоты f_п (вследствие нестабильностей частот передатчика и гетеродина, а также эффекта Доплера).

Таким образом, система АПЧ обеспечивает постоянство промежуточной частоты (с точностью до ошибки, обусловленной шумом и инерционностью системы), компенсируя уход частоты из-за нестабильности и эффекта Доплера. Это позволяет использовать УПЧ с узкой полосой пропускания (равной ширине спектра сигнала), а следовательно, существенно ослабить мешающее влияние шумов и таким образом повысить помехозащищенность приемника.

Доплеровские СРНС относятся к системам 1-го поколения. Примером доплеровской СРНС является разработанная в США и введенная в 1964 г. В эксплуатацию система “Транзит”.

Метод определения местоположения потребителей доплеровской СРНС представлен на (Рис. 6.3).

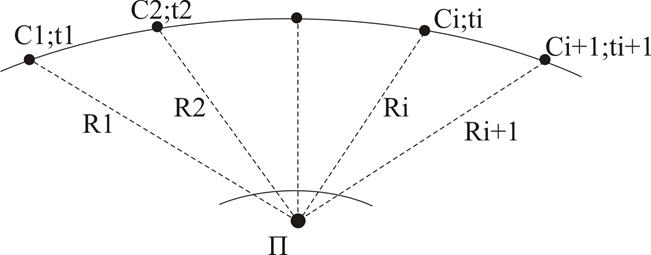
Рис. 6.3 – Определение координат потребителя доплеровской  СРНС:

Ci;ti – последовательные положения НИСЗ на орбите,

 разделенные интервалом времени Т;

П- потребитель (определяющийся объект);

Ri (i=1,2…) - расстояние между П – и i-м положением НИСЗ.

 

Измеряя разность расстояний ΔR1=R2-R1, получают одну линию положения – гиперболу, соответствующую постоянному навигационному параметру ΔR1 (гипербола получается как линия пересечения гиперболоида вращения с фокусом в точках С1 и С2 и геоида – поверхности Земли). Второе измерение ΔR2=R3-R2 дает вторую линию положения. Пересечение двух линий положения определяет координаты потребителя. Для определения местоположения потребителя в пространстве (самолета, космического аппарата) требуется дополнительное измерение ΔR3=R4-R3. Местоположение потребителя находится как точка пересечения трех поверхностей положения – гиперболоидов.