Синтез фильтров с несимметричными частотными характеристиками методом отражения координат

1.7.  Синтез фильтров  с несимметричными частотными

характеристиками методом отражения координат

        Во многих случаях  требования к уровню заграждения полосовых фильтров в верхней и нижней полосах заграждения неодинаковы.  Наиболее характерен случай радиостанций с дуплексной связью, где фильтр приёмника должен обеспечивать большое ослабление сигнала своего передатчика. Обычные фильтры с симметричными характеристиками (полиномиальные, эллиптические) в этом случае оказываются избыточными.

      Сочетание в одной схеме функций пропускания и заграждения позволяет уменьшить количество реактивных элементов. Синтез подобных фильтров может быть основан на частотном преобразовании низкочастотного прототипа с помощью функционала преобразования, подбор которого осуществляется исключительно эвристическим методом [104–106].

     В [107, 108] описаны методы синтеза волноводных фильтров с несимметричными характеристиками, которые названы односторонними фильтрами (single-sided filters). Метод предназначен для проектирования только волноводных структур.

     Ниже изложен другой метод синтеза подобных фильтров.  Такие фильтры имеют самостоятельное значение в низкочастотной технике и могут служить прототипом для построения СВЧ селективных схем на распределённых элементах.

1.7.1.  Трёхэлементные контуры

      Фильтры с несимметричными характеристиками могут быть построены на трёхэлементных контурах – цепях с двумя резонансами, которые являются элементарным звеном фильтров с несимметричными характеристиками.

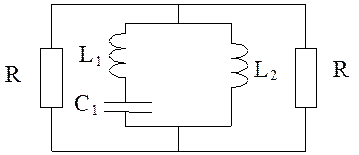
     Рассмотрим контур с двумя индуктивностями в параллельном включении (рис. 1.7.1).

Резонансными частотами такого контура  являются:

частота пропускания    

                                           ;                                                 (1.7.1)

частота режекции                      

                                                     .                                                 (1.7.2)

             Рис. 1.7.1. Трёхэлементный контур

Проводимость контура

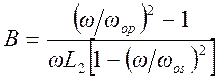.                                                 (1.7.3)

Нагруженная добротность в полосе пропускания (индекс p–pass)

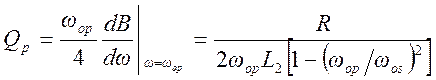.               (1.7.4)

При заданных частотах  и добротности Q_p из (1.7.1), (1.7.2), (1.7.4) находятся параметры элементов L₂, C₁, L₁.

     Функция фильтрации контура (элемент волновой матрицы передачи) [7, 22]

.

     С учётом (1.7.3) и (1.7.4) имеем

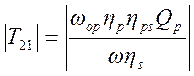                                                     ,                                     (1.7.5)

где частотные переменные:

в полосе пропускания

                                                     ;                                          (1.7.6)

в полосе заграждения (режекции)

                                                    ;                                            (1.7.7)

перекрёстная частотная переменная   

                                                    .                                      (1.7.8)

Тогда функция рабочего затухания L и рабочее затухание aзапишутся как

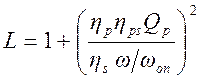                                                        ;                                       (1.7.9)

                                                            .                                           (1.7.10)

Таблица 1.7.1. Эквивалентность трёхэлементных контуров

. ;. ;

Таблица 1.7.2. Параметры трёхэлементных контуров

Схема, АЧХ		Формулы для анализа	Формулы для синтеза
1a. Квази-ФНЧ	;
1б. Квази-ФНЧ
2a. Квази-ФНЧ

Табл.1.7.2. Продолжение

Схема, АЧХ	Формулы для анализа	Формулы для синтеза
2б. Квази-ФНЧ	;
3a. Квази-ФВЧ	;
3б. Квази-ФВЧ

Табл.1.7.2. Окончание

Схема, АЧХ	Формулы для анализа	Формулы для синтеза
4a. Квази-ФВЧ
4б. Квази-ФВЧ

Аналогичные расчёты проводятся и для других  трёхэлементных  контуров. Трёхэлементные контуры могут быть представлены в двух  эквивалентных формах.  Формулы эквивалентности даны в таблице 1.7.1 [28].

          В  табл. 1.7.2 приведены параметры  трёхэлементных контуров.  Пропускающие контуры  с крутым высокочастотным скатом (схемы 1а, 1b, 2а, 2b в табл., при )  названы квази-ФНЧ (фильтры нижних частот), а с крутым низкочастотным скатом – квази-ФВЧ (фильтры верхних частот) (схемы 3а, 3b, 4а, 4b, при   ).

1.7.2. Фильтры на трёхэлементных контурах

    Многозвенные фильтры строятся по лестничной схеме. Как и в случае одиночных контуров будем использовать названия квази - ФНЧ и квази - ФВЧ.

    При переходе от контуров к фильтрам вместо частотных переменных  (1.7.6), (1.7.7) введём нормированные частотные переменные:

      для полосы пропускания

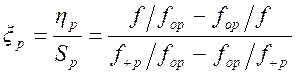                                               ;                              (1.7.11)

     для полосы режекции

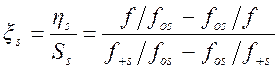                                               ,                               (1.7.12)

где – текущие частотные переменные, ,  – масштабные частотные множители по терминологии [7]; индекс p относится к полосе пропускания, s – к полосе заграждения (режекции):

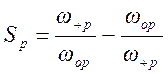                                                        ;                                       (1.7.13)

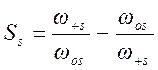                                                         .                                        (1.7.14)

Среднегеометрические частоты

                                                                                                 (1.7.15)

                                                        ,                                          (1.7.16)

где ,  и ,  – нижняя и верхняя частоты полос пропускания и режекции соответственно.

При  можно использовать среднеарифметические значения.

    У одиночного контура при введении третьего элемента увеличивается      добротность и  смещается резонансная частота в сторону более крутого ската при фиксированной верхней частоте полосы пропускания (для квази - ФНЧ контура) при той же ширине полосы на уровне 3,01 дБ.

    При чебышевском приближении для полинома 1-го рода 1-го порядка  это соответствует искривлению линии и пересечению ею оси x в стороне от нуля (рис. 1.7.2).

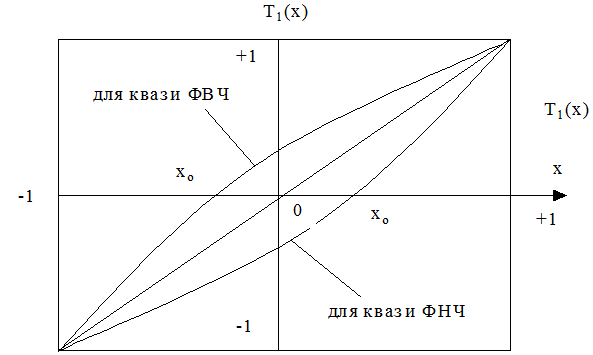
Рис. 1.7.2. Искривление линии полинома трёхэлементного контура

   Аппроксимируя эти кривые квадратной параболой по трём точкам, получим выражение для модифицированного аргумента

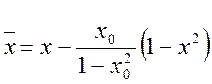                                                ,                                        (1.7.17)

где  – смещение нуля.

   Модифицированный полином 1-го порядка для квази-ФНЧ

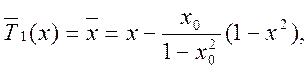                                                                          (1.7.18)

  Будем рассматривать сначала для определённости фильтры типа квази - ФНЧ (индекс LPF– от low-passfilter).

    Добротность трёхэлементного контура в  раз больше в сравнении с двухэлементным при сохранении той же резонансной частоты, которая сдвигается в сторону режекторной частоты. Введём новую ’’среднюю’’ частоту трёхэлементного контура, которую назовём опорной (basic) . Для этой частоты найдено выражение