Используя значения ![]() из (1.7.64), найдём
из (1.7.64), найдём
![]() .
(1.7. 70)
.
(1.7. 70)
Полоса ППФ - прототипа в ненормированной системе (размерность ![]() ) равна большой оси эллипса. Поэтому
ненормированное значение большой полуоси равно
) равна большой оси эллипса. Поэтому
ненормированное значение большой полуоси равно
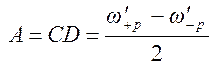 .
(1.7. 71)
.
(1.7. 71)
Сдвиг полосы ФНХ в сторону крутого ската относительно точки С
![]() .
(1.7. 72)
.
(1.7. 72)
Имея в виду (1.7.69), получим
![]() . (1.7.
73)
. (1.7.
73)
При заданной полосе ФНХ ![]() можно записать
можно записать
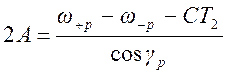 .
(1.7. 74)
.
(1.7. 74)
С учётом (1.7.70) и
(1.7.73) получаем выражение для размера большой полуоси на оси ![]()
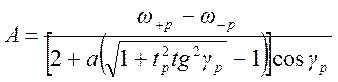 .
(1.7. 75)
.
(1.7. 75)
Критические точки К на эллипсе имеют координаты ![]() .
Из геометрических построений на рис. 1.7.6 видно, что
.
Из геометрических построений на рис. 1.7.6 видно, что
![]() (1.7.76)
(1.7.76)
где
![]() ; (1.7.77)
; (1.7.77)
![]() ;
(1.7.78)
;
(1.7.78)
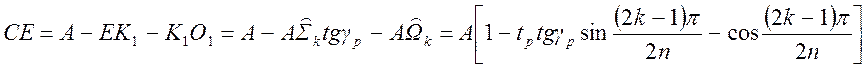 . (1.7.79)
. (1.7.79)
Подстановка этих значений в
(1.7. 76) с учётом значения ![]() из (1.7.75) даёт
из (1.7.75) даёт
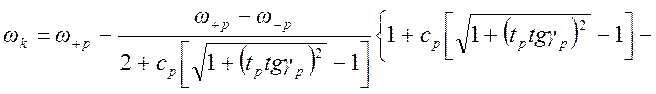
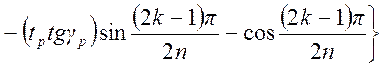 , (1.7. 80)
, (1.7. 80)
где
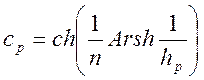 . (1.7.
81)
. (1.7.
81)
При отражении ППФ-прототипа происходит сужение полосы пропускания. Коэффициент сужения полосы прототипа
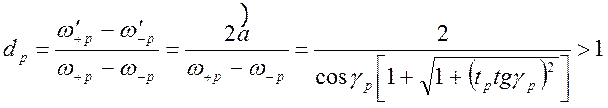 .
(1.7.82)
.
(1.7.82)
Опорная частота
получается при ![]() , т. е. при значениях
, т. е. при значениях 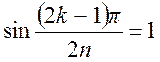 и
и 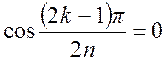 в
(1.7.80):
в
(1.7.80):
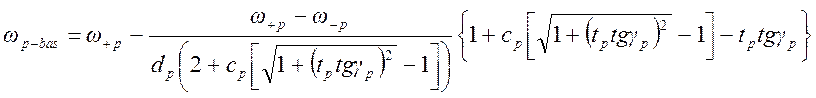 .
(1.7.83)
.
(1.7.83)
Перейдём к циклическим
частотам и обобщим полученные результаты. Для нижней полосы (индекс ![]() ) – полосы пропускания для квази-ФНЧ
или полосы заграждения для квази-ФВЧ – окончательно получим:
) – полосы пропускания для квази-ФНЧ
или полосы заграждения для квази-ФВЧ – окончательно получим:
опорная частота
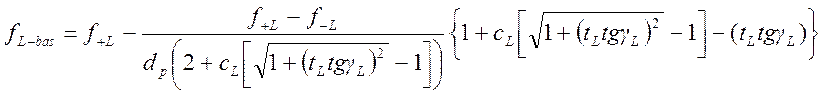 ,
(1.7.84)
,
(1.7.84)
где
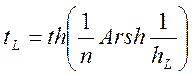 ;
(1.7.85)
;
(1.7.85)
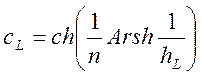 .
(1.7. 86)
.
(1.7. 86)
Критические частоты
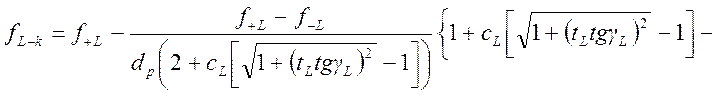
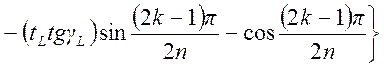 . (1.7.87)
. (1.7.87)
Нумерация частот ![]() идёт от верхних частот к нижним.
идёт от верхних частот к нижним.
Аналогично получаются выражения для частот верхней полосы (индекс) – полосы пропускания для квази-ФВЧ или полосы заграждения для квази-ФНЧ:
опорная частота
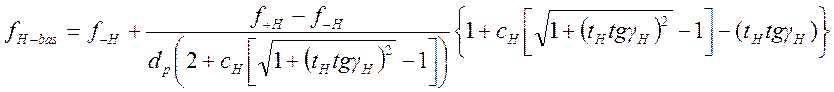 , (1.7.88)
, (1.7.88)
где
 ;
(1.7.89)
;
(1.7.89)
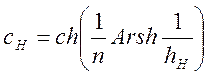 . (1.7.90)
. (1.7.90)
Критические частоты
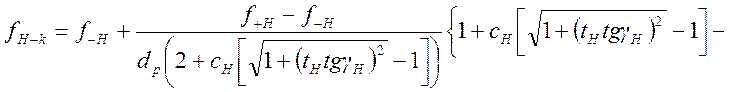
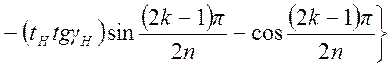 . (1.7.91)
. (1.7.91)
Здесь нумерация частот ![]() идёт от нижних частот к верхним.
идёт от нижних частот к верхним.
В формулах (1.7.84),
(1.7.87), (1.7.88), (1.7.91) коэффициент ![]() подставляется
только для полос пропускания.
подставляется
только для полос пропускания.
Если одна из критических частот в нижней полосе оказывается выше верхней
частоты ![]() или в верхней полосе оказывается
ниже нижней частоты полосы
или в верхней полосе оказывается
ниже нижней частоты полосы ![]() , то следует
ослабить требования: увеличить величину пульсаций в полосе пропускания или
уменьшить уровень затухания в полосе заграждения.
, то следует
ослабить требования: увеличить величину пульсаций в полосе пропускания или
уменьшить уровень затухания в полосе заграждения.
Если это не допускается, то увеличивается порядок фильтра ![]() .
.
Функция рабочего затухания ФНХ должна по структуре соответствовать функции
трёхэлементного контура и давать предельные переходы к чебышевскому ППФ при ![]() и инверсному чебышевскому ПЗФ при
и инверсному чебышевскому ПЗФ при ![]() для квази - ФНЧ и к ППФ при
для квази - ФНЧ и к ППФ при ![]() и к ПЗФ при
и к ПЗФ при ![]() для
квази - ФВЧ. Поэтому рабочее затухание записываем в виде
для
квази - ФВЧ. Поэтому рабочее затухание записываем в виде
![]() . (1.7.92)
. (1.7.92)
Для нахождения требуемого числа контуров при заданных функциях рабочего затухания
![]() (1.7.93)
(1.7.93)
и
![]() (1.7.94)
(1.7.94)
запишем выражения (1.7.93), (1.7.94) на граничных частотах. Для квази - ФНЧ на границе полосы пропускания
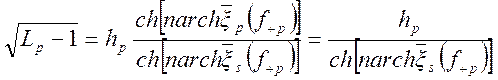 ; (1.7.95)
; (1.7.95)
на границе полосы заграждения
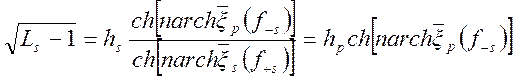 . (1.7.96)
. (1.7.96)
Поделив (1.7.94) на (1.7.95), получим для квази - ФНЧ
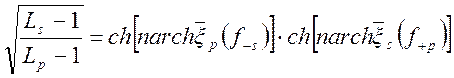 . (1.7.97)
. (1.7.97)
Аналогично для квази - ФВЧ
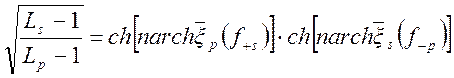 . (1.7.98)
. (1.7.98)
Из формулы (1.7.97) или (1.7.98) находится значение n и берётся ближайшее большее целое.
По
найденному n при заданном ![]() по формулам или таблицам из [7, 8] находятся
параметры низкочастотного прототипа
по формулам или таблицам из [7, 8] находятся
параметры низкочастотного прототипа ![]() .
.
Нормированные значения добротностей контуров ППФ - прототипа
![]() . (1.7.99)
. (1.7.99)
Нагруженные добротности контуров ППФ - прототипа
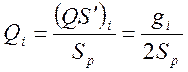 .
(1.7.100)
.
(1.7.100)
Частотный множитель ![]() для
нижней полосы пропускания (квази-ФНЧ) рассчитывается по формуле
для
нижней полосы пропускания (квази-ФНЧ) рассчитывается по формуле
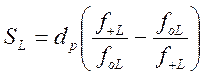 .
(1.7.101)
.
(1.7.101)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.