где
![]() – максимально допустимый коэффициент
отражения в полосе пропускания,
– максимально допустимый коэффициент
отражения в полосе пропускания, ![]() – функция
рабочего затухания, аp [дБ] - рабочее
затухание (считаем
– функция
рабочего затухания, аp [дБ] - рабочее
затухание (считаем ![]() ). Связь между аp [дБ],
). Связь между аp [дБ], ![]() и
и ![]() :
:
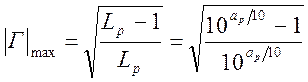 . (1.7.47)
. (1.7.47)
Если коэффициент отражения выражать в логарифмической мере
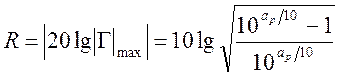 , дБ, (1.7.48)
, дБ, (1.7.48)
то амплитудный множитель равен
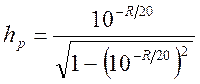 . (1.7.49)
. (1.7.49)
При
чебышевской характеристике в полосе режекции амплитудный множитель ![]() по аналогии с формулой (1.7.48) запишется как
по аналогии с формулой (1.7.48) запишется как
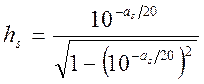 , (1.7.50)
, (1.7.50)
где
![]() – заданный уровень затухания в
полосе заграждения (считаем здесь
– заданный уровень затухания в
полосе заграждения (считаем здесь ![]() ).
).
Большая и малая полуоси эллипса в обоих случаях равны соответственно
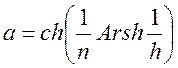 ;
(1.7.51)
;
(1.7.51)
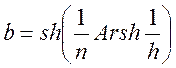 .
(1.7.52)
.
(1.7.52)
Отметим, что в чебышевском ППФ малая ось тем больше, чем меньше уровень
пульсаций ![]() ; в ПЗФ чем больше уровень
допустимого затухания
; в ПЗФ чем больше уровень
допустимого затухания ![]() , тем более узкий эллипс.
, тем более узкий эллипс.
Координаты критических точек на эллипсе
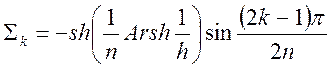 ; (1.7.53)
; (1.7.53)
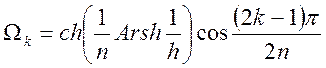 . (1.7.54)
. (1.7.54)
Нули (полюсы) расположены в левой полуплоскости, поэтому значения ![]() всегда отрицательны. В дальнейшем,
чтобы избежать путаницы со знаками, будем всегда считать
всегда отрицательны. В дальнейшем,
чтобы избежать путаницы со знаками, будем всегда считать ![]() положительными.
положительными.
У ФНХ критические частоты группируются около крутого ската, т. е. ’’собираются вовнутрь’’ характеристики. У квази - ФНЧ нули сдвинуты в высокочастотную область ПП, а полюса – в нижнюю область ПЗ. У квази - ФВЧ наоборот.
Геометрический образ ФНХ на комплексной плоскости будет иметь два характеристических эллипса, соответствующих полосам пропускания и режекции (заграждения). Оси обоих эллипсов наклонены к осям системы координат ФНХ. Большие оси эллипсов поворачиваются вокруг вершин, расположенных около крутого ската. Повороты эллипсов ПП и ПЗ осуществляются в разные стороны (рис. 1.7.5).
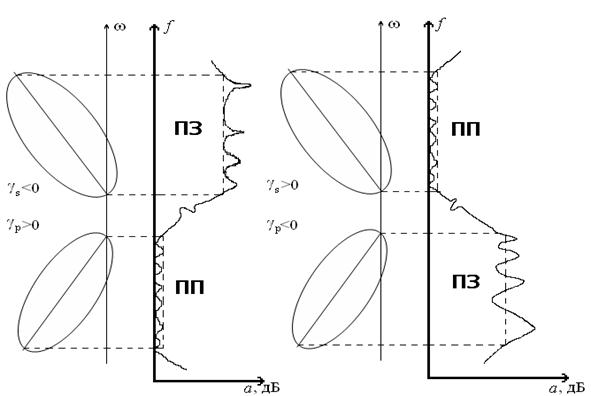
а б
Рис. 1.7.5. Фильтры с несимметричными характеристиками
на комплексной плоскости: а– квази-ФНЧ, б– квази-ФВЧ
Будем рассматривать три системы координат (рис. 1.7.5): систему ![]() , соответствующую синтезируемому ФНХ;
систему
, соответствующую синтезируемому ФНХ;
систему ![]() прототипного ППФ с симметричной АЧХ
и систему прототипа – ФНЧ
прототипного ППФ с симметричной АЧХ
и систему прототипа – ФНЧ ![]() с центром,
расположенным в середине полосы ППФ - прототипа.
с центром,
расположенным в середине полосы ППФ - прототипа.
В дальнейшем в качестве прототипа используется чебышевский ППФ, хотя все рассуждения можно отнести и к баттервортовскому фильтру, являющемуся вырожденным случаем чебышевского.
На примере нижней полосы, т.е. полосы пропускания квази - ФНЧ, найдём полосу пропускания прототипа и критические частоты ФНХ.
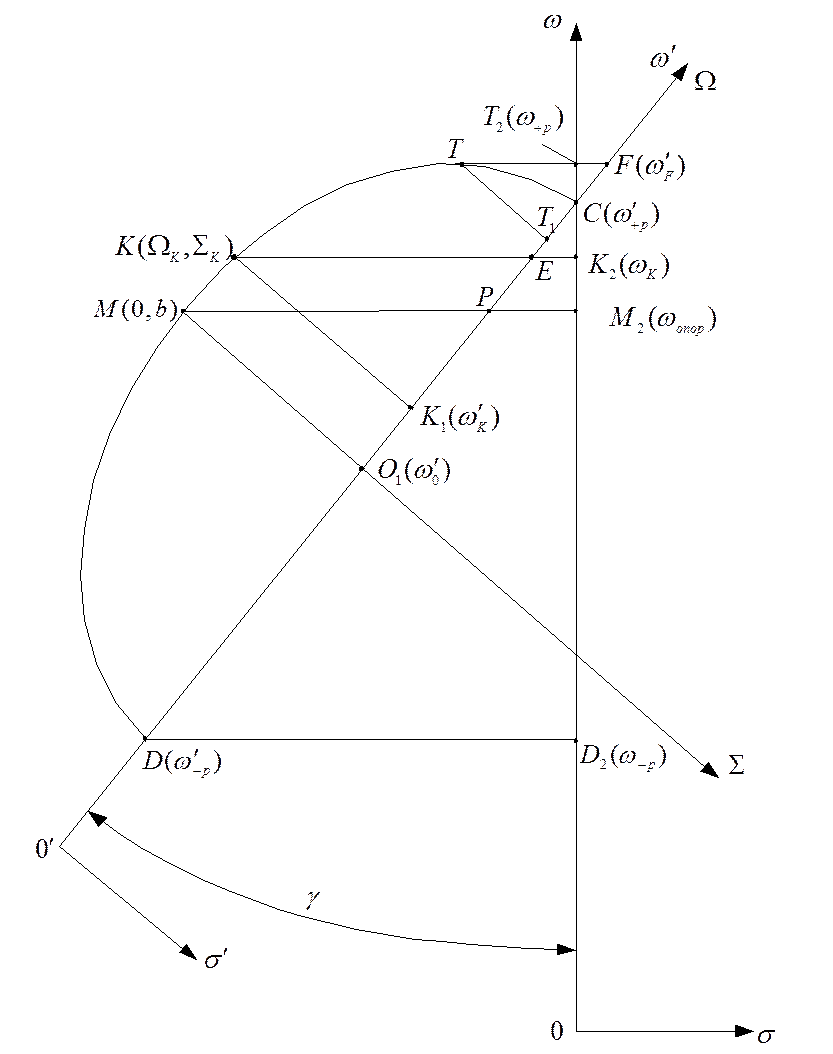
Рис. 1.7.6. Отражение координат при синтезе ФНХ (нижняя полоса)
При
введении полюсов эллипс ППФ - прототипа поворачивается на угол ![]() вокруг вершины эллипса С,
прилегающей к крутому скату (рис. 1.7.6). Системы
вокруг вершины эллипса С,
прилегающей к крутому скату (рис. 1.7.6). Системы ![]() и
и
![]() выбираются так, что
выбираются так, что ![]() , где
, где ![]() и
и
![]() – начала координат в этих системах.
– начала координат в этих системах.
Уравнение
эллипса в системе ![]()
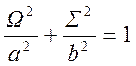 , (1.7.55)
, (1.7.55)
где a и b – большая и малая полуоси.
Для нормированного ФНЧ полоса пропускания лежит в интервале (0, 1). Нормированная частота ФНЧ связана с параметрами эллипса
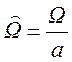 .
(1.7.56)
.
(1.7.56)
Считаем заданной полосу ФНХ ![]() . Связь частот
ППФ - прототипа и нормированного ФНЧ определяется формулой частотного
преобразования [18, 25]:
. Связь частот
ППФ - прототипа и нормированного ФНЧ определяется формулой частотного
преобразования [18, 25]:
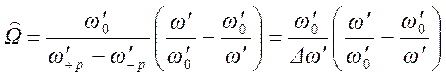 , (1.7.57)
, (1.7.57)
где центральная частота ППФ - прототипа
![]() . (1.7.58)
. (1.7.58)
Для критических частот
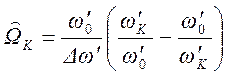 .
(1.7. 59)
.
(1.7. 59)
Отсюда получается квадратное уравнение
![]() .
(1.7. 60)
.
(1.7. 60)
Решение этого уравнения
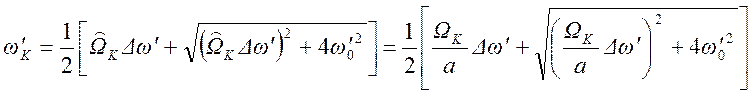 . (1.7. 61)
. (1.7. 61)
Для
не очень широкополосных фильтров (![]() ) можно
использовать упрощенное выражение
) можно
использовать упрощенное выражение
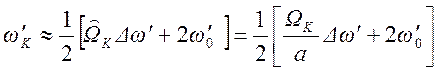 .
(1.7. 62)
.
(1.7. 62)
Верхняя частота полосы ФНХ (точка ![]() на рис. 1.7.6)
определяется касательной к эллипсу, перпендикулярной оси
на рис. 1.7.6)
определяется касательной к эллипсу, перпендикулярной оси ![]() (линия
(линия ![]() ).
).
Уравнение касательной
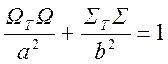 .
(1.7. 63)
.
(1.7. 63)
Отсюда при ![]() (т. е. на оси
(т. е. на оси ![]() ) в точке
) в точке ![]() имеем
имеем
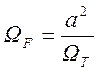 .
(1.7.64)
.
(1.7.64)
В
нормированной системе ![]() большая полуось
большая полуось ![]() . Малая полуось равна
. Малая полуось равна
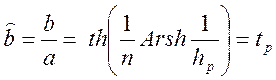 , (1.7.
65)
, (1.7.
65)
где для краткости обозначено
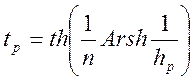 .
(1.7. 66)
.
(1.7. 66)
Из треугольника ![]() имеем
имеем
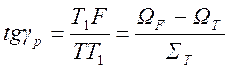 ,
(1.7. 67)
,
(1.7. 67)
откуда
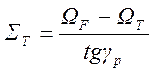 . (1.7.
68)
. (1.7.
68)
Подставим значение ![]() из (1.7.68) в уравнение эллипса
(1.7.55) для точки Т
из (1.7.68) в уравнение эллипса
(1.7.55) для точки Т
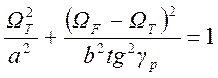 . (1.7.
69)
. (1.7.
69)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.