![]() , (1.7.19)
, (1.7.19)
где для трёхэлементного контура
![]() . (1.7.
20)
. (1.7.
20)
Эти рассуждения справедливы и для многозвенных фильтров, т. е. полиномов Чебышева высших порядков, характеристики которых уплотняются в сторону полосы режекции (рис. 1.7.3).
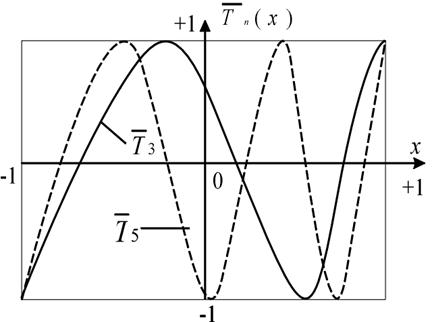
Рис. 1.7.3. Графики модифицированных полиномов Чебышева
В многозвенных фильтрах структура выражения для
опорной частоты должна быть подобна (1.7.20), но надо учесть и ширину полос пропускания
и режекции. Поэтому множитель ![]() принимает вид
принимает вид
![]() , (1.7.21)
, (1.7.21)
где перекрёстный частотный множитель
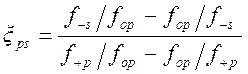 . (1.7.22)
. (1.7.22)
Модифицированный аргумент полиномов
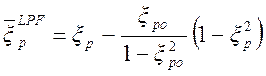 , (1.7.23)
, (1.7.23)
где частотный множитель на
опорной частоте – значение аргумента, аналогичное ![]() на
рис. 1.7.2:
на
рис. 1.7.2:
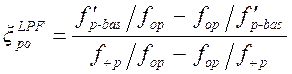 .
(1.7.24)
.
(1.7.24)
Модифицированный полином Чебышева в полосе пропускания
![]() . (1.7.25)
. (1.7.25)
Этот
полином Чебышева достигает нулей при углах ![]() .
Для нечётных полиномов центральному нулю отвечает угол 900. Угол,
соответствующий значению
.
Для нечётных полиномов центральному нулю отвечает угол 900. Угол,
соответствующий значению ![]() , или (что то же)
опорной частоте, равен
, или (что то же)
опорной частоте, равен
![]() .
(1.7.26)
.
(1.7.26)
Соответственно в полосе режекции
![]() , (1.7.27)
, (1.7.27)
где
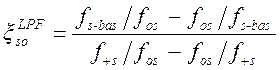 . (1.7.28)
. (1.7.28)
Назовём углы ![]() ,
, ![]() углами
асимметрии. Обобщая, можно записать окончательно для нижней полосы ФНХ (полоса
пропускания – ПП для квази - ФНЧ или полоса режекции – ПЗ для квази - ФВЧ –
индекс «L»)
углами
асимметрии. Обобщая, можно записать окончательно для нижней полосы ФНХ (полоса
пропускания – ПП для квази - ФНЧ или полоса режекции – ПЗ для квази - ФВЧ –
индекс «L»)
![]() ,
(1.7.29)
,
(1.7.29)
где
![]() ;
(1.7.30)
;
(1.7.30)
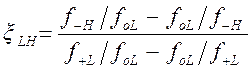 .
(1.7.31)
.
(1.7.31)
Здесь индекс «Н» обозначает верхнюю полосу – ПП для квази-ФВЧ или ПЗ для квази-ФНЧ.
Частотные переменные
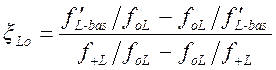 ;
(1.7.32)
;
(1.7.32)
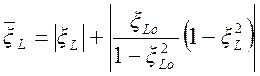 . (1.7.33)
. (1.7.33)
Модули
берутся для того, чтобы по обе стороны от частоты ![]() частотные
переменные были положительными.
частотные
переменные были положительными.
Текущее значение частотной переменной
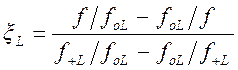 .
(1.7.34)
.
(1.7.34)
Угол асимметрии
![]() .
(1.7.35)
.
(1.7.35)
Обозначения частот даны на рис. 1.7.4.

![]()
а б
Рис.1.7.4. Обозначение частот ФНХ: а–нижняя полоса; б–верхняя полоса
![]() и
и ![]() –
среднегеометрические частоты;
–
среднегеометрические частоты; ![]() и
и ![]() – среднеарифметические частоты
– среднеарифметические частоты
Для верхней полосы (ПП для квази - ФВЧ или ПЗ для квази - ФНЧ)
![]() ,
(1.7.36)
,
(1.7.36)
где
![]() .
(1.7.37)
.
(1.7.37)
У обычного двухэлементного
контура (пропускающего и режекторного) высокочастотный скат менее крутой по
сравнению с низкочастотным. Отношение верхней полуполосы (![]() ) к нижней полуполосе (
) к нижней полуполосе (![]() ) всегда больше единицы:
) всегда больше единицы:
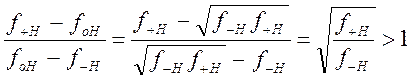 . (1.7.38)
. (1.7.38)
При этом верхняя полоса
оказывается вытянутой в сторону верхних частот. Поэтому взаимную нормированную
частотную ![]() переменную умножаем на коэффициент
(1.7.38):
переменную умножаем на коэффициент
(1.7.38):
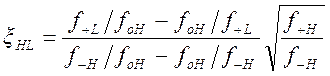 ; (1.7.39)
; (1.7.39)
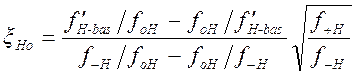 ;
(1.7.40)
;
(1.7.40)
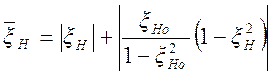 ; (1.7.41)
; (1.7.41)
Значение ![]() всегда отрицательно.
всегда отрицательно.
Угол асимметрии
![]() . (1.7.42)
. (1.7.42)
1.7.2. Геометрический образ фильтра
Переходу от прототипного чебышевского ППФ к ФНХ можно дать простую геометрическую интерпретацию.
В симметричном чебышевском фильтре, как известно [25, 26], критические точки –
нули функции фильтрации ![]() для
полосно-пропускающего фильтра (ППФ) и полюсы для полосно-заграждающего
(режекторного) фильтра ПЗФ расположены на характеристическом эллипсе в
плоскости нормированной комплексной частоты
для
полосно-пропускающего фильтра (ППФ) и полюсы для полосно-заграждающего
(режекторного) фильтра ПЗФ расположены на характеристическом эллипсе в
плоскости нормированной комплексной частоты ![]() .
Критические точки разнесены на угол
.
Критические точки разнесены на угол
![]()
![]() ,
(1.7. 43)
,
(1.7. 43)
где n – порядок фильтра (число контуров).
В нормированном виде (большая ось эллипса лежит в интервале ![]() ) эллипс описывается уравнением [25, 26]
) эллипс описывается уравнением [25, 26]
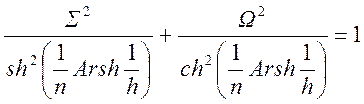 ,
(1.7. 44)
,
(1.7. 44)
где h – амплитудный множитель. Для ППФ он равен [7]
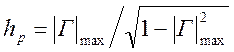 (1.7.
45)
(1.7.
45)
или
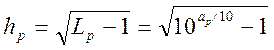 , (1.7. 46)
, (1.7. 46)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.