Синтез фильтров с несимметричными частотными характеристиками методом отражения координат, страница 5

Частотный множитель   для верхней полосы пропускания (квази-ФВЧ):

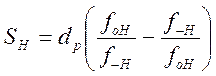                                                    .                                   (1.7.102)                                           

Эти значения подставляются в формулу для определения добротностей пропускания контуров

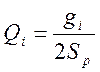                                                           ,                                            (1.7.103)

где –  параметры низкочастотного прототипа [8, 17].

    Распределение частот режекции по контурам в принципе произвольное, но, как показывает опыт, лучше  режекторные частоты, наиболее близкие к полосе пропускания, помещать в контуры с большей добротностью, обычно это  внутренние контуры фильтра. При этом можно получить меньшие пульсации в полосе пропускания.

После распределения добротностей и режекторных частот по контурам можно найти значения L, C  элементов.

Таблица 1.7.3.  Формулы для расчёта элементов ФНХ

Схема	Нормированные параметры
Квази-ФНЧ ,	; ;
Квази-ФНЧ ,	; ;

                                                                                           Табл. 1.7.3. Окончание

В табл. 1.7.3 приведены формулы для определения нормированных по частоте  (формула (1.7.84) или (1.7.88)) значений элементов при одинаковых значениях сопротивлений нагрузок R  на входе и выходе фильтра.

Лестничная схема трёхзвенного фильтра на трёхэлементных контурах показана на рис.1.7.7, а типичная АЧХ такого фильтра – на рис. 1.7.8 .

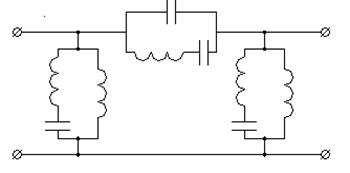
Рис. 1.7.7. Лестничная схема ФНХ

            Следует отметить, что рассмотренный метод синтеза является приближённым. Поэтому при расчёте следует брать полосы пропускания и заграждения с запасом, причём «напуск» на полосу следует делать главным образом на частоты, примыкающие к переходной зоне между полосами пропускания и заграждения. Погрешность метода растёт с уменьшением интервала между полосами пропускания и заграждения. При ширине интервала между полосами менее 3 процентов обычно приходится немного сдвигать опорную частоту в полосе пропускания в сторону полосы заграждения.

Проектирование ФНХ желательно вести с помощью любой программы анализа электронных схем. Если частотная характеристика оказалась не удовлетворительной, то следует провести расчёт во втором приближении. Для этого найденная по формулам  (1.7.84) или (1.7.88) опорная частота подставляется в формулу (1.7.35) или (1.7.42) и находятся новые значения углов   и  . Далее расчёт ведётся по приведённой методике.

Для проверки предложенного синтеза были просчитаны фильтры, частотный план которых показан на рис. 1.7.9. Проверялись фильтры квази-ФНЧ и квази - ФВЧ. Кроме соответствия заданию полученных полос пропускания и заграждения (по частотам и уровням затухания) контролем служило совпадение нулей затухания в полосе пропускания со значениями, рассчитанными по формулам (1.7.87), (1.7.91).

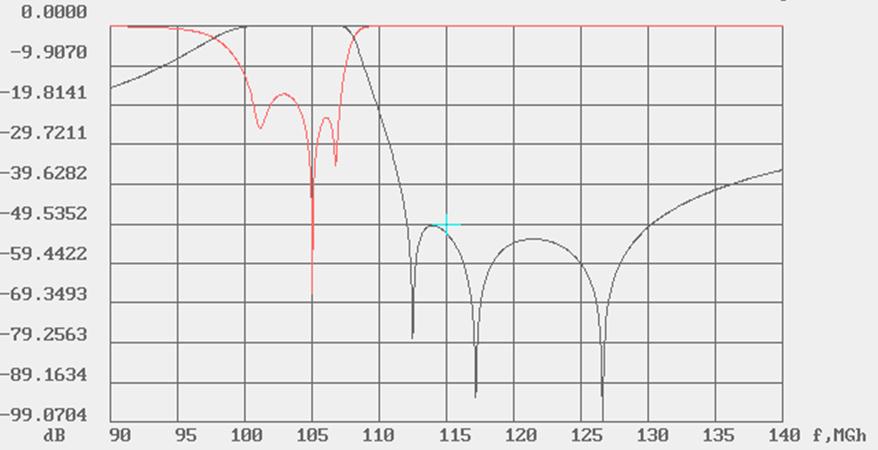
Рис. 1.7.8. Пример частотной характеристики трёхзвенного квази-ФНЧ

Рис. 1.7.9. Частотный план рассчитанных фильтров

Фильтры на трёхэлементных контурах могут быть использованы в низкочастотной области, но здесь обязательно следует учитывать паразитные параметры – ёмкость катушек и потери в конденсаторах и катушках, которые могут в ряде случаев кардинально исказить характеристики. Учёт этих эффектов и методы  компенсации содержатся, например, в [29, 30].

1.7.3. Порядок расчёта ФНХ

Заданы полосы пропускания    и заграждения    и потери в них [дБ]. Считаем .

При расчётах удерживать количество значащих цифр не менее n.

1. По формулам (1.3.9) и (1.3.10) находим функции рабочего затухания , а затем по формулам (1.7.46), (1.7.50) определяются амплитудные множители  .

2.  Средне-геометрические частоты  ,  [формулы (1.7.15), (1.7.16)].

3. Находим перекрёстные  нормированные частотные переменные   (1.7.31),  (1.7.39).

4. Рассчитываем  коэффициенты  и  по формулам (1.7.30), (1.7.37).

5. Определяем опорные частоты в первом приближении  (1.7.29), (1.7.36).

6. Вычисляем частотные переменные на опорных частотах  (1.7.32),    (1.7.40). 

7.  Находим углы асимметрии  (1.7.35),  (1.7.42).

8. Определяем требуемое количество контуров n по формуле (1.7.97) или (1.7.98).

9. Рассчитываем коэффициент сужения полосы прототипа  по формуле (1.7.82).

10. Отношение  размеров осей эллипсов ,  рассчитываем по формулам (1.7.85), (1.7.89), значения   и  соответственно по формулам (1.7.86), (1.7.90).

11. Находим критические  частоты по  (1.7.87) или (1.7.91) и опорные частоты во втором приближении по (1.7.84) или (1.7.88).  Значения  частот нулей при дальнейших расчётах не требуются,  они могут быть использованы как контрольные.

12. По заданному значению   из таблиц или по формулам  [6,  7]     находятся  нормированные значения параметров прототипа     и нормированные значения добротностей  по формуле  (1.7.99).

13. Частотный множитель  для квази-ФНЧ  определяем по формуле (1.7.101),   для квази-ФВЧ – по формуле (1.7.102). 

14.  Рассчитываем нагруженные добротности контуров (1.7. 103).

15. Распределяем режекторные частоты по контурам и при выбранной лестничной структуре ФНХ  по формулам табл. 1.7.3 находим нормированные по частоте    второго приближения  (1.7.84),  (1.7.88)  значения элементов L, C.

Истинные значения элементов L,C  находятся путём ренормирования.

Использование рассмотренной методики при синтезе СВЧ фильтров  описано в гл. 3.