Радиоавтоматика: Учебное пособие для практических занятий, страница 7

Оптимизация системы по шумовой полосе сводится к нахождению оптимального значения K, при котором минимизируется (24.6). В общем случае выражение для K_опт представить невозможно (один из способов решения задачи графический). Однако для случая высокой точности слежения, когда K>>w_д и K>>w_н формула для оптимальной полосы F_ш принимает вид

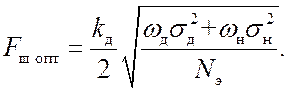
Чем больше дисперсия (мощность) частотных флуктуации F_Д(t) и df_г(t) и чем шире их спектры w_д и w_н, тем более широкая полоса требуется для слежения с минимально достижимой ошибкой.  

Пример 25

Произвести выбор структуры ФНЧ и параметров системы ФАПЧ, обеспечивающих заданные показатели качества: быстродействие t_п0,1с; перерегулирование e£30%, фазовую ошибку j£p/20 рад  при ускорении =20p рад/с².

Решение

По заданному времени переходного процесса находим частоту среза разомкнутой системы: w_ср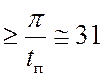с^–1. Выбираем значение w_ср=40с^–1.

При выборе структуры ФНЧ учитываем, что система должна обеспечить постоянную фазовую ошибку по ускорению (обладать астатизмом второго порядка). Кроме того, ЛАХ разомкнутой системы на частоте среза должна иметь наклон –20дБ/дек (протяженность участка ЛАХ с таким наклоном должна составлять декаду и более). Это гарантирует необходимый запас устойчивости и требуемое качество переходного процесса. Для эффективного подавления шумов наклон ЛАХ в области верхних частот должен составлять не менее – 40дБ/дек (см. п. 5).

Указанным требованиям удовлетворяет типовая ЛАХ, представленная на рис. 25.1.  Она  соответствует  ФНЧ  с  передаточной  функцией

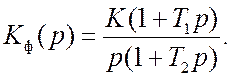
Рис. 25.1

Выбираем частоты сопряжения: и , что соответствует постоянным времени Т₁=0,1c и Т₂=0,01с.

Заданному перерегулированию e30% соответствует показатель колебательности АЧХ замкнутой системы М1,5, что достигается при отношении w_cр/w₀³1,7 (см. лекцию 10), то есть значении собственной частоты системы

w₀=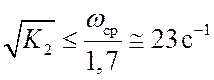 (выбираем ).

Усиление разомкнутой системы (добротность по ускорению)

K₂=2pk_Дk_гK=w₀²=.

Запас устойчивости по фазе равен

j=p–|j_р(w_ср)|=

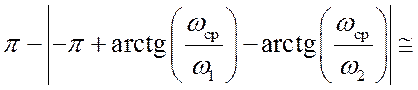
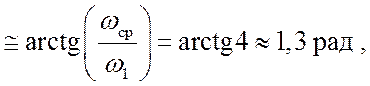
что является приемлемым (запас по усилению определять не требуется, так как ФЧХ не пересекает линию –p рад). 

Динамическая ошибка системы второго порядка астатизма равна (см. лекцию 11) 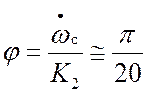 рад, что удовлетворяет требованиям.

Пример 26

Для системы ФАПЧ, представленной структурной схемой на рис. 26.1 (синтезатор частот), произвести оптимизацию шумовой полосы по параметру K₂, используя критерий минимума дисперсии фазового шума на выходе. Фазовый шум dj₀(t) опорного генератора полагается белым со спектральной плотностью N₀, а фазовый шум d_jг(t) подстраиваемого генератора имеет спектральную плотность N_jг/w².

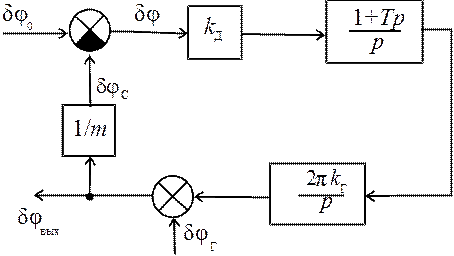
Рис. 26.1

Решение

По заданной структурной схеме находим передаточную функцию замкнутой системы:

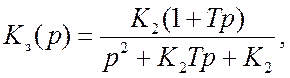
где K₂=2pk_дk_г – добротность системы по ускорению.

Шумовая полоса системы равна (см. п. 5)

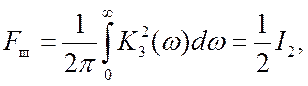
где I₂ – табличный интеграл, a полиномы

A₂(jw)=(jw)²+K₂T(jw)+K₂,

B₂(w)=

Учитывая, что коэффициенты a₀=1; а₁=K₂Т; а₂=K₂; b₀=Т²; b₁=K₂², находим

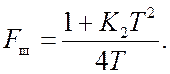
Дисперсия составляющей фазового шума, обусловленной шумом опорного генератора, определяется выражением

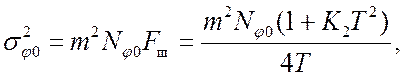
так как передаточная функция от «d_j0 к d_jвых» равна mK_з(р).

Дисперсия составляющей фазового шума, обусловленной шумом подстраиваемого генератора, равна

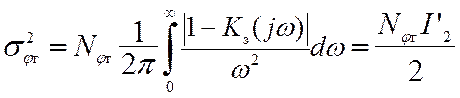
где          

     

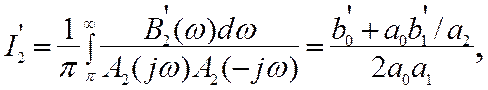
а полином В₂'(w)=w² (b₀'=1, b₁'=0).

Отсюда с учётом значений коэффициентов а₀=1, а₁=K₂Т и а₂=K₂ находим

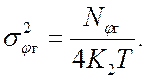
Оптимизация системы по параметру K₂ в соответствии с критерием минимума дисперсии фазового шума

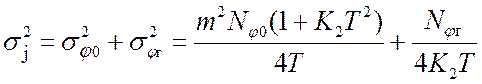
сводится к дифференцированию s_j² по K₂ и приравниванию производной к нулю. В результате получаем

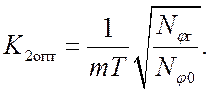
Оптимальная шумовая полоса

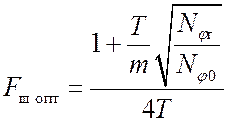
определяется отношением энергетических спектров фазовых шумов подстраиваемого и опорного генераторов.

Пример 27

Выбрать структуру ФНЧ и параметры ССЗ (рис. 27.1), обеспечивающие заданные показатели качества: шумовую полосу F_ш≤10 Гц; ошибку слежения Dt≤0,1 мкс при ускорении = 20 мкс/с².

Решение

Указанным требованиям по точности удовлетворяет система второго порядка астатизма с ФНЧ,описываемым передаточной функцией

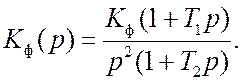
Шумовая полоса системы определяется выражением (см. п. 5)

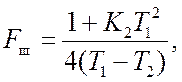                                   (27.1)

где K₂ =k_дk_рK_ф – добротность по ускорению.

По заданной динамической ошибке находим требуемое значение K₂:

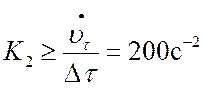 (выбираем ).

          Полагая Т₁=10Т₂, что гарантирует хорошее качество переходного процесса (см. пример 25), перепишем (27.1) в виде

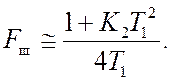                                          (27.2)

По заданной полосе F_ш и выбранном значении K₂ из (27.2) находим постоянную времени Т₁0,12с (решая квадратное уравнение). Постоянная    Т₂ =Т₁/10 0,012с.

Используя ЛАХ разомкнутой системы (см. лекцию 7), определяем частоту среза w_ср из уравнения

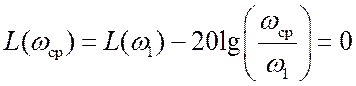
или              

     ,

 где  Отсюда w_ср=w₀²T₁@30c^–1.

Запас устойчивости по фазе равен

          j@arctg(w_срТ₁)@ arctg(3,6)@ 70^°,

а запас по усилению определять не требуется (ЛФХ не пересекает прямой j(w)= –p).

Для косвенной оценки качества переходного процесса находим отношением w_ср/w₀@2, что гарантирует перерегулирование e<30% (см. лекцию 11).

Пример 28

Для ССН, представленной структурной схемой на рис. 28.1, а, определить параметр K₁=k_дK, при котором обеспечиваются заданные показатели качества: быстродействие t_п£2с, перерегулирование e = 0; угловая ошибка a_д£2 град при скорости u_a= 3 град/с.

Решение

Рассматриваемая система (в разомкнутом состоянии) имеет ЛАХ вида (рис. 28.1, б).

Частоту среза определим из условия w_ср³p/t_п@1,57 (выбираем         w_ср=1,6).

Добротность системы по скорости K₁=w_ср=1,6 .

Динамическая ошибка системы первого порядка (см. лекцию 12) равна

.

      

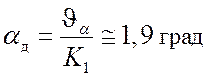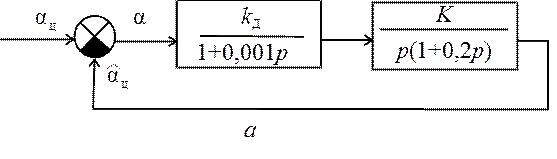
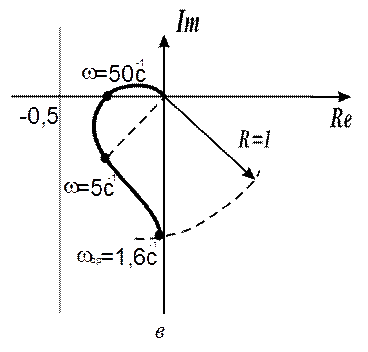
Рис. 28.1