Положительность коэффициентов а0, a1 и a2 , (необходимое условие устойчивости) обусловлена тем, что постоянные времени Т1 и T2, а также коэффициенты усиления K1 и K2 не могут быть отрицательными (или равными нулю) по своему физическому смыслу. Положительность коэффициентов характеристического уравнения определяет также и достаточное условие устойчивости, так как порядок уравнения равен двум, а минор с максимальным индексом, который необходимо вычислить, – это D1=a1>0.
Таким образом, рассмотренная замкнутая система устойчива при любых значениях параметров K1, K2, T1 и Т2 Системы такого вида называют «абсолютно устойчивыми ».
Пример 9
Провести анализ устойчивости замкнутой системы, отличающейся от рассмотренной в примере 8, лишь тем, что она содержит не один, а два интегратора с общим коэффициентом усиления K.
Решение
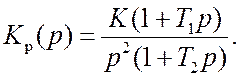(9.1)
Для передаточной функции замкнутой системы в соответствии с (8.44) можем записать
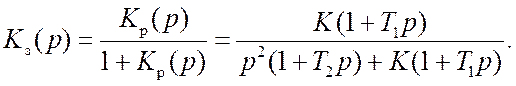(9.2)
Отсюда находим характеристическое уравнение
T2p3 +
p2 +KT1p + K=0, (9.3)
коэффициенты которого определяются как
a0=T2, a1=1, a2=KT1, a3=K. (9.4)
Необходимое условие устойчивости выполняется при любых значения параметров (по физическому смыслу все параметры положительны).
Достаточное условие устойчивости сводится к проверке неравенства
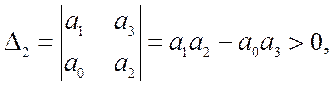(9.5)
так как условие D1= а1> 0 выполняется автоматически.
Подставив в (9.5) выражение (9.4) для коэффициентов уравнения, находим, что для устойчивой системы необходимо выполнение условия Т1>Т2 (при этом коэффициент усиления K может быть любым). Равенство постоянных времени форсирующего и инерционного звеньев соответствует системе, находящейся на границе устойчивости (такая система эквивалентна системе, состоящей из безынерционного звена и двух интеграторов, так как общий коэффициент передачи форсирующего и инерционного звеньев равен единице на всех частотах от нуля до бесконечности).
Пример 10
Определить критический коэффициент усиления для системы, содержащей безынерционное звено и три инерционных звена с постоянными времени Т1, Т2 ,Т3.
Решение
Характеристическое уравнение замкнутой системы в данном случае имеет вид
(10.1)
где
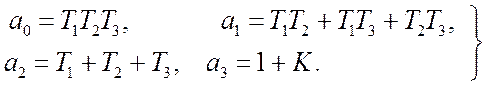(10.2)
(K– общее усиление разомкнутой системы).
Критическое значение коэффициента усиления можно определить на основании критерия Гурвица, полагая
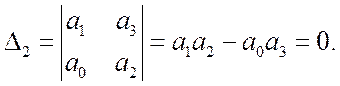(10.3)
Подставив в (10.3) значения коэффициентов (10.2), получим
После алгебраических преобразований (раскрывая скобки и поделив на значение a0) запишем
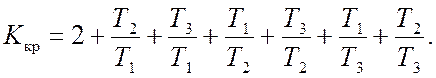(10.4)
Из (10.4) можно сделать весьма важный практический вывод: критический коэффициент усиления является функцией отношения постоянных времени. Изменяя это отношение, можно в достаточно широких приделах получать значения Kкр. Например, при Т1=Т2=Т3=Т имеем Kкр=8 независимо от величины 0<T< µ (заметим, что системы, не содержащие интегрирующих звеньев, называются статическими).
Для заданной структурной схемы (рис. 29.1) построить ЛАХ и ЛФХ разомкнутой системы. Определить запас устойчивости по фазе и усилению при k0 = 0,01; k1 = 10 с-1.
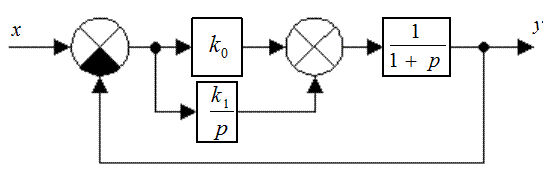
Рис. 29.1
Выбрать значение параметра Т, при котором обеспечивается приемлемый запас устойчивости системы (рис. 30.1).
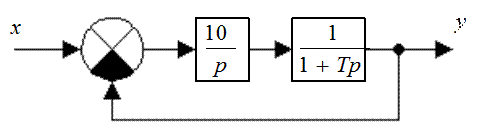
Рис. 30.1
Передаточная функция разомкнутой системы
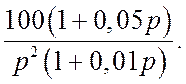
Определить запас устойчивости для замкнутой системы.
Передаточная функция разомкнутой системы
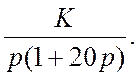
Выбрать значение параметра K, обеспечивающее приемлемый запас устойчивости для замкнутой системы
Передаточная функция разомкнутой системы
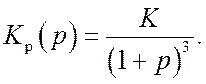
Найти значение параметра Kиз условия, что запас пофазе для замкнутой системы Dj³ π/4 рад, а запас по усилениюррррара DL³ 6дБ.
Занятие 5. Устойчивость замкнутых автоматических
систем
Пример 11
Провести анализ устойчивости замкнутой системы, состоящей из типовых звеньев: двух интегрирующих (с общим коэффициентом передачи kи =104 с–2), инерционного и форсирующего (постоянные времени соответственно равны 0,002 с и 0,05 с, а коэффициенты передачи – единице).
Решение
Определяем частоты сопряжения асимптот ЛАХ форсирующего и инерционного звеньев, а также частоту среза двух интеграторов (считая их одним звеном с передаточной функцией kи/p2):
С учетом этих данных строим логарифмические частотные характеристики разомкнутой системы (рис. 11.1). ЛАХ разомкнутой системы состоит из трех асимптот: 1 и 3 с наклоном – 40 дБ/дек и 2 – с наклоном – 20 дБ/дек. ЛФХ системы не пересекает уровень – p рад, поэтому замкнутая система устойчива. Запас устойчивости по фазе составляет приблизительно p/4 рад, а запас по усилению не имеет смысла определять (теоретически он бесконечен, так как ЛФХ достигает – p рад лишь в асимптотических точках w®0 и w®¥).
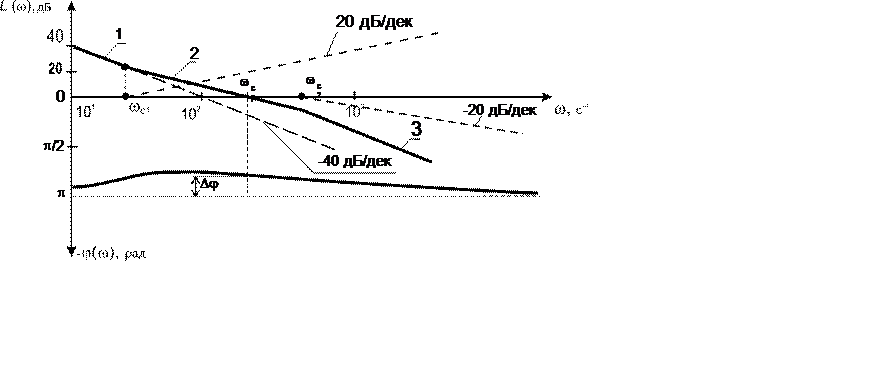
Рис. 11.1
Пример 12
Провести анализ устойчивости замкнутой системы, состоящей из двух интегрирующих звеньев и инерционного звена с постоянной времени Т.
Решение
Используя критерий Найквиста, убеждаемся, что система такого типа неустойчива при любых значениях параметров K (общее усиление разомкнутой системы) и Т (рис. 12.1). На рис. 12.1, а представлены АФХ системы для двух значений коэффициента усиления: K (кривая 1) и 2K (кривая 2) при Т =const. Рис. 12.1, б иллюстрирует влияние постоянной времени на форму АФХ при K = const (кривая 1 соответствует значению Т1, а кривая 2 – Т 2>Т1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.