Системы, устойчивость которых не может быть обеспечена надлежащим выбором параметров, называются структурно неустойчивыми.
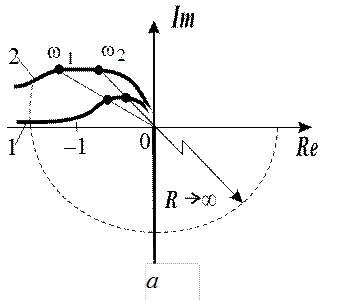
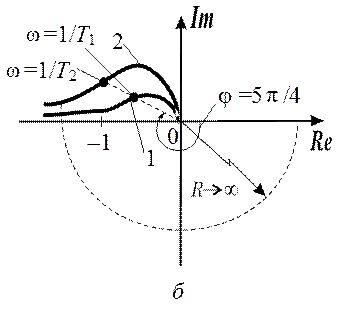
Рис. 12.1
Пример 13
Определить критическое усиление для замкнутой статической системы, состоящей из четырёх инерционных звеньев с одинаковыми постоянными времени Т.
Решение
Построимкривую АФХ (качественно, поскольку параметры K и Т не определены) для критического случая (рис. 13.1).

Рис. 13.1
Для частоты w=0 модуль АФХ равен K, а для частоты w®¥
он равен нулю (при этом фазовый сдвиг составляет 2p
рад). В силу идентичности звеньев фазовый сдвиг, вносимый каждым звеном в
отдельности на частоте среза, равен p/4 радиан, а коэффициент
передачи составляет ![]() (общее усиление K
учтем путем введения безынерционного звена). Отсюда общий коэффициент усиления
разомкнутой системы на частоте среза можно представить в виде
(общее усиление K
учтем путем введения безынерционного звена). Отсюда общий коэффициент усиления
разомкнутой системы на частоте среза можно представить в виде
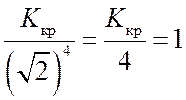
и, следовательно, Kкр=4.
Результат
справедлив для любого значения Т, так как при K=const изменение Т приводит лишь к разной скорости «закручивания
спирали» (c ростом Т уменьшается значение частоты
среза ![]() ).
).
ЛАХ разомкнутой системы имеет вид (рис. 34.1).
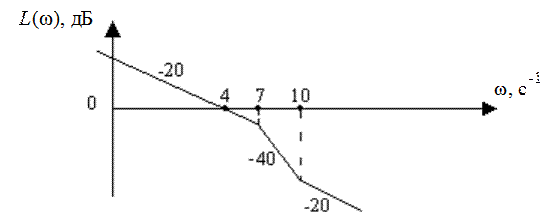
Рис. 34.1
Определить запас устойчивости замкнутой системы.
ЛАХ разомкнутой системы имеет вид (рис. 35.1).
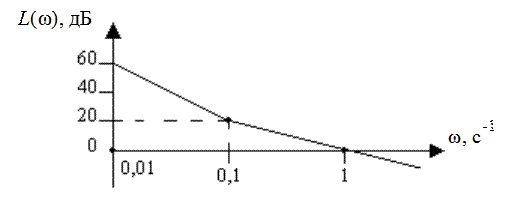
Рис. 35.1
Определить запас устойчивости замкнутой системы.
ЛАХ разомкнутой системы имеет вид (рис. 36.1).
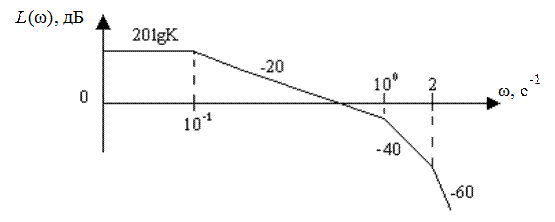
Рис. 36.1
Определить значение параметра K, при котором обеспечиваются запас устойчивости по усилению не менее 6 дБ и по фазе не менее 30 град (для замкнутой системы).
ЛАХ разомкнутой системы имеет вид (рис. 37.1).
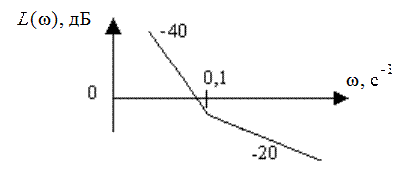
Рис. 37.1
Определить значение коэффициента усиления разомкнутой системы, при котором запас по фазе Δφ=π/6 рад (для замкнутой системы).
Занятие 6. Оценка качества переходного процесса
Пример 14
Оценить качественные показатели переходного процесса в замкнутой системе (рис. 14.1, а), используя операторный метод Лапласа.
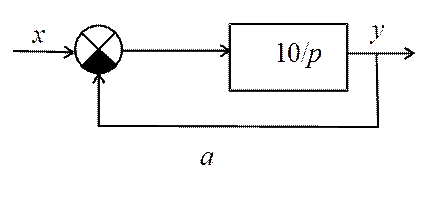
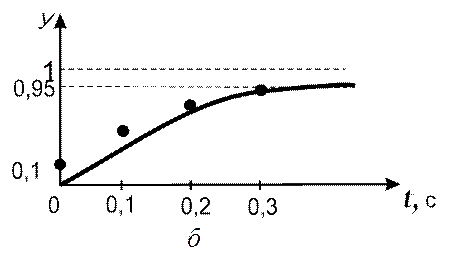
Рис. 14.1
Решение
Передаточная функция замкнутой системы равна
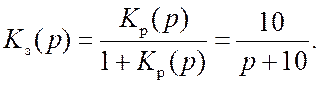
Учитывая, что изображение Лапласа от функции единичного скачка, X(p)=1/p, находим изображение управляемой переменной
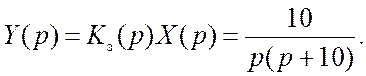
По таблице преобразований Лапласа [Приложение 1] находим оригнал,
![]()
что совпадает с переходной характеристикой инерционного звена с постоянной времени Т=0,1с.
Следовательно, переходный процесс монотонный (без перерегулирования), а длительность его tп=3Т=0,3c (рис 14.1, б).
Пример 15
Используя метод цифрового моделирования построить график переходного процесса для системы, рассмотренной в примере 14. Определить быстродействие системы.
Решение
Передаточная функция цифровой модели системы равна
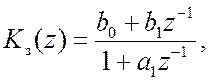
где коэффициенты разностного уравнения
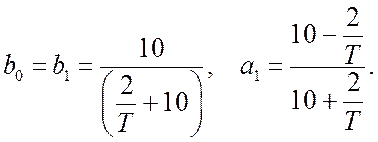
Подставив их в (10.11) (лекция 10), находим разностное уравнение
![]()
Интервал дискретизации выбираем из условия T<<![]() T1
(Т1=0,1с, а
T1
(Т1=0,1с, а ![]() с–1 –
полоса системы по уровню 0,7). Для удобства берём значение Т=0,02с; при
этом коэффициенты
с–1 –
полоса системы по уровню 0,7). Для удобства берём значение Т=0,02с; при
этом коэффициенты ![]() .
.
График переходного процесса, построенный с использованием разностного уравнения, представлен на рис. 14.1, б (сплошная кривая соответствует точному решению методом Лапласа, а точки на ней – результатам моделирования). Как видим из рисунка, расхождение невелико (не превышает 10%). Быстродействие системы составляет tП=0,3 c (15T).
Пример 16
Оценить качество переходного процесса в системе (рис. 14.1, а), используя АЧХ замкнутой системы.
Решение
Для рассматриваемой системы АЧХ ![]() может
быть найдена непосредственно по передаточной функции Kз(р)=1/(1+0,1р):
может
быть найдена непосредственно по передаточной функции Kз(р)=1/(1+0,1р):
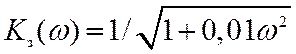 .
.
Однако с целью иллюстрации возможности применения графического метода построения АЧХ замкнутой системы по кривой АФХ разомкнутой системы воспользуемся указанным методом.
Представим АФХ разомкнутой системы в виде
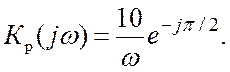
График ![]() имеет вид прямой,
совпадающей с осью ординат (рис. 16.1, а) и уходящей в
бесконечность при w® 0.
имеет вид прямой,
совпадающей с осью ординат (рис. 16.1, а) и уходящей в
бесконечность при w® 0.
Поскольку АФХ ![]() расположена
правее вертикальной линии, проходящей через точку – 0,5 на оси абсцисс, то
можно сделать вывод о том, что АЧХ замкнутой системы – убывающая функция
частоты, а переходный процесс – монотонный (без перерегулирования). Значения
расположена
правее вертикальной линии, проходящей через точку – 0,5 на оси абсцисс, то
можно сделать вывод о том, что АЧХ замкнутой системы – убывающая функция
частоты, а переходный процесс – монотонный (без перерегулирования). Значения ![]() при фиксированных w
(например, равных 2,5,10 и т. д.) находятся как отношение длин векторов:
при фиксированных w
(например, равных 2,5,10 и т. д.) находятся как отношение длин векторов: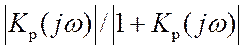 . В точках w=0
и w=¥
эти значения известны (соответственно, единица и нуль). График АЧХ (рис. 16.1, б)
позволяет оценить полосу пропускания замкнутой системы
. В точках w=0
и w=¥
эти значения известны (соответственно, единица и нуль). График АЧХ (рис. 16.1, б)
позволяет оценить полосу пропускания замкнутой системы ![]() по
уровню
по
уровню ![]() (она равна 10 с–1), а
следовательно, время переходного процесса
(она равна 10 с–1), а
следовательно, время переходного процесса ![]() .
.
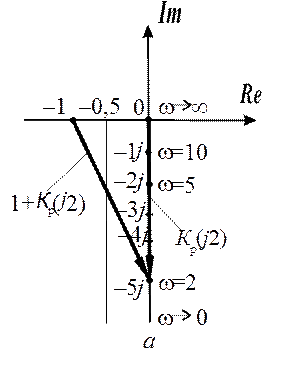
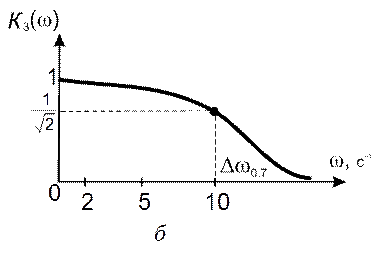
Рис. 16.1
Пример 17
Используя метод оценки качества переходного процесса по ЛАХ разомкнутой системы построить переходную характеристику при единичном воздействии для системы с передаточной функцией
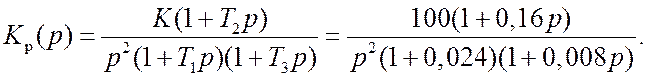
Решение
По заданной
передаточной функции строим ЛАХ разомкнутой системы (рис. 17.1, а).
Определяем ![]() и вычисляем
и вычисляем ![]() ,
а также
,
а также![]() . Протяженность участка с наклоном –
20 дБ/дек равна
. Протяженность участка с наклоном –
20 дБ/дек равна ![]() .
.
Находим отношение wср/w0=1,6 по табл. 1.2 диапазон 1,5<М<1,7. По
графику (рис. 1.51) отыскиваем некоторую универсальную кривую ![]() между М=1,5 и М=1,7.
Разделив абсциссы этой универсальной переходной характеристики на
между М=1,5 и М=1,7.
Разделив абсциссы этой универсальной переходной характеристики на ![]() , получаем переходную характеристику
для рассматриваемой системы (рис. 17.1, б). По характеристике определяем
перерегулирование
, получаем переходную характеристику
для рассматриваемой системы (рис. 17.1, б). По характеристике определяем
перерегулирование ![]() и быстродействие
и быстродействие ![]() .
.
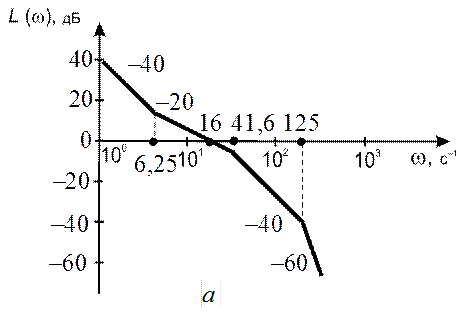
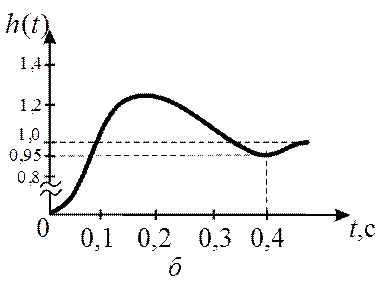
Рис. 17.1
Для замкнутой системы (рис. 38.1) найти переходную характеристику, определить быстродействие и перерегулирование при Т = 0,2 с.
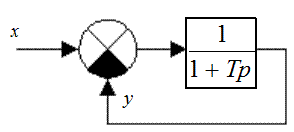
Рис. 38.1
Для замкнутой системы (рис. 39.1) определить значение параметра k, при котором обеспечивается заданное время переходного процесса: tп < 0,01с.
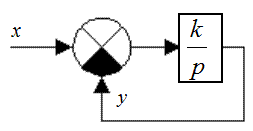
Рис. 39.1
Занятие 7. Точность действия автоматических систем
Пример 18
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.