Радиоавтоматика: Учебное пособие для практических занятий, страница 6

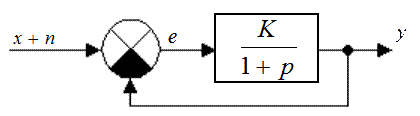
Рис. 49.1

Задача 50

Провести оптимизацию системы (рис. 50.1) по параметру K, используя критерий минимума среднего квадрата ошибки. Воздействие х(t) = 0,2 – t, а помеха – белый шум с энергетическим спектром N₀ = 0,5 Гц ^–1.

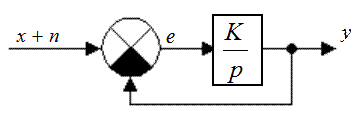
Рис. 50.1

Занятие 8. Показатели качества типовых

систем радиоавтоматики

Пример 21

Преобразовать структурную схему системы АРУ (рис. 21.1, a) в структурную схему следящей системы.

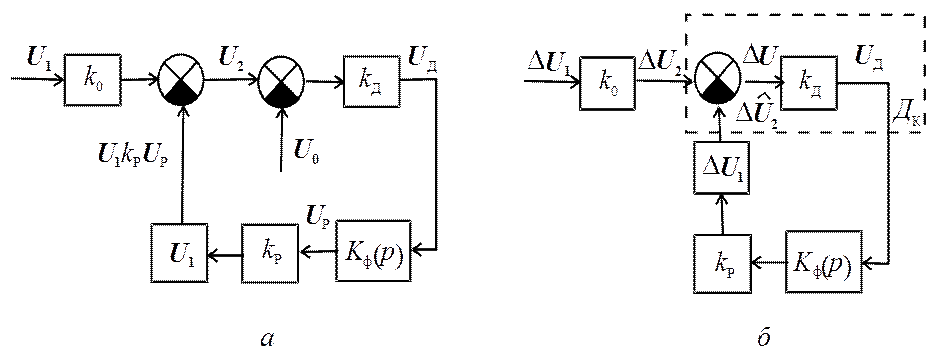Рис. 21.1

Решение

Рассматривая вместо переменных U₁ и U₂ их отклонения относительно пороговых уровней: DU₁=U₁–U₀/k₀ и DU₂=U₂–U₀, преобразуем структурную схему к виду (рис. 21.1, б). Эта система слежения за параметром DU₂, а выходной переменной является оценка D этого параметра. Дискриминатор (амплитудный) формирует напряжение пропорциональное рассогласованию DU=U₂–D.

Пример 22

Провести анализ устойчивости системы АРУ, полагая, что в качестве ФНЧ используется RС-фильтр с постоянной времени Т, а передаточные функции других элементов имеют вид

а)K_д(p)=k_д;

б)K_д(p)=k_д/(1+T_дp).

Решение

Анализ проведем на основе структурной схемы (рис. 1.15, б), используя частотный метод Найквиста (см. п. 4) и полагая  (что соответствует стационарной системе).

Передаточную функцию разомкнутой системы представим в виде:

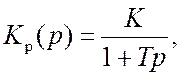                                           (22.1)

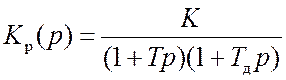                                (22.2)

для вариантов (а) и (б) соответственно (K=k_дk_рDU₁ – усиление разомкнутой системы).

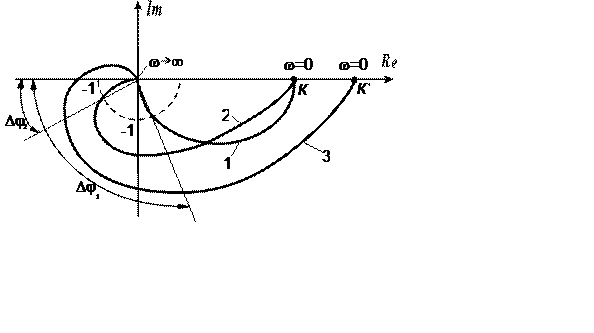
Рис. 22.1

АФХ разомкнутой системы, построенные с использованием (22.1) и (22.2), представлены на рис. 22.1 (соответственно, кривые 1 и 2). Как видно из рисунка, система устойчива в обоих случаях при любых значениях K. Однако во втором случае запас устойчивости по фазе может оказаться недостаточным, так как наличие в системе других (не учтенных при анализе) инерционных звеньев (например, регулируемого усилителя или УПТ) может привести к нарушению устойчивости при большом уровне сигнала (кривая 3).

Пример 23

Для системы АПЧ, структурная схема которой изображена на рис. 23.1, выбрать требуемое усиление K=k_дk_рk_г и постоянную времени Т из условия обеспечения заданных показателей качества: быстродействие t_п<0,01с; перерегулирование e<30%; точность – не хуже 1% (статическая ошибка).

   ;

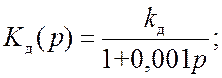
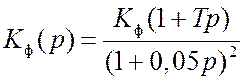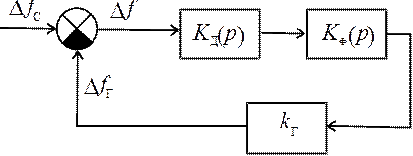
Рис. 23.1

Решение

Рассматриваемой статической системе соответствует типовая ЛАХ, представленная на рис. 23.2. Значения частот сопряжения:    (требуется определить). Наклон отдельных участков ЛАХ кратен –20дБ/дек (задан цифрами от 0 до 2).

Для обеспечения необходимого запаса устойчивости и качества переходного процесса участок ЛАХ с наклоном –20дБ/дек должен иметь протяженность не менее декады и располагаться симметрично относительно частоты среза w_ср.

Рис. 23.2

Значение частоты среза определим по заданному времени переходного процесса

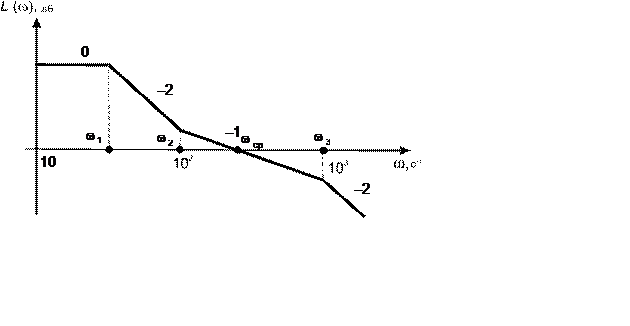
w_ср.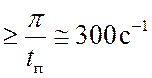

Выберем , а частоту сопряжения , что соответствует Т=0,01c. Определяем значение ФЧХ на частоте среза

j(w_cр)= –2arctg(w_ср/w₁)+arctg(w_ср/w₂) – arctg(w_cр/w₃)= –3p/4.

Запас устойчивости по фазе

j=p–|j(w_ср)|=p/4,

что является приемлемым. Запас по усилению не определяем, так как ФЧХ не пересекает горизонтальную линию –p (достигает ее лишь асимптотически при w®¥).

Устанавливаем связь между частотой w_cр и усилением K, используя ЛАХ разомкнутой системы

20lgK– 40lg(w₂/w₁)–20lg(w_cр/w₂)=0

или   .

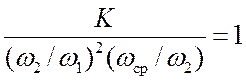Отсюда находим K=(w₂/w₁)²(w_cр/w₂)=100.

Для статистической ошибки запишем (см. п. 5)

,

что удовлетворяет требованию по точности (1%).

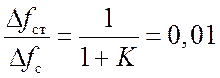Для определения перерегулирования рассчитаем резонансную частоту . Показатель колебательности М для АЧХ замкнутой системы определяется отношением w_cр/w₀: для w_cр/w₀=2 он составляет приблизительно 1,3 (см. лекцию 10). По виду универсальной переходной характеристики при М=1,3 находим перерегулирование e<30%, что соответствует требуемому значению.

Пример 24

Определить оптимальную шумовую полосу следящего фильтра, представленного структурной схемой на рис. 24.1, полагая, что воздействие F_д(t), возмущение df_г(t) и помеха n(t) – независимые стационарные случайные процессы cсоответственно с энергетическими спектрами

S_Д(w)=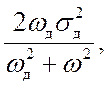       S_н(w)=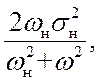

S_n(w)=N₀.

Решение

Представим частотную ошибку в виде

f=f_Д+f_н+f_n,

где составляющие f_д, f_н и f_n определяют соответственно ошибки, обусловленные флуктуациями доплеровской частоты, частотным шумом подстраиваемого генератора и помехой.

Дисперсия результирующей ошибки равна сумме дисперсий ее составляющих:

Дисперсия динамической ошибки, обусловленной искажениями воздействия вследствие конечной полосы пропускания замкнутой системы, равна

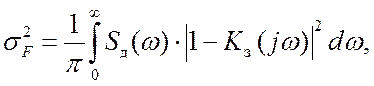                            (24.1)

где K_з(jw) – амплитудно-фазовая характеристика замкнутой системы.

На основе структурной схемы находим

                         (24.2)

где K=k_дk_иk_г – добротность системы по скорости.

Используя (24.1) и (24.2), получаем (см.п. 5)

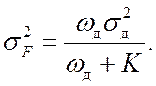                                                 (24.3)

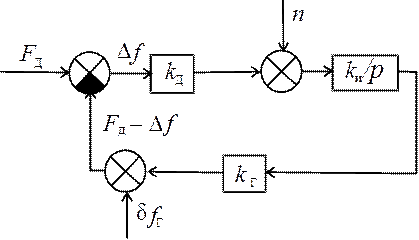
Рис. 24.1

Аналогично для дисперсии составляющей ошибки, обусловленной нестабильностью частоты ПГ, можем записать  

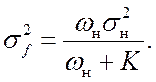                                      (24.4)

Здесь учтено, что передаточные функции для ошибки по возмущению df_г и по воздействию F_д отличаются лишь знаком (квадраты АЧХ в обоих случаях одинаковы |1 –K_з(jw)|²).

Дисперсия шумовой составляющей ошибки

                                           (24.5)

где 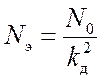 – спектральная плотность эквивалентного частотного шума;

F_щ= K/4 – шумовая полоса замкнутой системы.

Используя (24.3) – (24.5), для дисперсии результирующей ошибки запишем

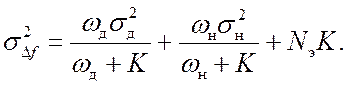                     (24.6)