Одним из главных возражений против модели КФО была высокая прозрачность аморфных халькогенидов в области ниже четко определенного края поглощения. В настоящее время из других наблюдений практически точно установлено, что область существования хвостов плотности состояний в халькогенидах довольно ограничена. Такая модель, возможно, более верна в случае аморфного кремния.
Модель Дэвиса—Мотта
Согласно Дэвису и Мотту, хвосты
локализованных состояний должны быть довольно узкими, распространяясь в запрещенную
зону на несколько десятых электронвольта. Кроме того, эти авторы высказали предположение
о существовании зоны компенсированных уровней вблизи середины запрещенной зоны,
обязанной своим происхождением дефектам в случайной сетке атомов, т. е.
свободным связям, вакансиям и т. д. Схематическая модель Дэвиса — Мотта
представлена на рис. 6, б, где через ECи ЕVобозначены энергии, разделяющие области локализованных и
делокализованных 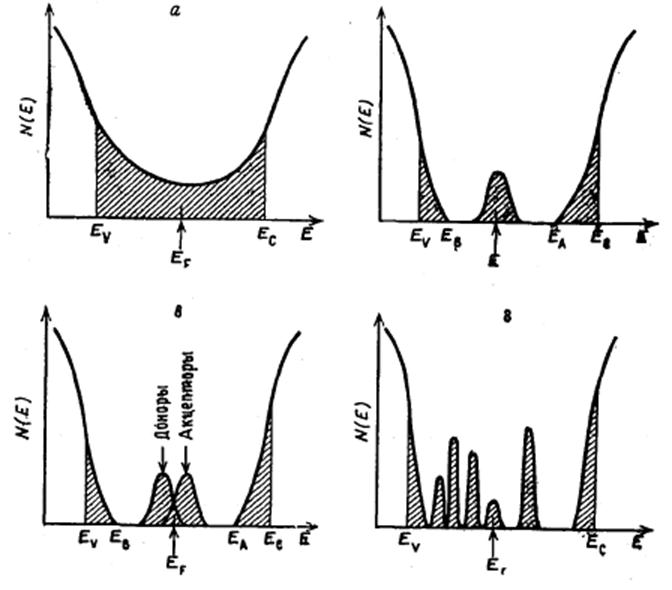
Рис. 6. Примерные кривые плотности состояний для аморфных полупроводников. а – модель Коэна–Фрицше–Овшинского; б – модель Дэвиса–Мота с зоной компенсированных уровней вблизи середины щели; в – модифицированная модель Дэвиса–Мота; г – «реальное» стекло с дефектными состояниями.
состояний. В центре этой зоны может произойти расщепление на донорную и акцепторные зоны, что приведет к закреплению уровня Ферми (рис. 6, в).
В этой модели постулируется существование порогов подвижности при энергиях, разделяющих локализованные состояния в хвостах от распространённых состояний.
Модель поляронов малого радиуса
Роль искажения решетки в присутствии «лишнего» носителя заряда в аморфном твердом теле детально анализировал Эмин. Он высказал предположение, что в некоторых аморфных полупроводниках носители заряда могут переходить в автолокализованное состояние (полярон малого радиуса), возникающее в результате поляризации окружающей решетки атомов. Обосновывая свою гипотезу, Эмин указывал на то, что наличие беспорядка в некристаллическом твердом теле приводит к замедлению движения носителей. Таким замедлением может вызываться локализация носителя, а тогда, если последний остается на данном атоме достаточно долго для того, чтобы могло произойти перераспределение атомов, он может индуцировать смещение атомов в своей непосредственной окрестности, что приведет к формированию полярона малого радиуса. Поскольку такой полярон по своей природе локален, отсутствие дальнего порядка в некристаллическом твердом теле, по-видимому, не будет оказывать существенного влияния на его движение.
Имеются два основных класса моделей: микрокристаллические модели и модели случайной структурной сетки. Микрокристаллические модели обладают серьезным недостатком: большое отношение числа поверхностных атомов к числу внутренних. Чтобы такая модель имела смысл, средний размер микрокристаллитов не должен превышать размеры нескольких элементарных ячеек, но в случае кристаллитов с размерами, равными трем элементарным ячейкам, около половины атомов приходится на границы микрокристаллитов. Таким образом, «соединительная ткань» этих границ столь же существенна, сколь и сами кристаллиты. В общем, это означает, что в пределе очень малого размера кристаллита микрокристаллическая модель становится неотличимой от модели случайной структурной сетки. Важнейшие аспекты локальной атомной структуры мы проиллюстрируем, рассматривая модель случайной структурной сетки Полка в применении к тетраэдрически связанным аморфным полупроводникам Si и Ge.
Модель Полка представляет собой структуру из «шариков» и «палочек», содержащую 440 атомов. Полк усовершенствовал свою модель, используя численные методы. В идеализированной структуре со случайной сеткой каждый атом связывается с ближайшими соседями, число которых отвечает его химической валентности. В одноэлементных системах все эти атомы одного типа, а в сплаве или соединении необходимо также указывать отдельные виды атомов, связанных с каждым отсчетным положением. Средние межатомные расстояния до ближайших соседей принимают равным значениям, которые они имеют в соответствующей кристаллической фазе, или (в более общем случае) равным сумме соответствующих ковалентных радиусов. Разброс длин связей задается малым, порядка ± 1% их среднего значения. В модели Полка для a-Si, a-Ge каждый атом имеет четыре ближайших соседа, расположенных в тетраэдрической геометрии. Допускаются отклонения углов связей, а поэтому тетраэдры обычно искажаются. В модели Полка углы связей распределяются около их среднего значения 109°28' со средним отклонением ±10° и максимальным отклонением ±20°. Случайный характер сетки возникает в результате статистического распределения двугранных углов. Все атомы в модели Полка входят в пятичленные или шестичленные кольца. Отношение тех и других в модели Полка равно 1:4, а в кристаллических фазах с алмазоподобной структурой Si и Ge все атомы находятся в шестичленных кольцах. Средним углом связи и его распределением определяются среднее расстояние и его распределение до второго соседа. При большей вариации двугранного угла практически исчезает какое-либо характеристическое расстояние до третьего соседа.
Применение моделей случайной сетки к одноэлементным системам, содержащим двух- или трехвалентные атомы, ставит интересные вопросы о топологии структурной сетки. Локальная топология случайной сетки четырехвалентных атомов трехмерна, трехвалентных — двумерна и двухвалентных — одномерна. Более низкая координация дает возможность реальному твердому телу отклоняться от полностью связанной сетки за счет введения отдельных структурных единиц. Получающееся твердое тело можно рассматривать как смесь молекулярных и полимерных структурных
единиц. Отдельные структурные единицы в a-Se были идентифицированы как кольцевые молекулы Se8, в a-As — как пирамидальные молекулы, а в стеклах As–S и Ge–S с избытком S — как кольцевые молекулы S8. Модели случайной сетки были также построены для соединений аморфных полупроводников [1].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.