Условия моделирования денежных потоков
1) С каждым проектом связывается определенный денежный поток. Деньги на выходе ( выходной капитал ), деньги на входе ( инвестиционный капитал ). Чистый денежный отток: превышение расходов над доходами. Чистый денежный приток: наоборот.
2) Все временные интервалы должны быть равными и соответствовать периоду финансового контроля.
3) В течение первого периода ставка финансирования не изменяется.
Коэффициент дисконтирования – коэффициент, отражающий убывание денежной массы
r ( к ) = 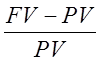 ,
где
,
где
FV - не дисконтированный денежный поток
PV - общая величина диск. дохода
Денежные потоки:
· однородные ( инвестиция совершается в начале, а выплаты происходят в течение всего периода )
 |
· неоднородные (в течение проекта можно делать инвестиции )
 |
Однородный денежный поток с равномерной величиной выплат – аннуитет.
Показатели экономической эффективности процесса
1) Чистый дисконтированный
доход NVP = ![]()
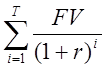 -
- 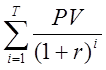 .
.
T – число периодов
Если необходимо добавить риск:
1 + р = ( 1 + r
) * ( 1+ i ) ![]() p = i + r + r * i –
мы пользуемся упрощенной формулой.
p = i + r + r * i –
мы пользуемся упрощенной формулой.
2) Индекс рентабельности инвестиций
PI
= 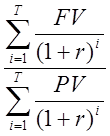 .
.
3) Внутренняя норма рентабельности инвестиций
r = IRR, при 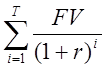 -
-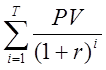 = 0
= 0
4) Модифицированная внутренняя норма рентабельности инвестиций ( для неоднородных денежных потоков )
r = MIRR при
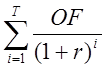 -
- 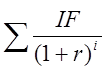 = 0,
= 0,
OF – отток,
IF – приток.
5) Срок окупаемости инвестиций
PP = min T ( минимальное время в минутах, в течение которого PV = FV ).
6) Дисконтированный срок окупаемости инвестиций
DPP - минимальный срок, при котором соблюдается равенство дисконтированных денежных потоков.
1) Коэффициент эффективности инвестиций
ARR = 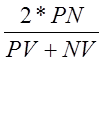 , PN
– чистая прибыль.
, PN
– чистая прибыль.
NV – остаточная стоимость результатов проекта.
Задача *:
Предприятие рассматривает возможность инвестирования средств в проект по разработке и изготовлению нового оборудования. Стоимость проекта - 10 млн руб. Срок эксплуатации 5 лет, износ начисляется по линейному методу. Расходы по утилизации линии и стоимость от продажи металлолома равны. Выручка от реализации продукции по годам прогнозируется в следующих объемах: 6800, 7400, 8200, 8000, 6000. Текущие расходы вычисляются так: 3400 в год с последующим ежегодным приростом на 3 %. Ставка налога на прибыль – 30%. Определить все коэффициенты, отражающие экономическую эффективность затрат.
|
1 |
2 |
3 |
4 |
5 |
|
|
1) Объем реализации в тыс. руб |
6800 |
7400 |
8200 |
8000 |
6000 |
|
2) текущие расходы |
3400 |
3502 |
3607 |
3715 |
3827 |
|
3) износ |
2000 |
2000 |
2000 |
2000 |
2000 |
|
4) налогооблагаемая прибыль: 1)-2)-3) |
1400 |
1898 |
2593 |
2285 |
173 |
|
5) чистая прибыль: 4)*0,07 |
980 |
1329 |
1815 |
1599 |
121 |
|
1) чистый денежный поток: 3) + 5) |
2980 |
3329 |
3815 |
3599 |
2121 |
![]() r = 0,19 NPV
r = 0,19 NPV
 e
e![]()
![]()
![]() f ( r
f ( r![]() ) IRR NPV=
-10000+
) IRR NPV=
-10000+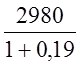 +
+ 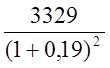 +
+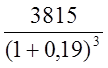 +
+
![]()
![]()
![]() f ( r
f ( r![]() )
r
)
r![]() r
r![]() r
r![]() r +
r + 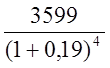 +
+ 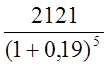 =
- 198
=
- 198
Таким образом, мы не закрываем
первоначальную денежную инвестицию. Это 2% ![]() можно
определить как нейтральное состояние.
можно
определить как нейтральное состояние.
Свойство аддитивности: Если есть
два проекта A и B![]() NPV (A
+ B ) = NPV ( A)
+ NPV ( B ).
NPV (A
+ B ) = NPV ( A)
+ NPV ( B ).
PI = -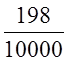 = -0,02.
= -0,02.
Расчет IRR
![]() FV =
FV = 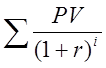 = такая норма
дисконтирования, при которой заданная инвестиция, будет возвращена с учетом
дисконтирования. = PV *
= такая норма
дисконтирования, при которой заданная инвестиция, будет возвращена с учетом
дисконтирования. = PV * 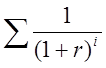 = PV
*
= PV
* 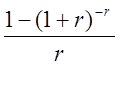
( Если PV = const )
Из графика ( принцип подобия ):
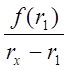 =
= 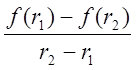 ,
f (r
,
f (r![]() )*( r
)*( r![]() -
r
-
r![]() ) = ( r
) = ( r![]() -
r
-
r![]() ) * ( f (r
) * ( f (r![]() ) – f ( r
) – f ( r![]() ) ),
) ),
r![]() = r
= r![]() +
+ 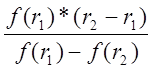
![]() 0,18
0,18
PI = -0,02
![]() NPV = -198 f
( r
NPV = -198 f
( r![]() ) = -198 при
r
) = -198 при
r![]() = 0,19.
= 0,19.
![]() Примем r
Примем r![]()
![]() 0,17,
тогда f (r
0,17,
тогда f (r![]() )
= 253; отсюда r
)
= 253; отсюда r![]() =
0,18 IRR = 0,18.
=
0,18 IRR = 0,18.
r может
меняться на 15 – 20 %. В этом проекте нет нормы риска ![]() проще
вложить в банк.
проще
вложить в банк.
Мягкие условия принятия проекта IRR![]() - IRR
- IRR ![]() > 0 ( в данном случае 0
)
> 0 ( в данном случае 0
)
IRR![]() = δ * IRR
= δ * IRR ![]() (δ>1 – задаваемая норма платы за риск );
(δ>1 – задаваемая норма платы за риск );
γ = 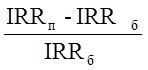 , γ –
плата за риск.
, γ –
плата за риск.
Расчет ARP
ARP = 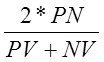 =
=
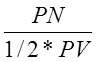 =
= 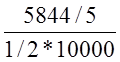 =
0,23, при NV = 0.
=
0,23, при NV = 0.
Модифицированная внутренняя норма рентабельности
![]()
![]() 11 8
12Для расчета MIRRиспользуем метод
11 8
12Для расчета MIRRиспользуем метод
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 7 кумулятивных сумм
7 кумулятивных сумм
![]()
![]()
![]() -10
-15
-10
-15
![]() -13,4
-13,4![]() 44,58
44,58
-23,4
Все, что с “-“ – дисконтируется, что с “ + “ – кумулируется.
![]() = 0,12
= 0,12
NPV = -10 - ![]() +
+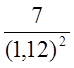 +
+
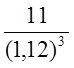 +
+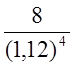 +
+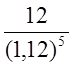 = 1,9.
= 1,9.
r![]() = 0,18
= 0,18
f(r![]() ) = -10 -
) = -10 -![]() + …+
+ …+ 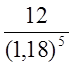 =
- 1,62.
=
- 1,62.
IRR = 15 %; (γ = 25 % - хорошо ).
( 1 + MIRR )![]() =
=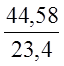 = 1,91.
= 1,91. ![]() MIRR = 0,138.
MIRR = 0,138.
γ = 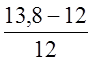 =
15 %.
=
15 %.
![]() Задача.
Задача.
![]()
![]()
![]()
![]() 150 80 15 15 10
150 80 15 15 10
![]()
![]() А
А
![]() -200
-200
![]() 50
50 90 110
50
50 90 110
![]()
![]()
![]() 20
20
В
![]()
![]() -200
-200
|
NVP у.е. |
IRR |
||||
|
r = 5 % |
10 % |
15 % |
20 % |
% |
|
|
А |
48,6 |
30,2 |
14,3 |
0,5 |
20,2 |
|
B |
76,5 |
34,3 |
0,7 |
-26,6 |
15,1 |
При r = 20 %: А и В отвергаются.
При r = 15 %: А – принимается, В – отвергается.
При r = 10 %: А – скорее да, В – скорее нет.
При r = 5 %: А – отвергается, В – принимается ( необходим другой инструмент ).
|
0 |
1 |
2 |
3 |
4 |
5 |
|
200 200 |
220 |
242 |
266,62 |
292 |
322,б1 |
|
-200 |
150 |
245 |
Диск. доход
Недиск.
доход
Шаг 1:
прикидываем, где близка недиск. Сумма = диск![]() 2,2
–окончание
2,2
–окончание
А: 80 + 150*1,1 = 245
В: 110 + 90*1,1
+ 50*1,1![]() + 50*1,1
+ 50*1,1![]() +
20*1,1
+
20*1,1![]() = 365,33
= 365,33
![]()
![]() А:
Tд = 1 г 11,5 мес 165
А:
Tд = 1 г 11,5 мес 165
![]()
![]()
![]() 80
80
![]() 12 мес
12 мес
![]() T:
150
T:
150
![]()
![]() 80 70/12 = 5,6 мес
80 70/12 = 5,6 мес
![]() 0
150-200 = 50
0
150-200 = 50
12
50/5,6 ![]() 1 г 8,6 мес
1 г 8,6 мес
В: Т![]() 4г ( 20+50+50+90 = 210 )
4г ( 20+50+50+90 = 210 )
Тд![]() 5 л.
5 л.
Динамика проектов

![]() NPV
NPV
А
 |
![]()
![]() NPV В Точка Фишера (
безразличия ) – норма дисконтирования,
NPV В Точка Фишера (
безразличия ) – норма дисконтирования,
при которой чистые дисконтированные доходы ( NPV ) для 2
![]() r или более проектов имеют одинаковые
значения.
r или более проектов имеют одинаковые
значения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.