


























ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ
Часть 2.
Электромеханические переходные процессы
Список рекомендуемой литературы:
1. Веников В.А. Переходные электромеханические процессы в электрических системах. М.: ВШ, 1985.
2. Жданов П.С. Вопросы устойчивости электрических систем. Под ред. Л.А. Жукова. М.: 1979.
3. Жданов П.С. Устойчивость электрических систем. Учебник для вузов.
4. Анисимова и др. Переходные процессы в электрических системах в примерах и иллюстрациях.
5. Разумов. Устойчивость электрических систем.
2.3.2. Явнополюсный генератор (гидрогенератор)
Для вывода угловой характеристики мощности рассмотрим случай последовательной цепи без активных сопротивлений и поперечных проводимостей. Схема замещения простейшей системы в этом случае будет иметь вид рис.2.29, а соответствующая ей векторная диаграмма токов и напряжений рис.2.30.
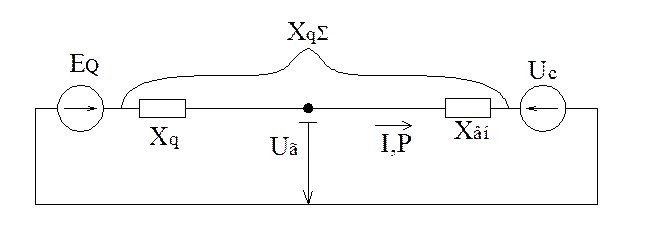
Рис.2.29. Схема замещения простейшей системы с явнополюсным генератором.
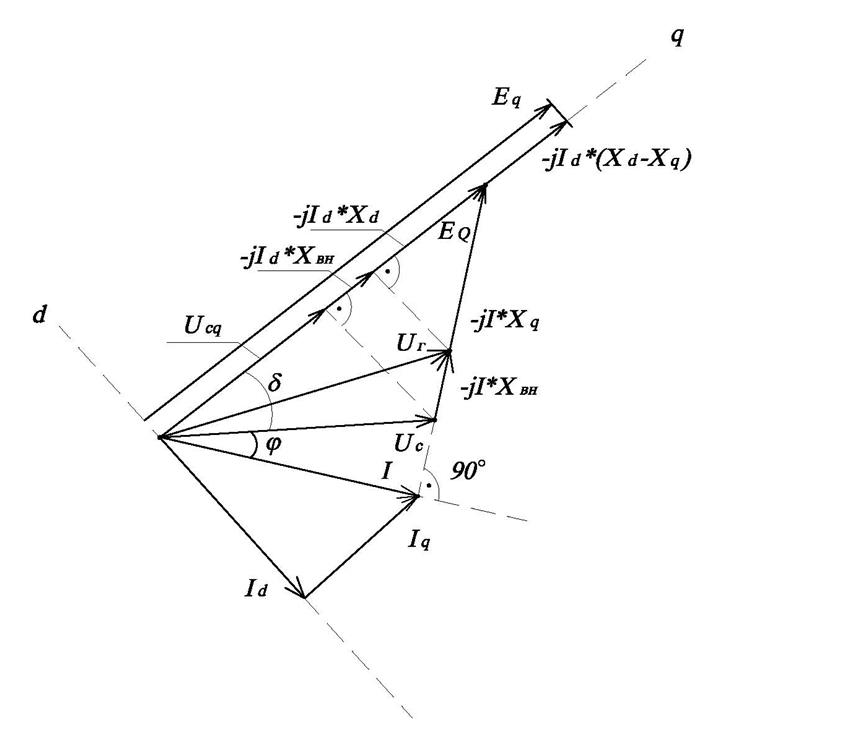
Рис.2.30. Векторная диаграмма токов и напряжений простейшей системы рис.2.29.
![]() , (2.47)
, (2.47)
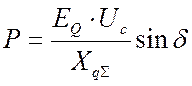 , (2.48)
, (2.48)
![]() , (2.49)
, (2.49)
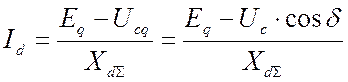 . (2.50)
. (2.50)
Подставив (2.50) в (2.49), получаем:
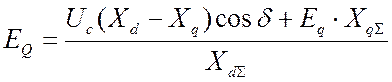 , (2.51)
, (2.51)
подставляя (2.51) в (2.48) окончательно получаем выражение угловой характеристики:
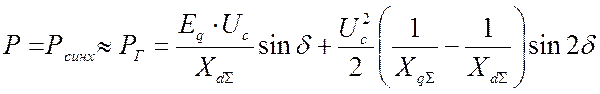 . (2.52)
. (2.52)
Таким образом, оказывается, что при отсутствии
возбуждения (![]() ) явнополюсный генератор способен
вырабатывать синхронную активную мощность, определяемую вторым членом в (2.52).
) явнополюсный генератор способен
вырабатывать синхронную активную мощность, определяемую вторым членом в (2.52).
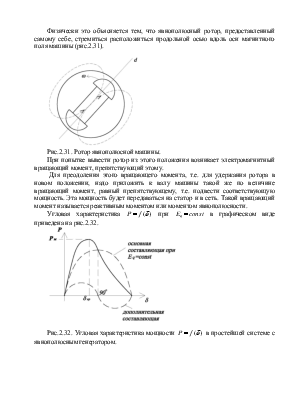
Физически это объясняется тем, что явнополюсный ротор, предоставленный самому себе, стремиться расположиться продольной осью вдоль оси магнитного поля машины (рис.2.31).
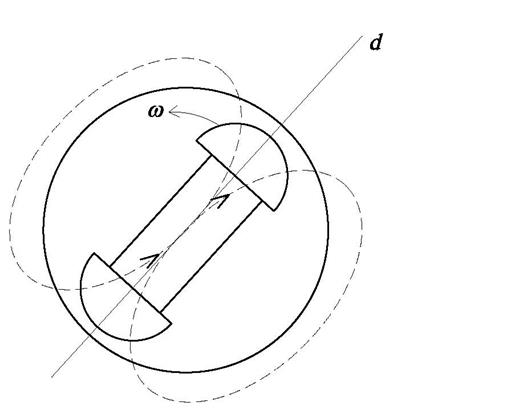
Рис.2.31. Ротор явнополюсной машины.
При попытке вывести ротор из этого положения возникает электромагнитный вращающий момент, препятствующий этому.
Для преодоления этого вращающего момента, т.е. для удержания ротора в новом положении, надо приложить к валу машины такой же по величине вращающий момент, равный препятствующему, т.е. подвести соответствующую мощность. Эта мощность будет передаваться на статор и в сеть. Такой вращающий момент называется реактивным моментом или моментом явнополюсности.
Угловая характеристика ![]() при
при
![]() в графическом виде приведена на рис.2.32.
в графическом виде приведена на рис.2.32.
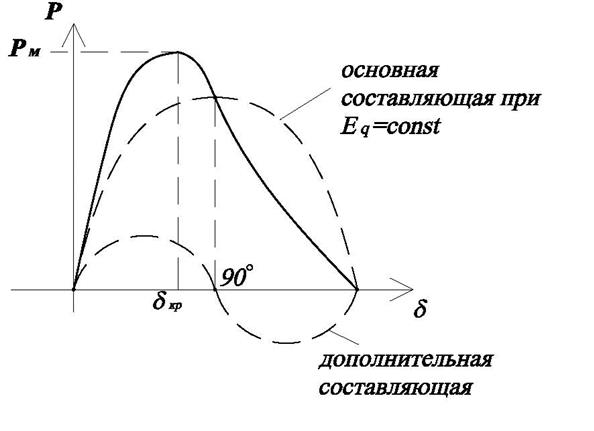
Рис.2.32. Угловая характеристика мощности ![]() в простейшей системе с явнополюсным
генератором.
в простейшей системе с явнополюсным
генератором.
![]() и
и ![]() можно найти известным из математики
способом – взятием производной
можно найти известным из математики
способом – взятием производной ![]() и приравниванием
ее нулю:
и приравниванием
ее нулю:
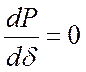 . (2.53)
. (2.53)
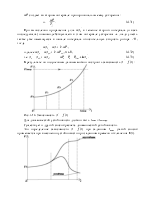
Из этого уравнения находится ![]() и,
подставив найденное значение
и,
подставив найденное значение ![]() в выражение для P
(2.52), найдем предел мощности
в выражение для P
(2.52), найдем предел мощности ![]() , соответствующий
этому углу
, соответствующий
этому углу ![]() (см. рис.2.32). Делать это следует,
написав выражение (2.52) для P в численном виде. Обычно амплитуда дополнительной
составляющей мощности не превышает
(см. рис.2.32). Делать это следует,
написав выражение (2.52) для P в численном виде. Обычно амплитуда дополнительной
составляющей мощности не превышает ![]() от амплитуды
основной составляющей, и поэтому влияние ее на величину
от амплитуды
основной составляющей, и поэтому влияние ее на величину![]() не
велико. Поэтому в практических расчетах устойчивости явнополюсную машину
заменяют неявнополюсной с синхронным индуктивным сопротивлением равным
не
велико. Поэтому в практических расчетах устойчивости явнополюсную машину
заменяют неявнополюсной с синхронным индуктивным сопротивлением равным ![]() явнополюсной машины.
явнополюсной машины.
3. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ ПРОСТЕЙШЕЙ СИСТЕМЫ
3.1. Условия статической устойчивости простейшей системы при отсутствии АРВ у генератора
При отсутствии активных сопротивлений, и, если пренебречь потерями в стали и меди обмоток статора генератора, имеем:
![]() .
.
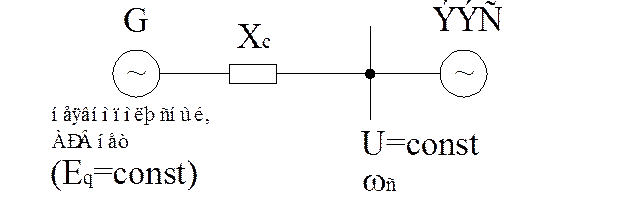
Рис.3.1. Простейшая система с неявнополюсным генератором, АРВ нет.
Уравнение движения ротора генератора:
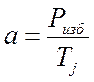 , (3.1)
, (3.1)
где ![]() ,
,
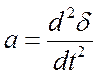 - угловое
ускорение (ранее обозначаемое α).
- угловое
ускорение (ранее обозначаемое α).
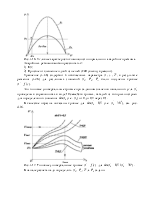
Установившемуся режиму должна соответствовать должна
соответствовать точка пересечения зависимостей ![]() и
и
![]() (см. рис.3.1).
(см. рис.3.1).
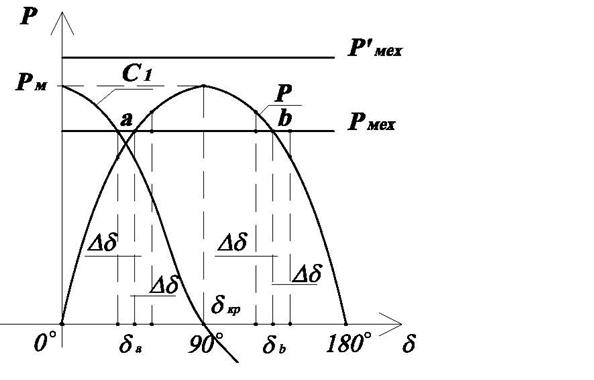
Рис.3.2. Угловая характеристика мощности и механическая характеристика генератора.
Можно сделать замечание, что установившийся режим
возможен лишь в тех случаях, когда ![]() . Если же имеем
. Если же имеем ![]() (см.
(см. ![]() на
рис.3.1), то
на
рис.3.1), то ![]() , ускорение
, ускорение ![]() ,
т.е. скорость вращения ротора непрерывно увеличивается, и генератор не может
работать синхронно с системой ЭЭС.
,
т.е. скорость вращения ротора непрерывно увеличивается, и генератор не может
работать синхронно с системой ЭЭС.
Поэтому ![]() называется
пределом мощности электропередачи:
называется
пределом мощности электропередачи:
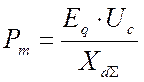 , где
, где ![]() .
.
Если ![]() , то, как видно
из рис.3.1, баланс мощностей возможен в двух точках (а и b).
Предположим, что в исходном установившемся режиме скорость вращения ротора
генератора равна синхронной
, то, как видно
из рис.3.1, баланс мощностей возможен в двух точках (а и b).
Предположим, что в исходном установившемся режиме скорость вращения ротора
генератора равна синхронной ![]() , в таком случае
, в таком случае ![]() не изменяется и баланс мощностей
сохраняется сколь угодно долго (см. рис.3.1 и 3.2).
не изменяется и баланс мощностей
сохраняется сколь угодно долго (см. рис.3.1 и 3.2).
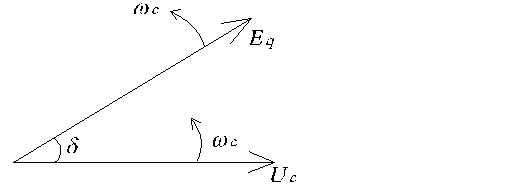
Рис.3.3. Векторная диаграмма установившегося режима простейшей системы.
Однако для того чтобы установившийся режим мог длительно существовать, недостаточно соблюдения условия:
![]() . (3.2)
. (3.2)
Режим должен быть еще устойчив по отношению к малым возмущениям, которые происходят непрерывно. Режим, устойчивый при малых возмущениях, называется статически устойчивым режимом. Чтобы проверить статическую устойчивость режима, необходимо исследовать переходный процесс, возникающий при сколь угодно малом возмущении режима. Если после такого переходного процесса система вернется к исходному состоянию, то она статически устойчива, если – нет, то неустойчива.
Рассмотрим режим в точке ![]() на
рис.3.1.
на
рис.3.1.
Предположим, что в результате какого-нибудь
кратковременного возмущающего воздействия ![]() изменился
на сколь угодно малую величину
изменился
на сколь угодно малую величину ![]() , равную:
, равную:
![]() .
.
Если ![]() , то получим
, то получим ![]() , т.е.
, т.е. ![]() и
скорость
и
скорость ![]() становиться меньше синхронной
скорости
становиться меньше синхронной
скорости ![]() (
(![]() ).
В результате
).
В результате ![]() уменьшается, т.е. возвращается к
своему исходному значению
уменьшается, т.е. возвращается к
своему исходному значению ![]() .
.
Если ![]() , то получим
, то получим ![]() , т.е.
, т.е. ![]() и
скорость
и
скорость ![]() становиться больше синхронной
скорости
становиться больше синхронной
скорости ![]() (
(![]() ).
В результате
).
В результате ![]() увеличивается, т.е. возвращается к
своему исходному значению
увеличивается, т.е. возвращается к
своему исходному значению ![]() .
.
При отклонении угла от значения ![]() возникает избыточный вращающий
момент, стремящийся вернуть генератор в исходное состояние, но, вернется ли он
в это состояние, зависит от знака коэффициента демпфирования
возникает избыточный вращающий
момент, стремящийся вернуть генератор в исходное состояние, но, вернется ли он
в это состояние, зависит от знака коэффициента демпфирования ![]() . Если
. Если ![]() ,
то отклонение угла под воздействием асинхронного вращающего момента
ликвидируется, и восстанавливается исходный режим. В этом случае система
статически устойчива, характер переходного процесса зависит от величины
,
то отклонение угла под воздействием асинхронного вращающего момента
ликвидируется, и восстанавливается исходный режим. В этом случае система
статически устойчива, характер переходного процесса зависит от величины ![]() (см. рис.3.3).
(см. рис.3.3).
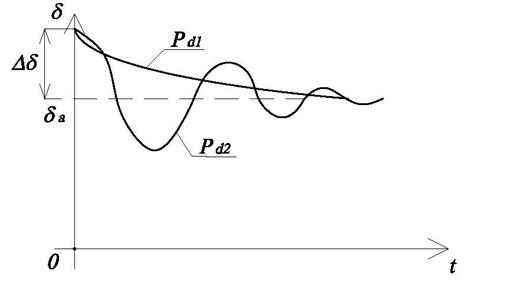
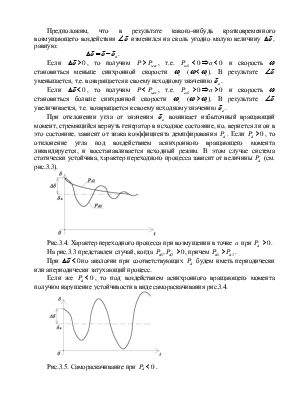
Рис.3.4. Характер переходного процесса при возмущении
в точке ![]() при
при ![]() .
.
На рис.3.3 представлен случай, когда ![]() , причем
, причем ![]() .
.
При ![]() по аналогии при
соответствующих
по аналогии при
соответствующих ![]() будем иметь периодически
или апериодически затухающий процесс.
будем иметь периодически
или апериодически затухающий процесс.
Если же ![]() , то под
воздействием асинхронного вращающего момента получим нарушение устойчивости в
виде самораскачивания рис.3.4.
, то под
воздействием асинхронного вращающего момента получим нарушение устойчивости в
виде самораскачивания рис.3.4.
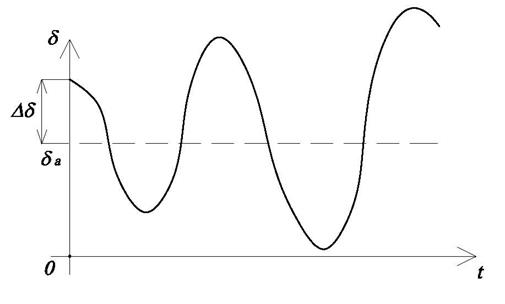
Рис.3.5. Самораскачивание при ![]() .
.
При ![]() - аналогично.
- аналогично.
В любом случае при ![]() ,
генератор, в результате самораскачивания, выпадает из синхронизма в сторону
увеличения скорости.
,
генератор, в результате самораскачивания, выпадает из синхронизма в сторону
увеличения скорости.
Теперь рассмотрим режим, соответствующий точке ![]() на рис.3.1.
на рис.3.1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.