Переходные процессы в электроэнергетических системах. Часть 2 (Электромеханические переходные процессы), страница 2

Если отклонение угла , то получим , т.е.  и скорость  становиться больше синхронной скорости  (). В результате  увеличивается. С ростом  мощность продолжает падать, что вызывает дальнейшее еще более интенсивное увеличение , в результате генератор выпадает из синхронизма в сторону увеличения скорости вращения.

Если отклонение угла , то получим , т.е.  и скорость  становиться меньше синхронной скорости  (). В результате  уменьшается. При  после затухающего колебательного переходного процесса устанавливается режим соответствующий точке . А при  получим самораскачивание с последующим выпадением из синхронизма (см. рис.3.5).

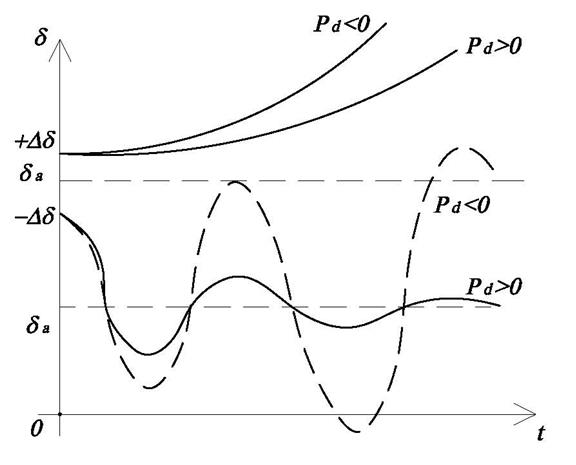
Рис.3.6. Характер переходного процесса при возмущениях в точке  при  и .

Математические возрастающая часть характеристики мощности  от убывающей ее части отличается тем, что на возрастающей части:

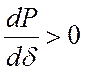, а на убывающей .

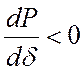Следовательно, критерием статической устойчивости (математическим признаком) рассматриваемой системы (простейшей электропередачи) при отсутствии на генераторе АРВ является условие:

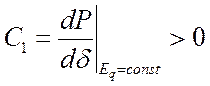,         .                                                 (3.3)

Величина  называется синхронизирующей мощностью. В данном случае при угловой характеристике, описываемой формулой:

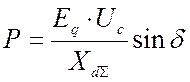 имеем 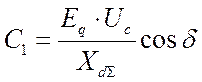.                               (3.4)

(см. рис.3.1., где С₁ – синхронизирующая мощность).

 может служить характеристикой степени устойчивости режима. Это видно из следующего.

, если находимся в точке  и проведем касательную к кривой .

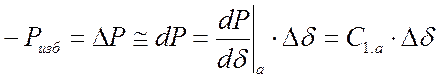,          ,       (3.5)

т.е.  при некотором заданном отклонении угла  ().

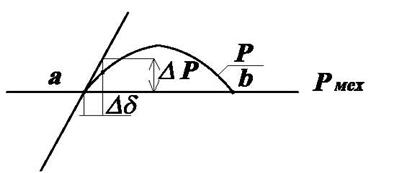
Рис.3.7. К определению .

 пропорциональна  при некотором заданном отклонении .

Если рассматривать возрастающую часть характеристики, то величина  характеризует собой силу, стремящуюся вернуть ротор генератора в исходное положение, если он от него отклоняется. И эта величина при заданном  пропорциональна синхронизирующей мощности. Только благодаря этим силам и возможна синхронная работа генераторов в электрической системе. Отсюда и происходит название «синхронизирующая мощность».

Величина  зависит от  в исходном режиме, т.е. от активной нагрузки генератора. Чем больше , тем больше  и тем меньше , т.е. тем менее устойчив режим работы генератора.

Рассматривалась простейшая электрическая передача без активных сопротивлений, но эти рассуждения будут справедливы  при любом характере связи генератора с приемной системой, т.к. в любом случае угловая характеристика мощности имеет две ветви (возрастающую и убывающую).

Из рис.3.1 и 3.5 видно, что режим электропередачи при  всегда устойчив, если  ( - исходный режим). Значит, для проверки статической устойчивости электропередачи достаточно определить предел мощности  и сравнить его с , которую предполагается передавать в приемную ЭЭС.

Таким образом, критерий  можно заменить критерием , практически это удобнее, чем пользоваться синхронизирующей мощностью. Но на практике желательно знать еще и степень устойчивости режима (запас устойчивости).

Работать близко к пределу мощности нельзя, необходим запас. Во-первых, из-за неизбежной неточности расчетов и исходных данных. Кроме того, запас устойчивости необходим и для непредвиденных изменений режима приемной ЭЭС, приводящих к ухудшению устойчивости (% снижения напряжения на шинах ЭЭС).

О степени устойчивости режима можно судить по величине коэффициента запаса статической устойчивости:

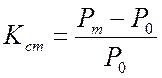.                                                                            (3.6)

Чем выше , тем устойчивее режим. Есть нормативы этого коэффициента. Нельзя допускать слишком низкого запаса устойчивости (). По нормативам  должен быть не менее 0,2 (20%) в нормальном режиме и не менее 0,08 (8%) в кратковременном послеаварийном режиме до вмешательства обслуживающего персонала в регулирование режима.

Таким образом, практический расчет статической устойчивости простейшей электропередачи сводится к определению предела мощности  и затем коэффициента . Кроме того, необходимо вычислить  и проверить условие  (если нет АРВ).

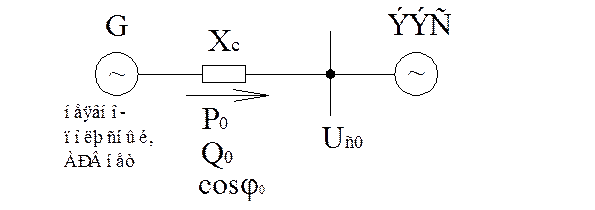
Рис.3.8.К определению максисмума электропередачи.

Для определения  необходимо знать , , , эти параметры обычно заданы, затем определить :

,                                          (3.7)

при отсутствии АРВ  и тогда :

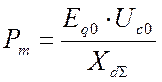.                                                                            (3.8)

Это справедливо для простейшего случая: неявнополюсный генератор, нет АРВ, нет активных сопротивлений, электропередача последовательная.

1.  ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ (ДУ) ПРОСТЕЙШЕЙ СИСТЕМЫ

Динамическая устойчивость – устойчивость по отношению к большим возмущениям. Устойчивость системы к малым возмущениям (статическая устойчивость) еще вовсе не означает устойчивость ее к большим возмущениям режима (динамическая устойчивость).

Самыми опасными возмущениями с точки зрения устойчивости являются КЗ, поэтому динамическую устойчивость рассматривают при КЗ.

Рассмотрим простейшую систему вида:

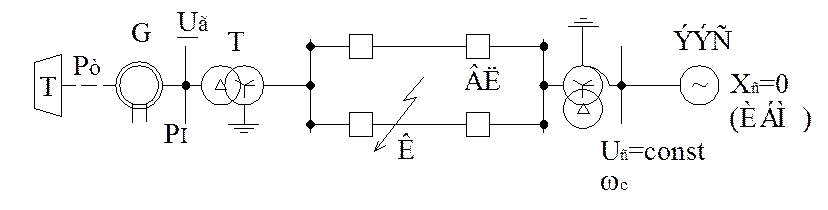
Рис.4.1. Простейшая система (электропередача).

Время существования КЗ мало (0,06-0,3с) до отключения его выключателем с обеих сторон. Рассмотрим электромеханический переходный процесс при этом условии:

Если нет АРВ:

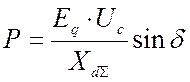,                                                                        (4.1)

если АРВ пропорционального действия:

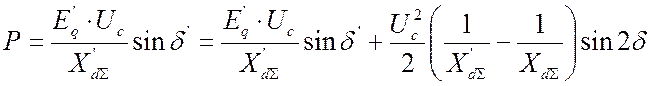,         (4.2)

если АРВ сильного действия:

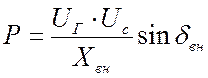.                                                                      (4.3)

При КЗ, учитывая, что переходная ЭДС  () измениться скачком не может, и постоянная времени затухания свободных составляющих токов , а нас интересует интервал времени , в этих условиях можно считать, что  для машин без демпферных контуров.

Но электромагнитные процессы в демпферных контурах очень быстры, и ими можно пренебречь. Значит, из всех формул (4.1), (4.2) и (4.3) можно взять (4.2), для простоты считая .