Если в исходном режиме работаем в точке ![]() (
(![]() )
система устойчива, даже если не отключать КЗ, и тем более устойчива, если его
отключить, т.к. сразу значительно возрастает площадка
)
система устойчива, даже если не отключать КЗ, и тем более устойчива, если его
отключить, т.к. сразу значительно возрастает площадка ![]() .
Т.е. в этом случае система, безусловно, устойчива, и дальнейшего анализа также
не требуется.
.
Т.е. в этом случае система, безусловно, устойчива, и дальнейшего анализа также
не требуется.
Таким образом, дальнейшие расчеты динамической
устойчивости необходимы только, если передаваемая мощность ![]() будет находиться в пределах:
будет находиться в пределах:
![]() . (4.15)
. (4.15)
В этом случае расчет по определению предельного
времени отключения КЗ ![]() начинается с определения
предельного угла отключения
начинается с определения
предельного угла отключения ![]() .
.
Поясняющий рисунок, необходимый для понимания записи
уравнения ![]() в развернутом виде с целью
определения
в развернутом виде с целью
определения ![]() приведен на рис.4.9.
приведен на рис.4.9.
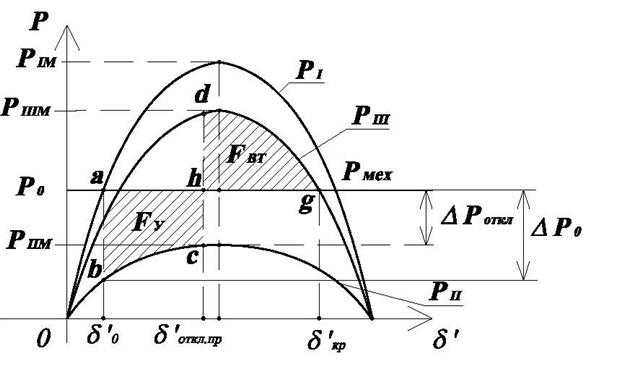
Рис.4.10. К определению ![]() .
.
С помощью рис.4.9, пользуясь правилом площадей можно
графически найти предельное значение угла, при котором нужно произвести
отключение поврежденной линии (![]() ) для того чтобы
добиться устойчивой работы.
) для того чтобы
добиться устойчивой работы.
Значение этого угла определяется равенством:
![]() .
.
Угол ![]() может быть найден
и аналитически, для большей наглядности, опираясь на рис.4.9.
может быть найден
и аналитически, для большей наглядности, опираясь на рис.4.9.
Действительно, приравнивая площади ![]() и
и ![]() (т.е.
(т.е.
![]() и
и ![]() )
получаем:
)
получаем:
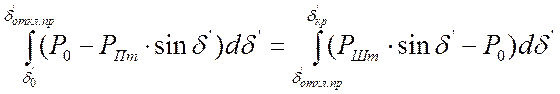 . (4.16)
. (4.16)
Отсюда после интегрирования можно выразить ![]() :
:
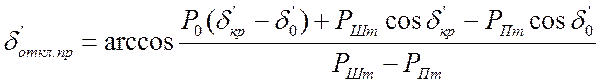 . (4.17)
. (4.17)
Подставляя в (4.17) значения:
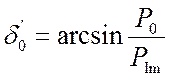 и
и 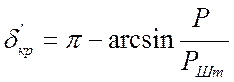 , (4.18)
, (4.18)
можно определить численное значение ![]() .
.
Однако для практических расчетов этого недостаточно.
Для того чтобы предъявить к выключателям те или иные требования в отношении
скорости отключения, необходимо знать не угол ![]() ,
а тот промежуток времени, в течение которого ротор успевает достигнуть этого
угла, т.е.
,
а тот промежуток времени, в течение которого ротор успевает достигнуть этого
угла, т.е. ![]() КЗ. Нам нужна зависимость
КЗ. Нам нужна зависимость ![]() в режиме короткого замыкания, чтобы
найти
в режиме короткого замыкания, чтобы
найти ![]() , но с помощью правила площадей
определить это время невозможно и приходится прибегать к другим методам анализа
динамической устойчивости.
, но с помощью правила площадей
определить это время невозможно и приходится прибегать к другим методам анализа
динамической устойчивости.
Искомой характеристикой ![]() является
решение уравнения движения ротора генератора в аварийном режиме, имеющего вид:
является
решение уравнения движения ротора генератора в аварийном режиме, имеющего вид:
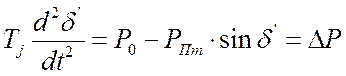 . (4.19)
. (4.19)
Решить это уравнение в общем виде невозможно,
поскольку оно нелинейно. Задачу приходится решать методами численного
интегрирования уравнений. Одним из таких методов является метод
последовательных интервалов, с помощью которого задача решается в конечных
приращениях. Но в начале рассмотрим частный случай записи (4.19), когда прямое
аналитическое решение уравнения движения возможно. Это случай трехфазного КЗ в
начале линии, т.е. когда ![]() . Действительно, при этом из (4.19) имеем:
. Действительно, при этом из (4.19) имеем:
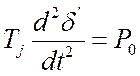 (4.20)
(4.20)
при начальных условиях:
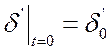 ;
; 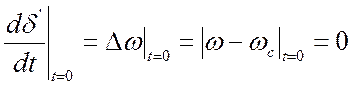 .
.
Решение уравнения (4.20) имеет вид:
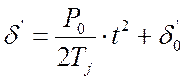 , (4.21)
, (4.21)
или в графической форме решение (4.21) имеет вид рис.4.10.
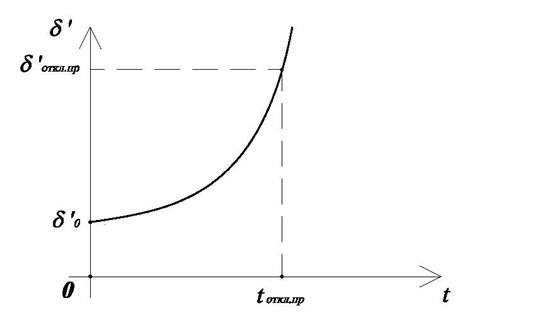
Рис.4.11. Зависимость ![]() при
при
![]() .
.
Подставляя в (4.21) в качестве ![]() ,
а в качестве
,
а в качестве ![]() получим:
получим:
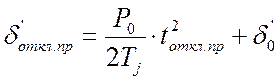 , (4.22)
, (4.22)
и, наконец, из (4.22) имеем:
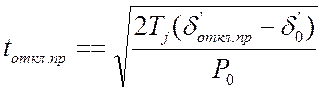 . (4.23)
. (4.23)
А если ![]() (т.е. например
авария в виде
(т.е. например
авария в виде ![]() ,
, ![]() ,
,
![]() ), то возможны:
), то возможны:
1) приближенный способ.
![]() ,. (4.24)
,. (4.24)
Грубо ![]() можно заменить
фиксированным значением:
можно заменить
фиксированным значением:
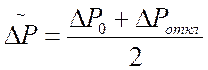 , (4.25)
, (4.25)
где ![]() , а
, а ![]() . (4.26)
. (4.26)
Тогда выражение для ![]() (4.25)
нужно подставить в (4.23) вместо
(4.25)
нужно подставить в (4.23) вместо ![]() .
.
2) численное интегрирование уравнения движения (4.21), т.е. метод последовательных интервалов (или метод шаг за шагом).
Весь переходный процесс качания машины разбивается на
ряд небольших интервалов времени ![]() , и для каждого из
этих интервалов последовательно вычисляется значение приращения
, и для каждого из
этих интервалов последовательно вычисляется значение приращения ![]() .
.
В момент КЗ отдаваемая генераторами мощность падает и
возникает избыток мощности ![]() . Для достаточно
малого интервала времени
. Для достаточно
малого интервала времени ![]() можно допустить,
что
можно допустить,
что ![]() в течение этого интервала
в течение этого интервала ![]() остается неизменным.
остается неизменным. ![]() принимаются обычно одинаковыми на
всем протяжении переходного процесса и в диапазоне от 0,02 с до 0,1 с.
Графическая интерпретация метода показана на рис.4.11.
принимаются обычно одинаковыми на
всем протяжении переходного процесса и в диапазоне от 0,02 с до 0,1 с.
Графическая интерпретация метода показана на рис.4.11.
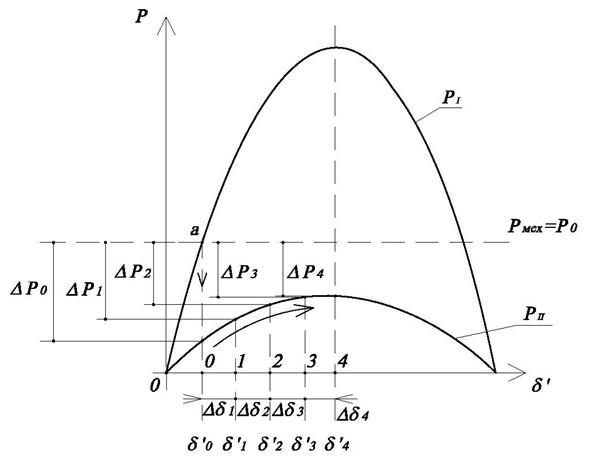
Рис.4.12. Графическая интерпретация метода последовательных интервалов.
По формулам равномерно ускоренного движения вычисляется приращение угла в течение первого интервала:
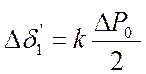 , (4.27)
, (4.27)
где 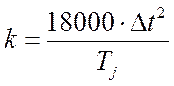 . (4.28)
. (4.28)
Зная приращение угла в первом интервале, можно найти абсолютное значение угла в конце этого интервала времени, или, что то же самое, в начале второго интервала:
![]() . (4.29)
. (4.29)
Для нового значения угла ![]() можно
определить избыток мощности
можно
определить избыток мощности ![]() :
:
![]() . (4.30)
. (4.30)
![]() создает во втором
интервале пропорциональные ему ускорения:
создает во втором
интервале пропорциональные ему ускорения:
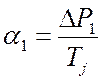 . (4.31)
. (4.31)
При вычислении приращения угла ![]() в
течение второго интервала (и всех последующих) помимо действующего в этом
интервале ускорения
в
течение второго интервала (и всех последующих) помимо действующего в этом
интервале ускорения ![]() , надо учесть также уже
имеющуюся в начале интервала относительную скорость ротора
, надо учесть также уже
имеющуюся в начале интервала относительную скорость ротора ![]() , тогда
, тогда
![]() ,
,
и далее ![]() , (4.32)
, (4.32)
т.е. ![]() ,
, ![]() . (4.33)
. (4.33)
В результате по полученным данным можно построить
зависимость ![]() :
:
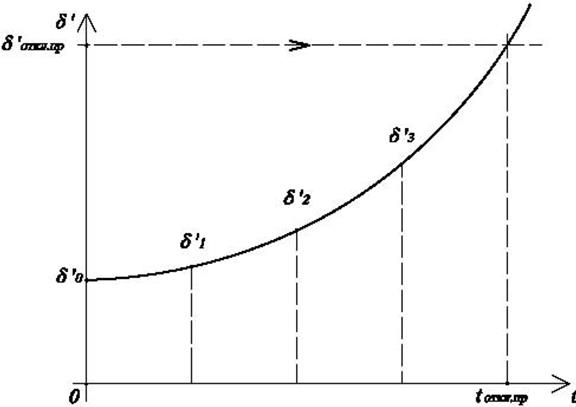
Рис.4.13. Зависимость ![]()
Для динамической устойчивости должно быть ![]() .
.
Существует и другой способ расчета динамической устойчивости.
Это определение зависимости ![]() при
заданном
при
заданном ![]() (такой способ применяется при
выяснении устойчивости при заданном времени отключения КЗ).
(такой способ применяется при
выяснении устойчивости при заданном времени отключения КЗ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.