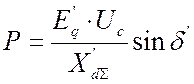Переходные процессы в электроэнергетических системах. Часть 2 (Электромеханические переходные процессы), страница 3

.                                                                        (4.4)

Т.е. генераторы могут замещаться  и , приложенной за .

Пусть I – нормальный (доаварийный, предшествующий, исходный) режим;

II – режим КЗ;

III – послеаварийный режим.

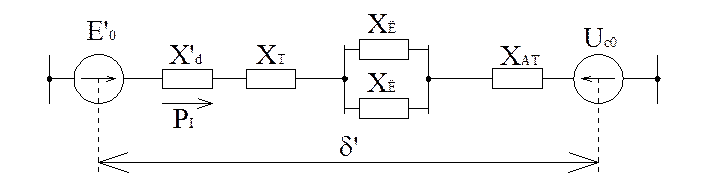
Рис.4.2. Нормальный режим простейшей системы I.

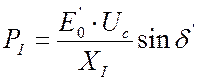,           .            (4.5)

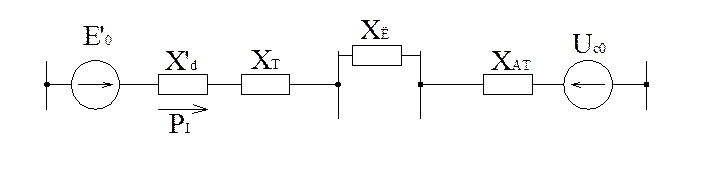
Рис.4.3. Послеаварийный режим простейшей системы III.

,        

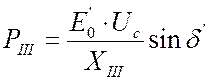.                             (4.6)

Таким образом, из (4.5) и (4.6) получаем: .

При симметричном КЗ мощность в системе будет равна нулю . В режиме несимметричного КЗ в системе кроме токов прямой последовательности протекают токи обратной и нулевой последовательностей. Токи нулевой последовательности на мощность генератора никак не влияют, т.е. их в генераторе просто нет. Токи же обратной последовательности в генераторе есть в несимметричном режиме. Токи обратной последовательности создают поле, вращающееся с частотой , но в обратную сторону, т.е. поле обратной последовательности и ротор генератора перемещаются друг относительно друга со скоростью . В результате взаимодействия поля  и токов, в обмотке возбуждения и во всех металлических частях ротора возникают вращающие моменты  и .

,           ,                                             (4.7)

где  - синхронный момент, но этот момент не сможет раскачать ротор, т.к. он знакопеременный с частотой , т.е.  не влияет на скорость ротора.  - асинхронный момент от токов обратной последовательности не равен нулю, но мал и в упрощенных практических расчетах им можно пренебречь.

Следовательно, при определении мощности генератора в режиме несимметричных КЗ нужно учитывать только токи прямой последовательности, т.е.  следует определять по схеме замещения прямой последовательности.

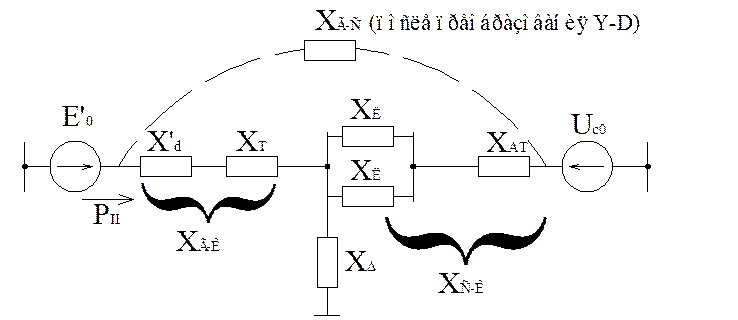
Рис.4.4. Режим КЗ простейшей системы II.

,          ,

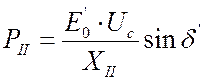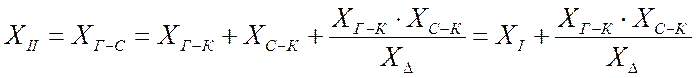.         (4.8)

Т.е. . В такой схеме получается еще, что , следовательно:

.                                                                              (4.9)

Очевидно, что  зависит от вида и места КЗ. Т.к. разница между  и  мала, допускаем, что , поэтому принимаем, что  как и  не изменяется скачком. Погрешность при таком допущении невелика. Изобразим угловые характеристики мощности всех трех режимов (I, II, III) на рис.4.4 и рассмотрим процессы движения ротора при возникновении несимметричного КЗ в начале линии и его последующем отключении релейной защитой.

В предшествующем режиме находились в точке . Произошло КЗ, процесс пошел из точки  на кривую  (мгновенно), а т.к.  мгновенно измениться не может, тогда попадаем в точку . При этом возникает ускоряющий момент, появляется приращение скорости  (, а в нормальном режиме ).

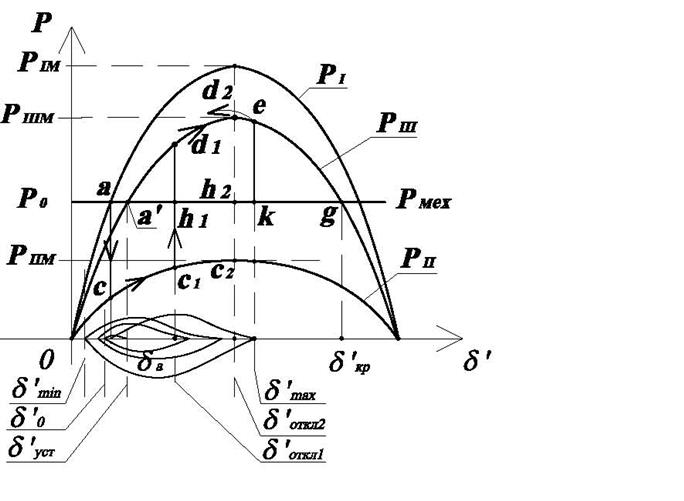
Рис.4.5. Исследование динамической устойчивости простейшей системы.

Некоторое время (0,1-0,2 с) длится аварийный режим, и процесс идет по кривой II, потом КЗ отключается релейной защитой,  и электрическая мощность сразу возрастает, и сразу же избыточный момент меняет знак, т.е. становится тормозящим. Пока скорость  больше , растет, если , , значит и после отключения КЗ пока еще , хотя и снижается, поэтому . После точки, где  () процесс пойдет в сторону уменьшения  и идет по кривой III в обратную сторону. В точке  избыточный момент становится равен нулю, но процесс изменения  не прекращается, т.к. , поэтому  будет снижаться далее. Но как только процесс переходит через , избыточный момент  становится ускоряющим, и скорость начинает расти, и, наконец, становиться равной синхронной , но продолжает расти, т.к.  действует ускоряющий момент , следовательно, снова начинает расти , т.к.  и т.д. И если есть потери мощности, то процесс затухает по спирали (колебательно) под действием   и в точке  образуется новый установившийся режим (см. рис.4.4 и 4.5).

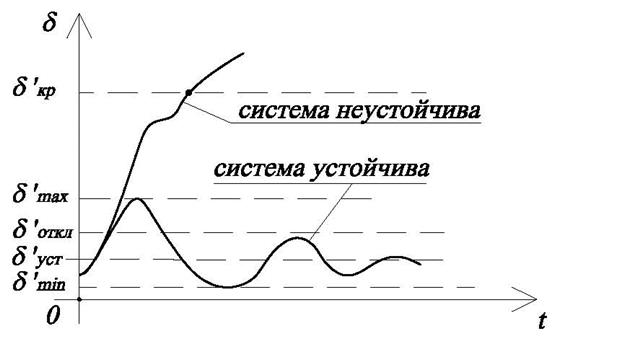
Рис.4.6. Диаграммы устойчивых и неустойчивых систем.

Т.е. в результате КЗ возникает качание генератора (в основном по ,  изменяется не сильно).

Определим теперь  - угол, при котором система еще динамически устойчива.

За время ускорения в режиме КЗ ротор генератора приобретает дополнительную кинетическую энергию  за счет увеличения скорости вращения :

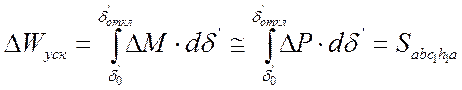,                                  (4.10)

где . Площадка  на рис. 4.4 называется площадкой ускорения . После отключения КЗ скорость вращения ротора  снижается, т.е. ротор теряет дополнительную кинетическую энергию, и при  ротор генератора будет иметь такую же кинетическую энергию, как в исходном режиме, а энергия, потерянная при торможении, тоже может быть выражена площадкой.  Следовательно, энергия, потерянная ротором в процессе торможения, равна энергии, приобретенной в процессе ускорения.

 - это площадка торможения .

, т.е. .                                                    (4.11)

Площадка  - возможная площадка торможения. Пусть время отключения КЗ больше, чем в примере на рис.4.4, т.е.  будет больше. Если , то , а площадка ускорения  и тогда , и поэтому в точке, соответствующей точке ,  этому соответствует , после превышения этого  следует выпадение из синхронизма.

Т.е. в случае, когда отключение КЗ происходит при ,  генератор приходит в точку  со скоростью , и рост  продолжается, а т.к. торможения больше не будет генератор выпадает из синхронизма в сторону увеличения скорости вращения .

При  размах качаний настолько велик, что достигает  и выходит из синхронизма.

Исходя из этого признак динамической устойчивости:

Если возможная площадка торможения больше площадки ускорения (), то ее хватает, чтобы поглотить всю кинетическую энергию, приобретенную за время ускорения, и система устойчива.

Если возможная площадка торможения меньше площадки ускорения (), то генератор успевает проскочить до  и выпадает из синхронизма, т.е. система не устойчива.

Рассмотрим влияние на устойчивость системы различных факторов.