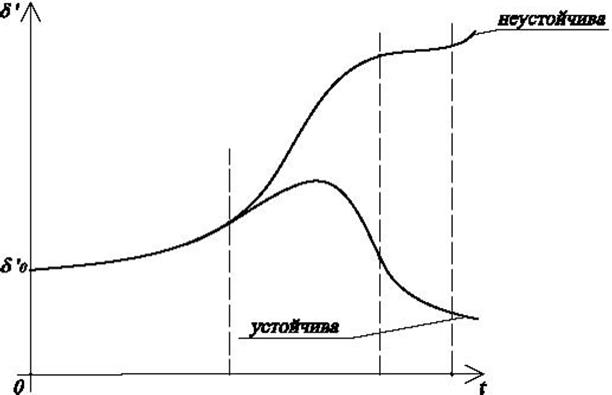
Рис.4.14. Характеристика устойчивой и неустойчивой систем.
Расчет проводится также методом последовательных
интервалов. Разбивку на интервалы надо сделать так, чтобы момент отключения КЗ
(точка с номером ![]() рис.4.14) находился на
границе двух интервалов.
рис.4.14) находился на
границе двух интервалов.
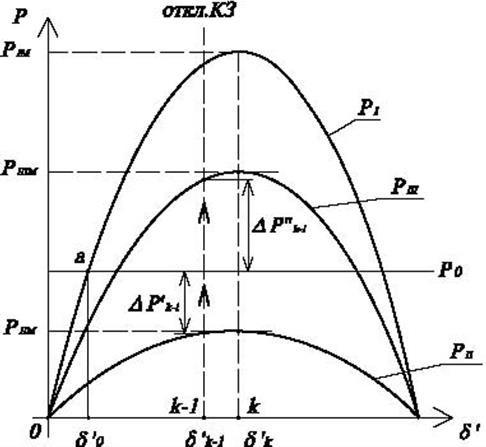
Рис.4.15. Определение зависимости ![]() .
.
Пусть отключение КЗ происходит в начале k-того интервала, тогда:
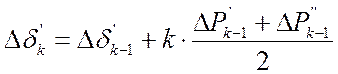 , (4.34)
, (4.34)
![]() ,
, ![]() . (4.35)
. (4.35)
Для последующих интервалов справедливы все ранее записанные выражения.
Есть еще способ применения типовых кривых для определения
характера изменения угла ![]() (т.е.
(т.е. ![]() ).
).
При этом используются кривые ![]() ,
которые получены при решении на ПК дифференциального уравнения
,
которые получены при решении на ПК дифференциального уравнения
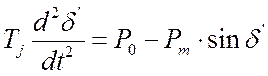 , записанного в
обобщенном виде:
, записанного в
обобщенном виде:
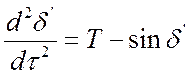 , (4.36)
, (4.36)
с учетом введения новых параметров:
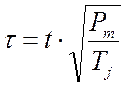 и
и 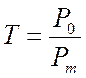 , (4.37)
, (4.37)
где ![]() - время, с;
- время, с;
![]() - расчетное
время;
- расчетное
время;
![]() - амплитуда той
характеристики мощности, которая соответствует начальному режиму;
- амплитуда той
характеристики мощности, которая соответствует начальному режиму;
![]() (или
(или![]() ) – приведенная мощность первичного
двигателя (см. рис.4.15).
) – приведенная мощность первичного
двигателя (см. рис.4.15).
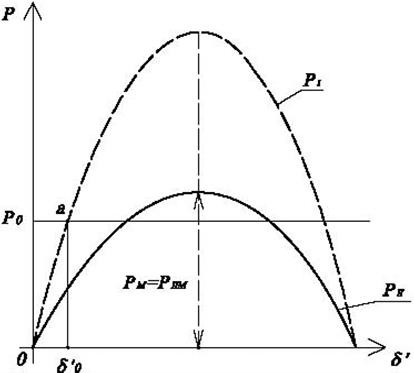
Рис.4.16. Угловые характеристики мощности нормально и аварийного режима.
Аварийных режимов можно рассчитать 2:
1) КЗ;
2) Простое отключение одной из цепей ЛЭП (вывод в ремонт).
Уравнение (4.36) содержит 3 обобщенных параметра ![]() ,
, ![]() ,
, ![]() , в результате решения (4.26) для
различных значений
, в результате решения (4.26) для
различных значений ![]() ,
, ![]() ,
,
![]() были получены кривые
были получены кривые ![]() .
.
Эти типовые универсальные кривые при заданном значении
начального угла ![]() приведены в справочниках в
виде 10 семейств кривых, каждый из которых построен для определенного значения
приведены в справочниках в
виде 10 семейств кривых, каждый из которых построен для определенного значения ![]() (т.е.
(т.е. ![]() )
от 0 до 0,9 через 0,1.
)
от 0 до 0,9 через 0,1.
В качестве образца показаны кривые для ![]() (т.е.
(т.е. ![]() ),
см. рис. 4.16.
),
см. рис. 4.16.
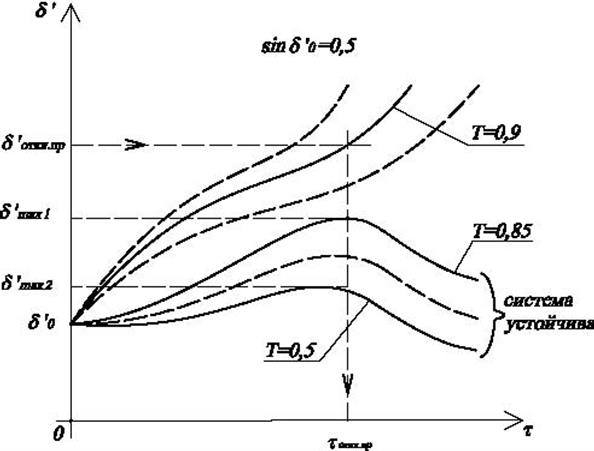
Рис.4.17. Типовые универсальные кривые ![]() для
для ![]() (
(![]() ).
).
В начале расчета надо определить ![]() ,
, ![]() ,
, ![]() , а
, а ![]() задано.
задано.
При помощи типовых кривых ![]() можно
по найденному заранее
можно
по найденному заранее ![]() определить
определить ![]() сначала в виде расчетного времени
сначала в виде расчетного времени ![]() , а далее можно легко перейти ко
времени в секундах согласно выражению:
, а далее можно легко перейти ко
времени в секундах согласно выражению:
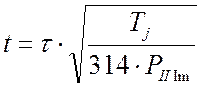 . (4.38)
. (4.38)
Но прежде необходимо выяснить, имеет ли смысл
вычислять ![]() и определять
и определять ![]() .
Для этого нужно вычислить
.
Для этого нужно вычислить ![]() ,
, ![]() , затем:
, затем:
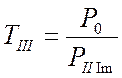 ,
, 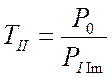 и
и ![]() . (4.39)
. (4.39)
Пусть для полученных значений имеем вид типовых кривых
рис.4.17 а или б, тогда система заведомо неустойчива (а) или заведомо устойчива
(б) и дальнейших расчетов не требуется. В промежуточных случаях (рис.4.17.в)
требуются расчеты по определению ![]() и определение по
кривым
и определение по
кривым ![]() (и
(и ![]() по
(4.38)).
по
(4.38)).
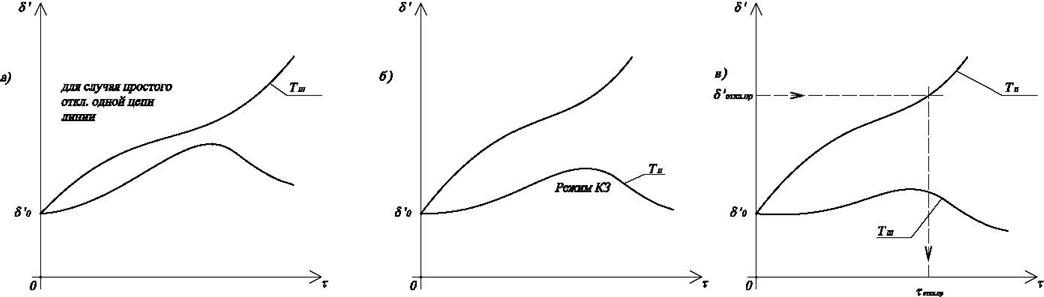
Рис.4.18. Типовые кривые: а – заведомо неустойчивой системы; б – заведомо устойчивой системы; в – неопределенная устойчивость у системы.
Влияние АРВ на динамическую устойчивость
До сих пор мы рассматривали вопросы динамической
устойчивости в предположении отсутствия АРВ у генератора G,
т.е. при построении угловых характеристик мощности ![]() ,
, ![]() предполагалось, что
предполагалось, что ![]() .
.
У генератора с АРВ напряжение возбуждения может изменяться (см. рис.4.15) в случае необходимости (например, при КЗ в сети).

Рис.4.19. Напряжение возбуждения генератора с АРВ.
Предположим, что имеют место следующие условия рис.4.19.
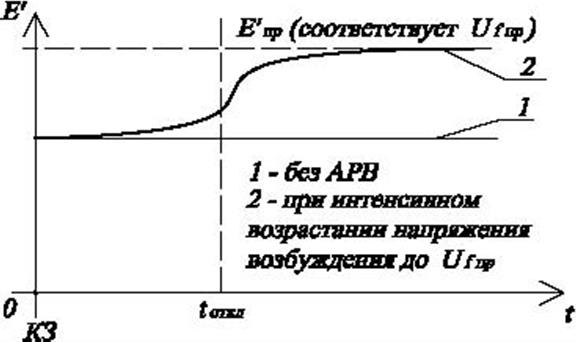
Рис.4.20. ![]() в простейшей
системе с генератором, оснащенным АРВ.
в простейшей
системе с генератором, оснащенным АРВ.
Регулирование возбуждения генератора в смысле эффекта на динамическую устойчивость можно рассматривать качественно см рис.4.20.
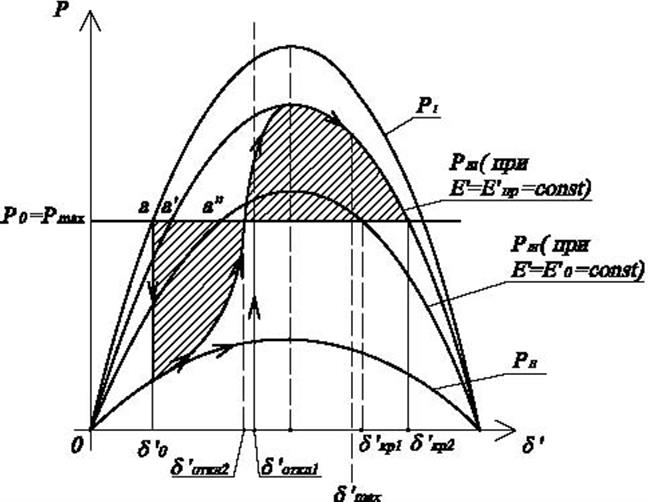
Рис.4.21. Влияние АРВ на динамическую устойчивость.
В начале предположим, что АРВ нет или оно слабое, т.е.
считаем, что ![]() . В этом случае система,
безусловно, неустойчива, т.к.
. В этом случае система,
безусловно, неустойчива, т.к. ![]() . Пусть теперь
. Пусть теперь ![]() растет до
растет до ![]() (до
потолка возбуждения). В этом случае генератор не достигает
(до
потолка возбуждения). В этом случае генератор не достигает ![]() , но достигает
, но достигает ![]() , при котором
, при котором ![]() .
.
В случае (1), когда нет АРВ площадки ![]() и
и ![]() обозначены
штриховкой, в этом случае система неустойчива
обозначены
штриховкой, в этом случае система неустойчива ![]() .
.
В случае (2) при наличии АРВ площадки ![]() и
и ![]() обозначены
жирными линиями. В этом случае система устойчива, т.к.
обозначены
жирными линиями. В этом случае система устойчива, т.к. ![]() .
Таким образом, действие АРВ положительно сказывается на динамической
устойчивости системы.
.
Таким образом, действие АРВ положительно сказывается на динамической
устойчивости системы.
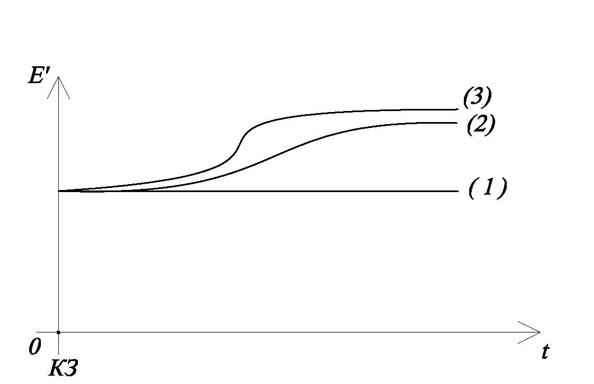
Рис.4.22. Возбуждение генератора с АРВ.
Чем быстрее нарастает возбуждение генератора после возникновения КЗ, тем это лучше с точки зрения динамической устойчивости. Чтобы возбуждение нарастало быстрее потолок возбуждения должен быть дольше, а время меньше. Но это технически сложно, и делать это нужно лишь при большой необходимости.
С другой стороны, нужно иметь в виду, что время
протекания в роторе предельного тока возбуждения ![]() ограничено,
т.е. длительно нельзя поддерживать
ограничено,
т.е. длительно нельзя поддерживать ![]() . Через некоторое
время необходимо возбуждение снизить до
. Через некоторое
время необходимо возбуждение снизить до ![]() ,
при этом из точки
,
при этом из точки ![]() переходим в точку
переходим в точку ![]() (см. рис.2.20).
(см. рис.2.20).
Но если чересчур быстро снизить возбуждение до
нормального значения, то генератор выпадет из синхронизма во втором цикле
качаний при движении в сторону ![]() .
.
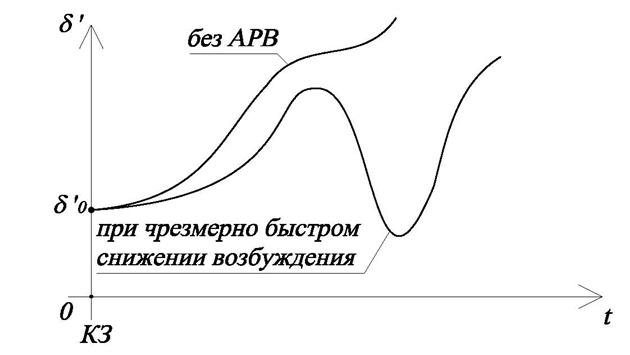
Рис. 4.23. Действие наличия АРВ на устойчивость простейшей системы.
Быстрое увеличение возбуждения при КЗ называется форсировкой возбуждения. Форсировку возбуждения следует держать до тех пор, пока не затухнут качания, раньше снижать опасно из соображений динамической устойчивости.
Лучше всего, чтобы с ростом угла ![]() росло бы и возбуждение, при снижении
угла
росло бы и возбуждение, при снижении
угла ![]() , возбуждение бы тоже уменьшилось.
При новом возрастании угла
, возбуждение бы тоже уменьшилось.
При новом возрастании угла ![]() форсировка бы
снова увеличилась, таким регулированием лучше обеспечивается динамическая
устойчивость, быстро гасятся качания
форсировка бы
снова увеличилась, таким регулированием лучше обеспечивается динамическая
устойчивость, быстро гасятся качания ![]() .
.
Определение запаса динамической устойчивости
Запас динамической устойчивости системы определяется тремя способами:
1) Руководствуясь правилом площадей:
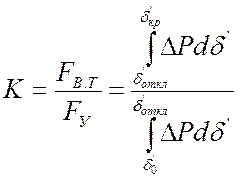 . (4.40)
. (4.40)
![]() должен
быть больше 1 для обеспечения динамической устойчивости.
должен
быть больше 1 для обеспечения динамической устойчивости.
2) По ухудшению начального режима станции.
Принимаем в начале ![]() ,
делаем расчеты при
,
делаем расчеты при ![]() , допустим все хорошо.
, допустим все хорошо.
Далее берем ![]() , пусть снова
система устойчива, берем
, пусть снова
система устойчива, берем ![]() и т.д.
и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.