Методические рекомендации к лабораторным работам: "Проверка работоспособности телеметрического выхода счетчика", "Комплекс технических средств «Энергия»", "Программирование микропроцессорного устройства «Энергия–микро»", страница 6

F₁=k×Ф_I×I^’_U.

Заметим, что в этом случае усилие будет максимальным так .как магнитный поток Ф_I и ток 1^/_U пространст­венно сдвинуты на угол 90° (ось магнитопровода – маг­нитного потока перпендикулярна к плоскости диска), ток I^’_U находится в фазе с магнитным потоком. Так как в этот момент Ф_U=0 и I^’_I=0, то и F₂=0

Через промежуток времени p/2w  поток Ф_U достигает максимума, а поток Ф_I переходит через нуль (положе­ние 2). В этот момент взаимодействуют Ф_U и I^’_I , созда­вая усилие F₂, также согласно «правилу левой руки» направленное по часовой стрелке; при этом F₁=0; F₂=k₂×Ф_U×I^’_I.

Через последующий промежуток времени p/2w  (поло­жение 3) магнитный поток Ф_I снова достигает максиму­ма, но в противофазе, а поток Ф_U переходит через нуль. Взаимодействие Ф_U с током I^’_I создает силу F₁, также направленную по часовой стрелке: F₁=k₁×Ф_I×I^’_U , и в этот момент F₂=0.

В четвертый момент (положение 4) через следующий промежуток p/2w магнитный поток Ф_U достигает отрица­тельного максимума, а Ф_I переходит через нуль. Сила F₂ взаимодействия Ф_U с  I^’_I также направлена по часовой стрелке: F₂=k₂×Ф_U×I^’_I. F₁==0. Далее цикл повторя­ется. В промежутках времени между рассмотренными экстремальными моментами возникают два усилия F₁ и F₂, направленные в противоположные стороны, как это видно, например, на рис. 1.3.3. Разностная сила в какой-то момент времени t будет направлена также по часовой стрелке, поскольку опережающий поток, например +Ф_I, взаимодействуя с 1'_U, создает большую силу, нежели отстающий поток Ф_U с током I^’_I. Это видно из рис. 1.3.4,в, где в момент t поток Ф_I и ток 1'_U от амплитудных зна­чений только начинают уменьшаться по синусоидально­му закону, а поток Ф_U и ток I'_I только начинают увели­чиваться от нулевого значения (на рисунке ординаты Ф_I и 1'_U для момента времени t больше ординат Ф_U и I'_I}. Отсюда следует правило, что результирующая электро­магнитная сила направлена в сторону от следа полюса опережающего магнитного потока к следу полюса от­стающего магнитного потока. Следовательно, на рис. 1.3.3 направление результирующей силы будет от полюса +Ф_I к полюсу Ф_U и от полюса Ф_U к полюсу минус Ф_I. Из рис. 1.3.4,г видно, что электромагнитная сила F пульсирует, достигая нулевого значения через промежутки p/2w ког­да F₁=  –  F₂

Из сказанного следует, что максимальная результи­рующая электромагнитная сила возникает в момент, когда одна из составляющих сил равна нулю, и опреде­ляется взаимодействием одного магнитного потока с сопряженным с ним током  в диске.

1.3.1. Вращающий момент индукционного счетчика. Определим среднее значение пульсирующей электро­магнитной результирующей силы, создающей вращаю­щий момент диска.

Мгновенное значение будет равно:

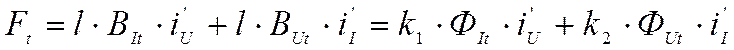где l – длина активной части контура тока в диске; В_It, В_Ut  –  мгновенные значения средней индукции магнитно­го потока последовательной и параллельной цепей; Ф_It, Ф_Ut – мгновенные значения магнитных потоков по­следовательной и параллельной цепей, равные произве­дению средней индукции на площадь потока; i'_I, i'_U –  мгновенные значения токов в диске, наведенные магнит­ными потоками последовательной и параллельной цепей; k₁, k₂. – постоянные коэффициенты.

Так как магнитные потоки и наведенные ими токи изменяются по синусоидальному закону с частотой сети, то их мгновенные значения можно выразить в амплитуд­ных значениях. При этом, полагая сопротивление диска активным, учтем, что токи в диске будут совпадать по фазе с наведенной в нем э. д. с. и, следовательно, отста­ют от породивших их магнитных потоков на 90°. Вектор­ная диаграмма токов в диске изображена на рис. 5; пользуясь ею, мгновенное значение электромагнитной силы можно представить следующим образом:

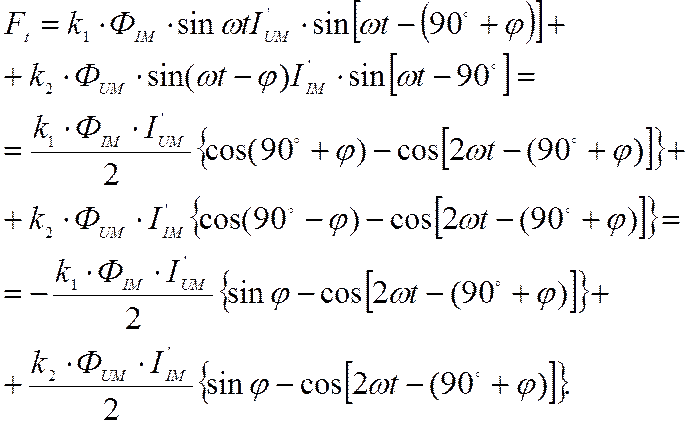Для преобразования использована тригонометрическая формула:

За исходный принят вектор потока Ф_IM от которого откладыва­лись по часовой стрелке фазовые углы со знаком минус.

Рассматривая полученное выражение, устанавливаем, что каждое слагаемое состоит из постоянного члена (не содержащего wt) и переменного, изменяющегося по гар­моническому закону (по косинусоиде). Так как среднее значение ординат косинусоиды за период равно нулю, то очевидно, что среднее значение результирующей силы будет равно постоянной части:

Так как наведенные в диске токи пропорциональны породившим их магнитным потокам, т. е.
 то среднее значение результирующей магнитной силы, как это видно на рис. 4,г, будет равно среднему значе­нию одной из составляющих сил F₁ или F₂, т. е. момент вращения диска, равный произведению ре­зультирующей маг
нитной силы F на радиусе ее прило­жения, будет равен:

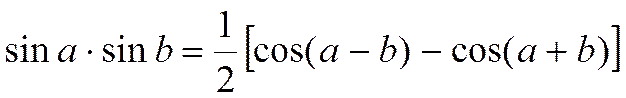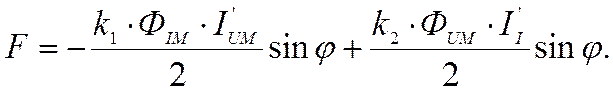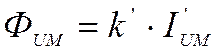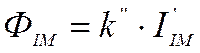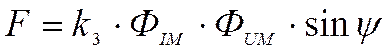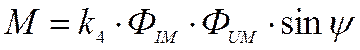Очевидно, что максимальный момент будет тогда, когда siny=1, т. е. y=90°. Таким образом, для счетчи­ка активной энергии обязательным условием является 90-градусный сдвиг между рабочим потоком цепи на­пряжения и потоком 'последовательной цепи. Если оба магнитопровода не насыщены, то поток последователь­ной цепи Ф_I пропорционален току нагрузки I, проходя­щему :по токовой цепи, т. е. Ф_IM=k^’I.

Поток Ф_общ в параллельной цепи, частью которого является Ф_U, пропорционален наведенной обратной э. д. с., равной приложенному к параллельной цепи на­пряжению U, т. е.

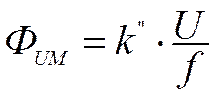Тогда момент, вращения диска можно будет выра­зить через значения тока и напряжения сети:

M=kIU siny.

В общем случае y=90°+j, где j – угол между то­ком и напряжением, подводимым к счетчику, и, следова­тельно,

M=kIU sin(90°+j)=kIU cosj=kP

Таким образом, мы убедились в том, что момент вра­щения диска пропорционален мощности сети, расход электроэнергии в которой измеряется счетчиком.

1.3.2. Противодействующий и дополнительные моменты. Момент вращения, создаваемый результирующей электромагнитной силой, приведет во вращение диск. Частота вращения диска будет определяться частотой сети и числом пар полюсов и практически не будет за­висеть от нагрузки.