Методические рекомендации к лабораторным работам: "Проверка работоспособности телеметрического выхода счетчика", "Комплекс технических средств «Энергия»", "Программирование микропроцессорного устройства «Энергия–микро»", страница 11

На рис. 1.3.11 приведены принципиальные схемы вклю­чения однофазного счетчика СО (СОУ) с указанием по­лярности измерительных трансформаторов. Вторичные обмотки трансформатора тока и трансформатора напряжения в целях безопасности заземлены. Принципиально безразлично, что заземлять – начала или концы обмо­ток измерительных трансформаторов. Векторная диаг­рамма счетчиков здесь и для последующих схем постро­ена для токов и напряжений на зажимной колодке счетчика. Для косвенного включения векторные диаг­раммы соответствуют вторичным токам и напряжениям, что в масштабе коэффициентов трансформации измери­тельных трансформаторов соответствует и первичным токам, и напряжениям. При построении векторных диа­грамм трехфазных счетчиков за оси координат будем всегда принимать симметричную звезду фазных напря­жений трехфазной системы.

Принципиальная  схема  включения трехфазного счетчика активной энергии для непосредственного вклю­чения в трехфазную трехпроводную сеть (тип САЗ) при­ведена на рис. 1.3.12,а, б. Эту схему мы рассмотрим под­робно, поскольку она является основной при измерении активной энергии в трехфазных установках без нулево­го провода, и на ее примере проследим построение век­торной диаграммы включения счетчика.

Как видно из схемы, токовая цепь первого измери­тельного элемента 1 счетчика включена в фазу 1, при­чем генераторный зажим Г присоединен со стороны пи­тания (передача энергии на схеме слева направо). Цепь напряжения этого элемента включена на линейное на­пряжение между фазами 1 и 2, и ее однополярный за­жим 1 присоединен к фазе 1. Токовая цепь второго эле­мента 2 включена в фазу 3 генераторным концом Г со стороны питания. Цепь напряжения этого элемента включена между фазами 3 и 2, а ее однополярный за­жим присоединен к фазе 3.

Напомним, что при построении векторных диаграмм условно принимаются потенциалы концов обмоток трех­фазного источника тока, соединенного в звезду, выше потенциалов начал обмоток, потенциал которых для симметричной системы равен нулю. Соответственно это­му считают положительными направлениями векторов направления от нулевого или от низшего потенциала к высшему, и тогда конец вектора, обозначенный острием стрелки, будет положительным. Вектор обозначается двумя индексами, из которых первый обозначает конец вектора (острие стрелки), а второй – начало. Если начало вектора имеет условный нулевой потенциал, то обычно второй индекс опускается. Например, фазное напряжение фазы 1 обозначается U₁₀ или U₁. Линейное напряжение между  фазами 1 и 2, являющееся геомет­рической разностью этих двух фазных напряжений, обо­значается U₁ – U₂=U₁₂,, в то же время U₂ – U₁=U₂₁ явля­ется таким же вектором, но имеющим противоположное направление (повернут на 180°).

Так как измеряемая электроэнергия пропорциональ­на мощности нагрузки, то в дальнейшем при выводе ос­новных соотношений  будем оперировать с мощностью.

Из векторной диаграммы видно, что вращающий мо­мент первого -

и второго элемента

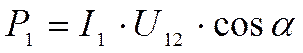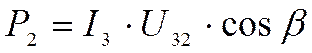измерительного элемента пропорционален мощности 

Алгебраическая сумма этих двух мощностей, как показано ниже, равняется мощности трехфазной урав­новешенной системы (без нулевого провода) при любой нагрузке фаз, любой асимметрии фазных напряжений и любом чередовании фаз.

Для доказательства этого выразим измеряемые мощ­ности в мгновенных значениях.

Как известно, мгновенные значения сопряженных токов и напряжений всегда совпадают по фазе для лю­бого момента времени (рис. 1.3.14,г). Тогда мгновенное зна­чение мощности р будет равно произведению мгновен­ных значений напряжения и и тока i.

 Для рассматри­ваемой схемы

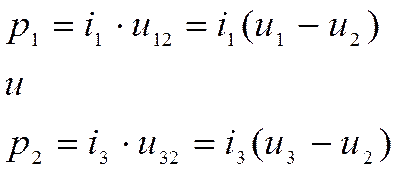Так как для трехфазной уравновешенной системы всегда i₁+i₂+i₃=0 и, следовательно, i₂=  – (i₁+i₃),

то

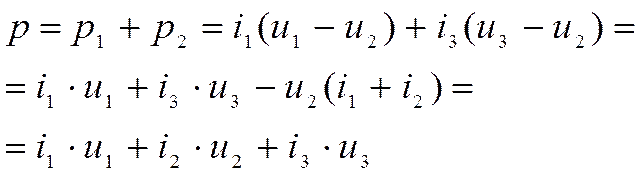т. е. мгновенная мощность трехфазной уравновешенной системы равна сумме мгновенных мощностей ее фаз.

Для перехода от мгновенных значений к действую­щим учтем, что мгновенные значения напряжений, и то­ков могут быть выражены в виде синусоидальных функции, а именно:

u=U_Msinvt   и  i=I_Msin(vt+j)

где U_M и I_M максимальные (амплитудные) значения напряжения и тока; j – угол сдвига фаз между напряжением и током, w – угловая частота переменного тока, w=2pf=2p/T; f – частота переменного тока; Т – период синусоиды.

Тогда мгновенная мощность, выражаемая через дей­ствующие значения тока и напряжения, будет равна:

где U и I – действующие (среднеквадратичные) значе­ния напряжения и тока;

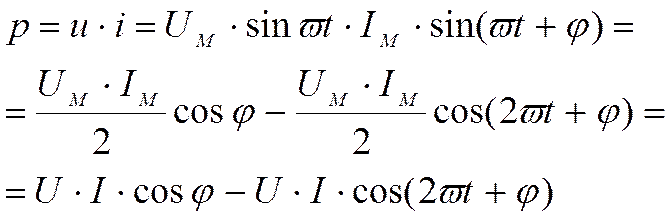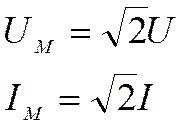 Как видно из последнего выражения, мгновенная мощность состоит из двух слагаемых: из постоянной ча­сти UI cosj, представляющей среднюю мощность за период, и переменной части UI cos (2vt+j), имеющей амплитуду UI и изменяющейся по синусоидальному за­кону, но с двойной частотой. Среднее значение этой со­ставляющей мощности за период, как известно, равно нулю.

Таким образом, вращающий момент измерительного элемента счетчика пропорционален средней мощности P=UIcosj.

Заменяя мгновенные значения токов и напряжений действующими значениями, получаем:

Р = P₁+P₂ = U₁I₁cosj₁+ U₂I₂cosj₂ +U₃I₃cosj₃,

т. е. вращающий момент двухэлементного трехфазного счетчика активной энергии, включенного в трехфазную сеть без нулевого провода, пропорционален активной мощности трехфазного тока независимо от величины на­грузки отдельных фаз и фазового сдвига тока в каждой фазе и принципиально не зависит от порядка следова­ния фаз.

Векторная диаграмма включения двухэлементного счетчика для наглядности построена для случая симмет­ричной и равномерной нагрузки. Заметим, что в сетях при нормальном режиме звезда фазных (и, следователь­но, междуфазных) 'напряжений практически всегда сим­метрична (сдвиги между фазами 120°). Для этого случая момент вращения первого элемента будет пропорционален 

и второго элемента

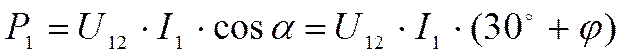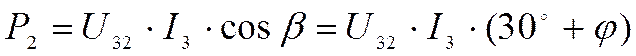При равномерной нагрузке U₁₂=U₃₂=U и I₁=I₃=I тогда суммарный момент счетчика пропорционален мощности нагрузки: