Исследования и оценка параметров надежности и безотказности автомобилей: Лабораторные работы. Часть ІІІ (Примеры выполнения работ), страница 5

Предположим, что отказы, зафиксированные в этой таблице распреде-лены по закону Вейбулла. Построим вероятностную шкалу, для чего составим вспомогательную таблицу (табл. 4.5)

Определим ширину графика L и масштаб К_x по оси х. Наименьшее значение наработки t_min=6, а t_max=117

                              lgt_max- lgt_min= lg117- lg 6=1,29.

Выберем К_х=100 мм. Тогда из формулы для К_х,  L=129 мм. Подсчитаем значение x_i =lgt_i и внесем их в таблицу

Подсчитаем S_x (t_i)=К_х x_i =100 lgt_i (мм).

Внесем в таблицу значения 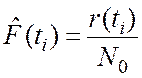  из табл.8.1.

Выберем размер графика по высоте Н =200 мм.

С помощью табл. 8.2 подсчитаем значения

S_y = 200/8,84)·у (мм).

Промежуточные значения можно с некоторой погрешностью получить интерполированием или рассчитать  по формуле :

                                           

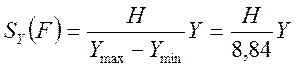
Построим вероятностную шкалу, отложив, но осям (t) и  соответствующие отрезки S_x(t_i) и S_y(F).

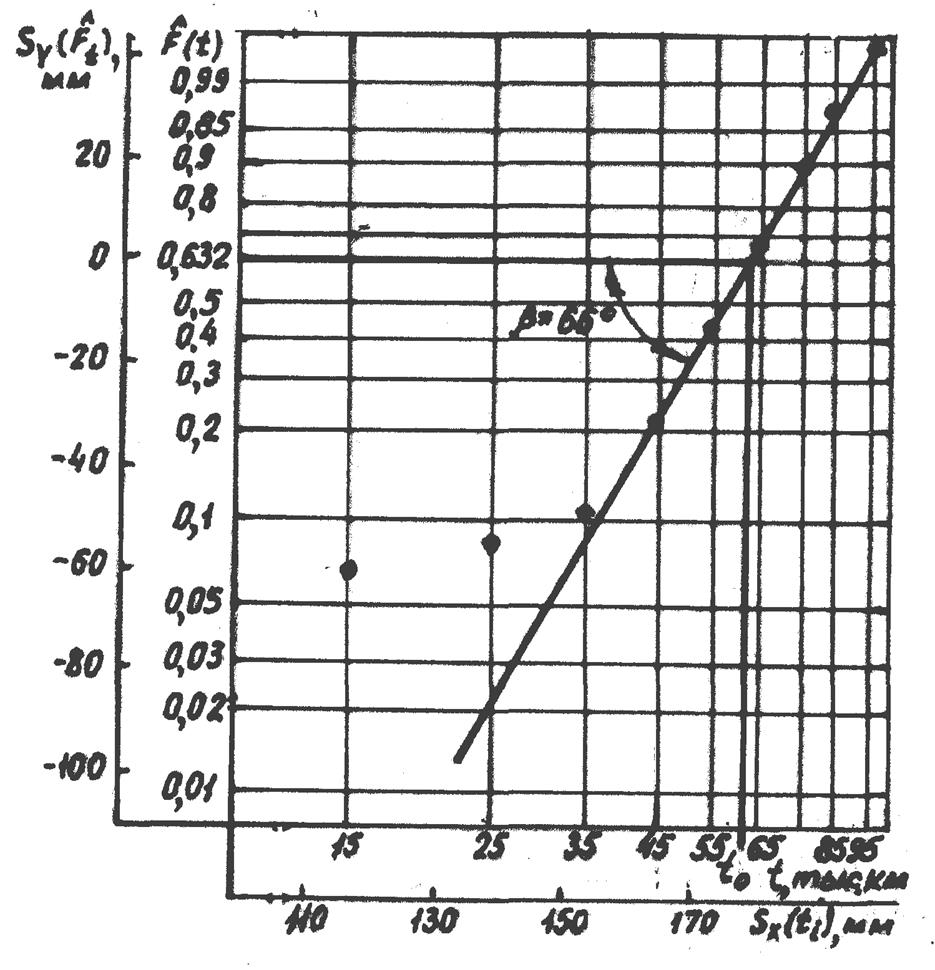
Найдем пересечения значений t_i и F(t_i) из табл. 4.5 и пометим их точками. Проведем прямую линию таким образом, чтобы точки были как можно ближе к этой прямой (равное количество по обе ее стороны). Все это проделано на рис. 12, из которого следует, что, начиная с наработки t=35 тыс, км, прямая соединила почти все точки. Это свидетельствует о том, что сделанные нами предположения о выборе закона распределения, по крайней мере начиная с этой наработки, правильны. Можно предположить, что в начальный период, т. е. при наработке до 25 тыс, км, отказы распределяются по экспоненциальному закону.

Полученный график позволит нам определить  параметры распределения и подсчитать показатели надежности. 

Из выражения Y=(8,84/Н)S_Y(F)  и из формулы    x=(1/К_х )S_x (t) подста-вим  в выражение : y=2,303bx+C, где коэффициент при х есть угловой коэффициент

                ;     ;

                                       ;                                                 

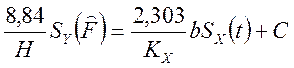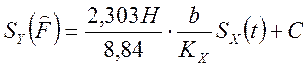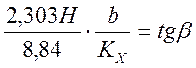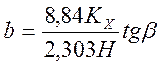
Определив параметр b распределения Вейбулла, находим второй параметр t₀  из выражения 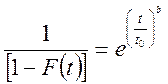 . Если t = t₀, то 1/ [1 –F(t_σ)]=e  и тогда  F(t₀)=(e-1)/e=0,6321.

 Рис. 4.5. Определение параметров распределения Вейбулла с помощью вероятностной сетки

Таким образом, t₀  есть значение t, когда F (t) =0,6321.

Учитывая, что  lgt₀ =S_x (t₀)/К_{x .}  Замерим S_x (t₀) = 180 мм  и угол β= 66 ⁰ (рис. 4.5).

 Тогда: 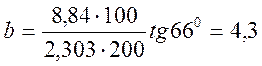; lgt₀=180/100 =1,8; t₀= 10^1,8 ≈ 63 тыс. км.

Для рассматриваемого примера закон Вейбулла  принял  следующий конкретный вид:

                        

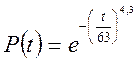
Теперь можно рассчитать любые параметры распределения и показатели надежности, в результате получим:

t_СР=57 тыс. км; D=228тыс.км²; σ=15,1 тыс. км ; ν=0,26.

Аналогично строятся координатные сетки для нормального и экспоненциа-льного распределения.

Таким образом, с помощью вероятностных шкал с достаточной для практики точностью можно определить, какому закону распределения следуют полученные из наблюдений данные, и на этой основе найти параметры распределения и другие показатели надежности.

Лабораторная работа  №9

Определение вероятности безотказной работы при заданной наработке

Цель работы:

  Определить:

- вероятность безотказной работы ;

-  плотность вероятности наступления отказов ;

-  вероятность отказа ;

-  интенсивность потока отказов ;

-  среднюю наработку до первого отказа t_ср;

-  дисперсию D;

-  среднее квадратичное отклонение  ;

-  коэффициент вариации V.

Исходные данные:

           Путем обработки данных об отказах изделия выявлено, что распреде-ление отказов происходит по закону Вейбулла с параметрами:

t₀  -  параметр масштаба ;  b - параметр формы   при заданной наработке  

Решение:

1. Найдем вероятность безотказной работы по формуле для закона Вейбулла:

,

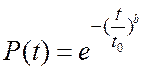где - основание натуральных логарифмов

=

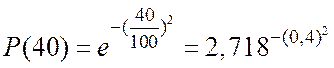2. Вероятность отказа      

3. Плотность вероятности наступления отказа  по формуле для закона Вейбулла равна:

        

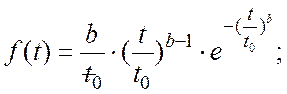
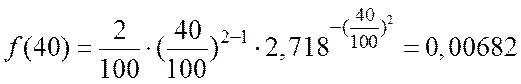
4.  Интенсивность отказов  равна:

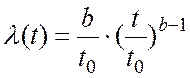    или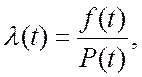        

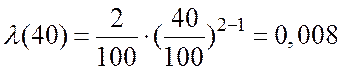
5. Средняя наработка до первого отказа  по формуле закона Вейбулла будет равна:

 ,

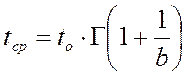где буква  в количественных характеристиках закона Вейбулла обозначает гамма функцию ( таблица 1 приложения).

Для условий нашей задачи 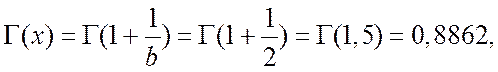  тогда

6. Дисперсия по формуле для закона Вейбулла равна:

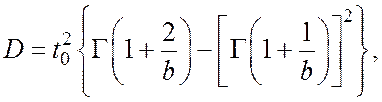  т.е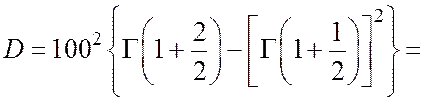   

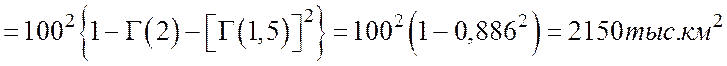
7. Среднее квадратичное отклонение    

8. Коэффициент вариации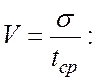  

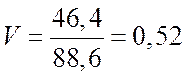
 9. Выводы:

Полученные  расчетные параметры подтверждают правильность утверждения о распределении ПН в соответствии с законом Вейбулла

Лабораторная работа № 10

Определение оптимального ресурса машины и уровня затрат на запасные части

Цель работы:

1. Определить теоретические затраты на запасные части С_зч(t) для данной машины по интервалам наработки.

         2 Рассчитать оптимальный ресурс t_р машины графическим и аналитическим способами.

3 Спрогнозировать расход на запасные части за период наработки до  оптимального ресурса С ^Σзч (t_р).

4. Произвести анализ изменения суммарных затрат на запасные части

С ^Σзч (t_р).

5. Исходные данные в табл. 10.1

Таблица 10.1

Удельные фактические затраты на запасные части-     Сзч (t), (руб/м.ч) по интервалам наработки, м.ч						Сумма коэффиц. А+В+С	Стоимость машины   С0 руб.
0 2000	2000 4000	4000 6000	6000 8000	8000 10000	10000 12000
0,015	0,030	0,070	0,090	0,15	0,15	3,0	22400

Решение:

1. Учитывая, что необходимые затраты C_пн(t), связанные с приобретением запасных частей, с оплатой труда производственного персонала и материалов, а также с компенсацией простоев при известной стоимости объекта, имеются, можно записать:C_пн(t)=C_зч(t)+C_тр(t)+C_м(t)+C_прост(t),

где С_пн(t) – удельные затраты,  связанные с эксплуатацией машины в течение определенного интервала времени ;

C_тр(t) - удельные затраты, связанные с оплатой труда производственного  персонала в течение  той же наработки;

C_м(t)-  удельные затраты на приобретение материалов при той же наработке;

C_прост(t) –удельные затраты, связанные с компенсацией простоев.

Преобразуем правую часть уравнения, разделив почленно, получим:   

    С_пн(t) = С_зч(t)·[1+ С_тр(t) / C_зч(t)+ С_м(t) / C_зч(t)+ С_прост(t) / C_зч(t) ]          

          Сотношения:  С_тр(t) / C_зч(t);   С_м(t) / C_зч(t);   С_прост(t) / C_зч(t);    обозначим соответственно А, В и С, тогда:

                              С_пн(t) = С_зч(t)·(1+ А+В+ C)= 4 С_зч(t)