Цель работы:
1.Определить:
-
частость ![]() ;
;
-
вероятность наступления отказа ![]() ;
;
-
вероятность безотказной работы ![]() ;
;
-
плотность вероятности наступления
отказа![]() ;
;
-
интенсивность отказов ![]() ;
;
- среднюю наработку до первого отказа tср.
2. Оценить рассеивание результатов:
-
средним квадратичным отклонением ![]() ;
;
-
средним арифметическим
отклонением ![]() ;
;
- дисперсией D;
-
коэффициентом вариации ![]() .
.
3. Построить гистограмму распределения числа n,
частости ![]() и плотности отказов
и плотности отказов ![]() в зависимости от наработки t.
в зависимости от наработки t.
Исходные данные:
N0=105, ![]()
tmin=6 тыс.км,
tmax=117 тыс.км
Решение:
1.Определим диапазон наработок R, внутри которого имели место отказы:
![]()
![]() .
.
2. Вычислим длину интервала по формуле:
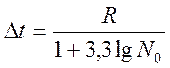 ,
,
где
![]()
![]() -
число испытываемых изделий
-
число испытываемых изделий
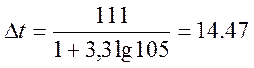
![]() .
.
Принимаем ![]()
Для определения количества интервалов, зададимся левой
![]() и правой
и правой 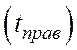 границами
наработок. Примем
границами
наработок. Примем ![]() а
а ![]()
Тогда число интервалов будет равно:
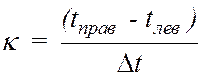 ;
;
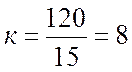
4. Пронумеруем интервалы от ![]() и
впишем их в таблицу 1.1. Найдем середины каждого интервала
и
впишем их в таблицу 1.1. Найдем середины каждого интервала ![]() .
.
5. Впишем в соответствующие графы число изделий ![]() , отказавших внутри каждого
интервала. Это число называется весом.
, отказавших внутри каждого
интервала. Это число называется весом.
6. Подсчитаем накопленное число отказов ![]() как сумму отказов в интервалах, т.е.
как сумму отказов в интервалах, т.е.
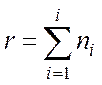 . Результаты вносим в таблицу 2.1.
. Результаты вносим в таблицу 2.1.
Все результаты дальнейших вычислений мы также впишем в соответствующие графы таблицы.
7. Определим число оставшихся работоспособными
объектов к моменту ![]() по формуле:
по формуле:
![]()
8. Вычислим частость ![]() -
относительную долю отказов в интервале:
-
относительную долю отказов в интервале:
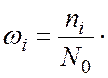
9. Найдем вероятность наступления отказа
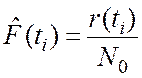
10. Определим вероятность безотказной работы:
![]()
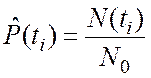
11. Подсчитаем плотность вероятности наступления отказа:
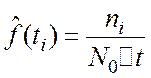
12.
Вычислим интенсивность отказов 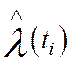 как отношение
числа отказавших объектов в единицу наработки к числу объектов, безотказно
работающих к данному моменту наработки:
как отношение
числа отказавших объектов в единицу наработки к числу объектов, безотказно
работающих к данному моменту наработки:
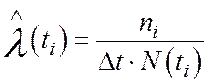 или по формуле:
или по формуле: 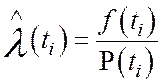 .
.
13. По данным таблицы определим среднюю наработку до 1-ого отказа:
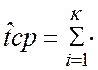
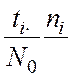 ,
,
где
![]() – число интервалов,
– число интервалов, ![]() - середина интервала,
- середина интервала,![]() - вес.
- вес.
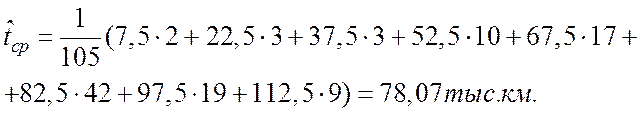
14. Определим характеристики рассеивания.
![]() Среднее арифметическое отклонение
Среднее арифметическое отклонение![]() :
:
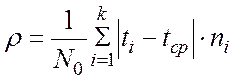
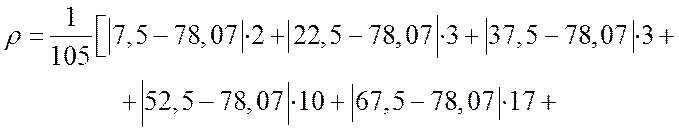
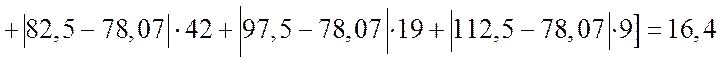
![]() .
.
15. Найдем дисперсию Dпо формуле:
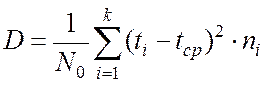
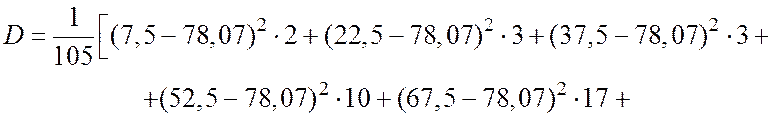
![]()
16.
Среднее квадратичное отклонение ![]()
![]()
![]() .
.
17. Коэффициент вариации 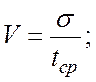
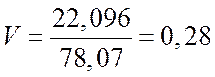 .
.
18. Построим гистограмму распределения числа n,
частости![]() и плотности
и плотности ![]() в
зависимости от наработки
в
зависимости от наработки ![]()
Выводы:
1. Определены:
-
частость ![]() ;
;
-
вероятность наступления отказа ![]() ;
;
- вероятность безотказной работы ![]() ;
;
- плотность вероятности наступления отказа![]() ;
;
-
интенсивность отказов ![]() ;
;
- средняя наработка до первого отказа tср.
Таблица 2.1
|
Определяемый параметр |
Обозначение и формулы расчета |
Номера интервалов наработки |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
Границы интервала наработки, тыс.км |
- |
0-15 |
15-30 |
30-45 |
45-60 |
60-75 |
75-90 |
90-105 |
105-120 |
|
Значение середины интервала, тыс.км |
|
7,5 |
22,5 |
37,5 |
52,5 |
67,5 |
82,5 |
97,5 |
112,5 |
|
Число отказов в интервале (вес) |
|
2 |
3 |
3 |
10 |
17 |
42 |
19 |
9 |
|
Накопленное число отказов |
|
2 |
5 |
8 |
18 |
35 |
77 |
96 |
105 |
|
Число работоспособ-ных объектов к
моменту |
|
103 |
100 |
97 |
87 |
70 |
28 |
9 |
0 |
|
Частость |
|
0,019 |
0,0286 |
0,0286 |
0,0952 |
0,1619 |
0,4 |
0,1809 |
0,0857 |
|
Вероятность наступления отказа |
|
0,019 |
0,048 |
0,076 |
0,171 |
0,333 |
0,733 |
0,914 |
1,0 |
|
Вероятность безотказной работы |
|
0,981 |
0,952 |
0,924 |
0,829 |
0,667 |
0,267 |
0,086 |
0,0 |
|
Плотность вероятности наступления отказа |
|
0,0013 |
0,0019 |
0,0019 |
0,0063 |
0,0108 |
0,0267 |
0,0121 |
0,0057 |
|
Интенсивность отказов |
|
0,0013 |
0,0019 |
0,0021 |
0,0076 |
0,0162 |
0,1 |
0,1407 |
- |
![]() Значок
показывает, что подсчитанный результат получен из статистической обработки
опытных данных, т.е. из наблюдений за выборкой.
Значок
показывает, что подсчитанный результат получен из статистической обработки
опытных данных, т.е. из наблюдений за выборкой.
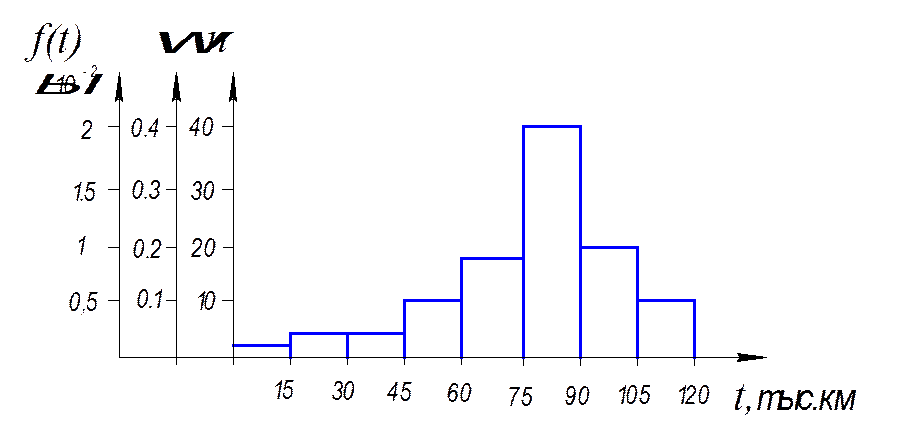 Рис. 2.1. Гистограмма
распределения числа n, частости
Рис. 2.1. Гистограмма
распределения числа n, частости ![]() и плотности
и плотности ![]() отказов
в зависимости от наработки
отказов
в зависимости от наработки ![]()
2 Оценено рассеивание результатов:
- средним квадратичным отклонением ![]() ;
;
- средним арифметическим отклонением ![]() ;
;
- дисперсией D;
- коэффициентом вариации ![]() .
.
3. Построена гистограмма
распределения числа - n,
частости - ![]() и плотности отказов -
и плотности отказов - ![]() в зависимости от наработки t.
в зависимости от наработки t.
4. Полученные результаты свидетельствуют о нормальном распределении случайных величин.
Определение срока службы сопряжения
Цель работы:
1. Определить износ за время нормальной эксплуатации – δ2.
2. Вычислить период нормальной эксплуатации - t2.
3. Определить период приработки – t1.
4. Определить срок службы сопряжения – t.
Исходные данные:
![]()
![]()
![]()
![]() .
.
Решение:
1.
По подобию фигур из прямоугольного треугольника найдем -![]()
 |
![]()
![]() .
.
2.
Вычислим период нормальной эксплуатации ![]()
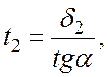 тогда
тогда 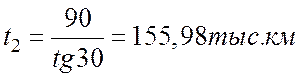 .
.
3.
Определим период приработки ![]() из условия
задачи:
из условия
задачи:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.