Машиностроение \ Основы теории надежности и диагностики

Исследования и оценка параметров надежности и безотказности автомобилей: Лабораторные работы. Часть ІІІ (Примеры выполнения работ), страница 4

Графический метод определения оценок параметров распределения (построение вероятностной бумаги)

Цель работы:

Методом построения вероятностной сетки (бумаги) определить закон распределения параметров надежности.

Исходные данные: использованы из лабораторной работы № 2

Оценка параметров распределения производится по опытным данным. По ним же определяется, какому закону распределения соответствуют эти данные.

Путем несложных преобразований функцию F(t) можно в прямоуголь-ной системе координат с неравномерными шкалами представить в виде пря-мой линии. В этом случае визуальное сравнение эмпирических данных с предполагаемым теоретическим может быть сделано с достаточной для практики точностью. Прямоугольная координатная сетка с измененным масштабом по осям носит название вероятностной сетки или вероятностной бумаги.

Рассмотрим метод построения вероятностной сетки для распределения Вейбулла на примере данных табл.8.1.

Представим функцию F(t) из табл.8.1 в виде 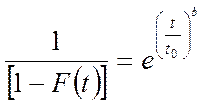и дважды прологарифмируем:

1п1п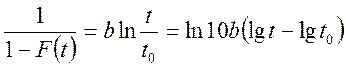

1п1п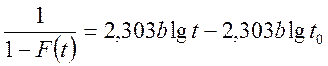 Обозначим: =y; lgt=x ; -2,303 blgt₀ =C.

Тогда: y=2,303bx+C,

т. е. получена линейная зависимость. Теперь построим координатную сетку, на которой по оси ординат будут отложены отрезки, пропорциональные х, а по оси абсцисс — пропорциональные у, Выражение y=2,303bx+C представ-лено в виде прямой линии.

Таблица 8.1(таб.2.1)

Определяемый параметр	Обозначение и формулы расчета	Номера интервалов наработки
Определяемый параметр	Обозначение и формулы расчета	1	2	3	4	5	6	7	8
Границы интервала наработки, тыс.км	-	0-15	15-30	30-45	45-60	60-75	75-90	90-105	105-120
Значение середины интервала, тыс.км		7,5	22,5	37,5	52,5	67,5	82,5	97,5	112,5
Число отказов в интервале (вес)		2	3	3	10	17	42	19	9
Накопленное число отказов		2	5	8	18	35	77	96	105
Число работоспособ-ных объектов к моменту		103	100	97	87	70	28	9	0
Частость		0,019	0,0286	0,0286	0,0952	0,1619	0,4	0,1809	0,0857
Вероятность наступления отказа		0,019	0,048	0,076	0,171	0,333	0,733	0,914	1,0
Вероятность безотказной работы		0,981	0,952	0,924	0,829	0,667	0,267	0,086	0,0
Плотность вероятности наступления отказа		0,0013	0,0019	0,0019	0,0063	0,0108	0,0267	0,0121	0,0057
Интенсивность отказов		0,0013	0,0019	0,0021	0,0076	0,0162	0,1	0,1407	-

Обозначим масштаб по оси абсцисс К_х и отложим на ней отрезки:

S_x(t)=K_x , x=K_xlg t

где К_x = L/(lg t_m_ах — lgt_min)=129/ (lg117 – lg6)= 129/(2,0682 – 0,7782) =129/1,29=100; L — ширина графика выбирается исходя из размера бумаги и таким образом, чтобы К_x было удобным, лучше круглым числом.

Принимаем К= 100мм.

Для выбора масштаба по оси ординат зададимся значениями F_min= 0,001 и F_m_ах (t) = 0,999 (при F (t) =0 и F (t)=1 выражение y= теряет смысл).

Тогда:

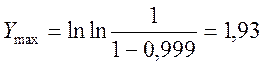
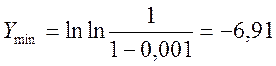
По оси ординат будем; откладывать отрезки:

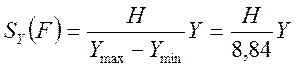
где Н - высота графика (принимаем Н= 200мм), а Y подсчитывается по формуле из табл. 8.2.

Таблица 8.2

Определяемый параметр	Номера интервалов наработки
Определяемый параметр	1	2	3	4	5	6	7	8
	7,5	22,5	37,5	52,5	67,5	82,5	97,5	112,5
x_i=lgt_i	0,8751	1,3522	1,5740	1,7202	1,8293	1,9165	1,9890	2,0512
S_x(t_i)=K_xx_{i, мм}	87,51	135,22	157,40	172,02	182,93	191,65	198,90	205,12
	0,019	0,048	0,076	0,171	0,333	0,733	0,914	1,0
1 - F(t_i)=Р(t_i)	0,981	0,952	0,924	0,829	0,667	0,267	0,086	0,0
1/[1 - F(t_i)]	1,0193	1,0504	1.0822	1,2062	1,4992	3,7453	11.628	∞
ln0,01981/[1 - F(t_i)]	0,0198	0,0488	0,0770	0,1823	0,4055	1,3191	2,4508	-
Y= lnln1/[1 - F(t_i)]	-3,922	3,0201	-2,564	-1,704	-0,904	0,2776	0,8920	-
S_Y(F_(t))=Y·200/8,84	-88,73	-68,32	-58,0	-38,54	-20,45	6,28	20,17	-

1 2 3 4 5 6 7 8

Скачать файл