Устойчивость систем автоматического регулирования

Лекция 7

(4 часа)

УСТОЙЧИВОСТЬ САР

Понятие устойчивости

Для того, чтобы замкнутая САР была работоспособной, она должна быть устойчивой.

Устойчивой является САР, реакция которой на ограниченное воздействие является также ограниченной величиной. Математически это означает, что реакция САР (рис.7.1) на воздействие  (при  для всех , где M – конечное число) описывается выражением

,

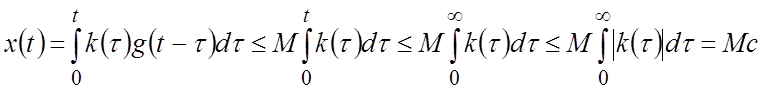где 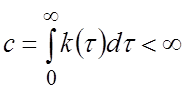 – конечное число.

Учитывая связь весовой и передаточных функций, можно утверждать, что для того, чтобы САР была устойчивой, импульсная переходная характеристика должна быть абсолютно интегрируемой. Другими словами, если абсолютная площадь, ограниченная импульсной характеристикой w(t), является ограниченной величиной, то САР будет устойчивой.

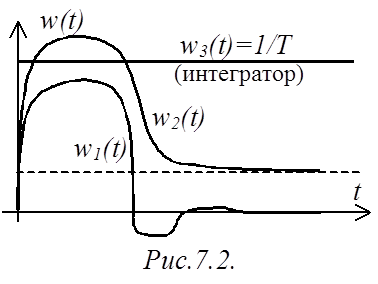Например (рис.7.2), САР с импульсной переходной характеристикой w₁(t) является устойчивой, поскольку при  w₁(t), и площадь, ограниченная импульсной характеристикой w₁(t), является ограниченной величиной (интеграл конечный). САР с импульсной характеристикой w₂(t) является неустойчивой, поскольку при  w₂(t), и интеграл является бесконечным.

В этом плане интегратор как элемент устойчивым назвать нельзя: его импульсная характеристика w₃(t) ограничивает бесконечно большую площадь (рис.7.2). Поэтому часто интегратор называют нейтральным звеном.

Площадь, ограниченная импульсной характеристикой, будет конечной, если 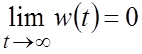. В этом случае система будет приходить в состояние равновесия ().

На основании изложенного можно считать, что устойчивой является та система, которая, будучи выведенной из состояния равновесия, возвращается в исходное состояние после исчезновения воздействия, выведшего систему из состояния равновесия.

Для определения условия, при котором 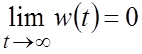 найдем выражение для w(t), учитывая связь между весовой функцией и ПФ, используя теорему разложения и считая, что все полюсы ПФ простые, причем нулевые полюсы отсутствуют. Тогда

          ,

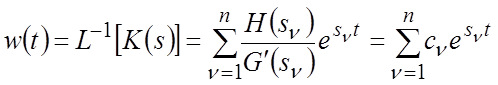где  – порядковые номера полюсов ПФ .

В общем случае полюсы – комплексные числа:

          .

Тогда

                    ,

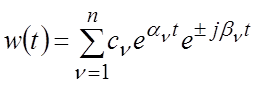где  – ограниченная величина.

Теперь из последнего выражения видно, что 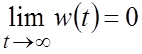, т.е. САР будет устойчивой, если вещественные части  всех полюсов будут отрицательными ().

Если же хотя бы один корень (пусть i-й) имеет положительную вещественную часть (), то САР будет неустойчивой, поскольку 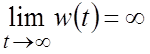 – в системе будет иметь место расходящийся процесс.

Если хотя бы один корень расположен на мнимой оси (), то САР будет неустойчивой, поскольку 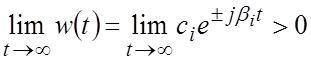, и в системе будут иметь место незатухающие автоколебания.

Геометрическая трактовка. Полюсы ПФ замкнутой системы можно изобразить на комплексной плоскости.

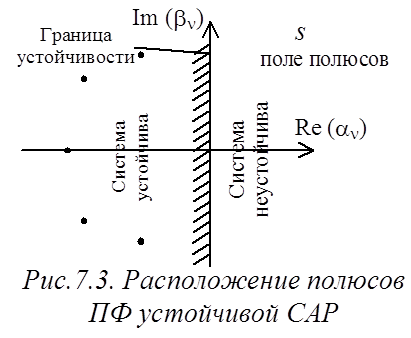Для того, чтобы САР была устойчивой, необходимо и достаточно, чтобы все полюсы ПФ замкнутой системы находились в левой полуплоскости комплексного переменного  (рис.7.3).

Наличие хотя бы одного полюса в правой полуплоскости – система неустойчива.

Если хотя бы один полюс находится на мнимой оси, то система находится на границе устойчивости. Граница устойчивости обозначается штриховкой в сторону области устойчивости.

Для сложных САР вычисление полюсов для установления их устойчивости или неустойчивости может представлять весьма сложную задачу. Поэтому известно большое количество так называемых критериев устойчивости, основанных на использовании определенных математических закономерностей при исследовании САР на устойчивость. Различают алгебраические и частотные критерии устойчивости.

Алгебраические критерии устойчивости

Основаны на выявлении требуемых алгебраических соотношений между коэффициентами характеристического полинома, гарантирующих отсутствие его правых корней. К алгебраическим относятся критерии Гурвица, Льенара-Шипара, Рауса. Наиболее распространенным является критерий Гурвица, который и рассматривается ниже.

Критерий устойчивости Гурвица (Hurwitz, 1895)

Пусть имеется характеристический полином замкнутой САР

          ,

где n – порядок САР.

Матрица Гурвица (квадратная порядка n) имеет вид:

         

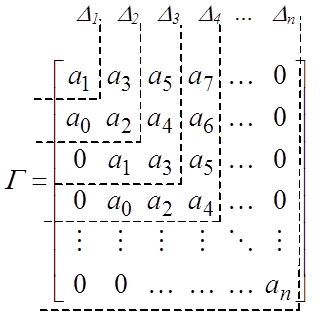
и составляется по следующему правилу:

На главной диагонали выписываются элементы , , …, . Затем при движении от этих элементов вверх записываются коэффициенты в порядке возрастания индексов, при движении вниз – в порядке убывания. Если индекс очередного записываемого коэффициента превышает n или становится отрицательным, соответствующий элемент матрицы Гурвица принимают равным нулю.

Критерий: Для того, чтобы система была устойчива, необходимо и достаточно, чтобы при  все определители Гурвица

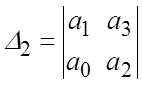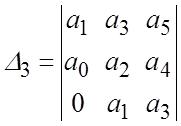          ,  ,   и т.д.

были положительны, т.е.        ,  ,  , …, .

Примечания. 1. Количество определителей равно порядку САР.

     2. Последний определитель .

     3. Если , то предварительно необходимо  умножить на –1.

Случай 1.  n=1

                   

Определитель Гурвица  .

По критерию Гурвица: ,  – система устойчива.

Тогда полюс ПФ  будет отрицательным.

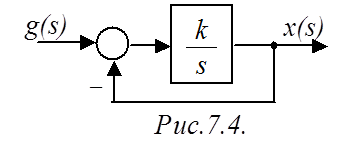Пример 1. Определить условия устойчивости САР (рис.7.4) по критерию Гурвица.

ПФ замкнутой САР

.

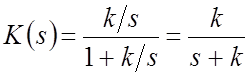Характеристический полином:      .

Условие устойчивости        .

Т.е. данная САР будет устойчива при любом положительном , даже при .

Случай 2.  n=2

                   

Определители Гурвица: , .

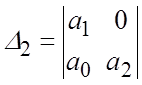По критерию Гурвица: , ,  (или ) – система устойчива.

Таким образом, для САР 1-го и 2-го порядков необходимым и достаточным условием устойчивости является положительность всех коэффициентов .

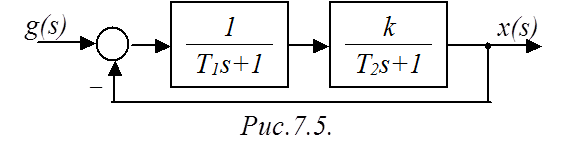Пример 2. Определить условия устойчивости САР (рис.7.5) по критерию Гурвица

ПФ замкнутой САР

.

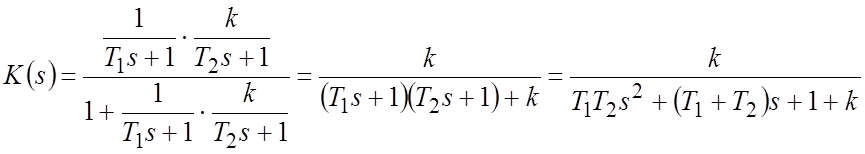Характеристический полином:            .

Случай 3.  n=3

                   

Определители Гурвица: , , .

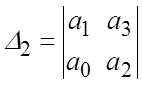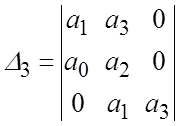По критерию Гурвица: , , , .

Рассматривая эти условия в совокупности, можно получить:

          , , , , .

Таким образом, для устойчивой САР 3-го порядка необходимо и достаточно, чтобы все коэффициенты характеристического полинома  были положительны и произведение средних коэффициентов было больше произведения крайних.

Примечание (Следствия из критерия Гурвица). Можно показать, что для системы любого порядка положительность коэффициентов характеристического полинома является необходимым, но не достаточным условием устойчивости. Пропуск хотя бы одного члена полинома (равенство соответствующего коэффициента нулю) говорит о том, что САР неустойчива.

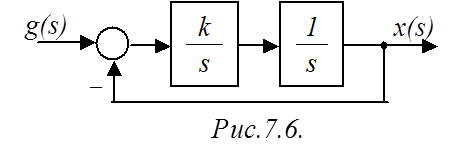Пример 3. Определить условия устойчивости САР (рис.7.6) по критерию Гурвица.

ПФ замкнутой САР

.

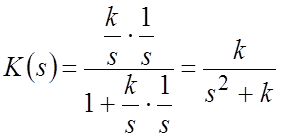Характеристический полином:      .

Уже сейчас можно утверждать, что САР будет неустойчивой, поскольку отсутствует член с .

Действительно, определители Гурвица в этом случае равны нулю и критерий не выполняется.