Частотные характеристики динамических звеньев: Методические указания по выполнению лабораторной работы

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

частотные характеристики

динамических звеньев

Методические указания

по выполнению лабораторной работы

для студентов специальности 120100

всех форм обучения

Одобрено

                          редакционно-издательским советом

                Балаковского института  техники,

              технологии и управления

Балаково  2008

Цель работы

Изучить и освоить навыки построения и анализа частотных характеристик типовых динамических звеньев.

Частотные  характеристики

Частотная характеристика является динамической характеристикой элемента системы управления. Она описывает прохождение гармонических сигналов через динамическое звено.   

Подадим  на  вход  линейного элемента  синусоидальный  сигнал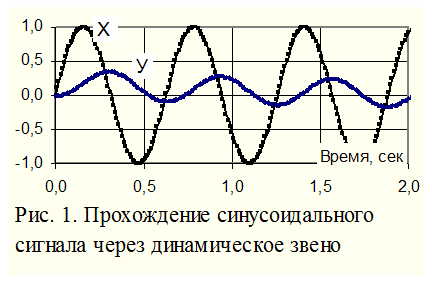     

              .

После окончания переходного процесса на  выходе  получим  сигнал  той  же  частоты,  но  другой  амплитуды  и  сдвинутый  по  фазе  на  угол  j (рис. 1):                                                                  

      .

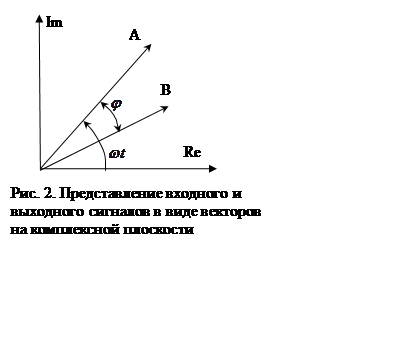
Рассмотрим представление гармонических сигналов на комплексной плоскости. Вектор А, вращающийся вокруг начала координат на комплексной плоскости со скоростью может быть представлен комплексным выражением   (рис. 2). На основании уравнения Эйлера                             

его можно разложить на две составляющие  .

Отсюда косинусоидальный и синусоидальный сигналы можно представить в виде вещественной и мнимой частей вращающегося на комплексной плоскости вектора, длина которого равна амплитуде сигнала , а скорость вращения равна круговой частоте гармонических сигналов  . Отличие синусоидального и косинусоидального сигналов заключается в отставании  фазы  относительно  на , который определяется множителем . 

Тогда выходной сигнал может быть представлен вращающимся с той же скоростью вектором,  имеющим амплитуду   и сдвинутым по отношению к вектору А по фазе  на угол  j      (см. рис.2).

Будем подавать на вход элемента синусоидальные сигналы x(t) с постоянной  амплитудой   А  и разными частотами  . Для  каждой  частоты  мы  получим  свое  значение амплитуды и фазы выходного сигнала В  и  j.

 Отношение  выходного сигнала к входному сигналу   в  комплексной  форме  называется амплитудно - фазовой частотной характеристикой АФЧХ  исследуемого элемента . Она  показывает зависимость коэффициента передачи элемента  (отношение амплитуд выходного сигнала к входному) и разности фаз между ними от частоты входного сигнала

                                             .

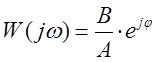Зависимость коэффициента передачи элемента от частоты называется амплитудной частотной характеристикой  АЧХ    .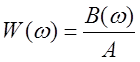

Зависимость фазы между выходным и входным сигналом от частоты называется фазо-частотной характеристикой элемента   ФЧХ    

                                    .

АФЧХ  может быть получена   из  передаточной  функции  заменой  p на jw 

                   .

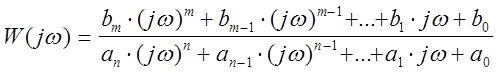Геометрически АФЧХ изображается на комплексной плоскости в полярных координатах  и представляет собой годограф, показывающий зависимость коэффициента передачи и сдвига фазы от частоты входного сигнала.

Годограф АФЧХ может быть построен и в декартовых координатах, для чего вводятся вещественная  и мнимая    частотные характеристики.

Подставим в передаточную функцию  и запишем АФЧХ в виде отношения полиномов

                      .

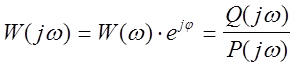Разложим числитель и знаменатель на вещественные и мнимые составляющие                                              

                                       .

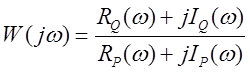Для устранения мнимой части в знаменателе умножим числитель и знаменатель на величину, сопряженную знаменателю

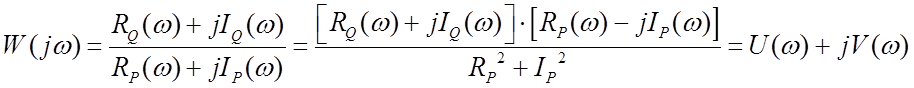
Таким  образом,  АФЧХ мы представили в виде суммы двух составляющих вещественной и мнимой частотных характеристик                          

                                     .

Из  них могут быть получены амплитудная и фазовая частотные характеристики элемента 

                ,       .

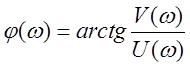         В  теории  управления  широко используются логарифмические амплитудная и фазовая характеристики.  Амплитудная фазовая частотная характеристика может быть записана   в следующих видах                     

                              .

Прологарифмируем  АФЧХ  

           .

Мы получили  комплексное  число,  вещественная  часть  которого  показывает зависимость логарифма  модуля от частоты,  а  мнимая  часть – фазы от частоты.

Десятичный логарифм амплитудной частотной характеристики  называется логарифмической амплитудной характеристикой  .

Десятичный логарифм отношения амплитуд выражается в белах. Десятичный логарифм от 10  является одним белом. Обычно анализируется отношение мощностей.  При отношении сигналов 10, мощность увеличивается  в   раз или на 2 бела. Эта единица измерения большая и в практике используют децибелы:  1 бел = 10 децибел, 2 бел = 20 децибел. Поэтому логарифмическая частотная характеристика определяется выражением

                     .  

Основным  достоинством  логарифмических  характеристик является   возможность  их построения  практически  без  расчетов  по  виду  передаточной  функции.

При  ручном  построении логарифмические характеристики удобно строить на  миллиметровой  бумаге.  По оси   абсцисс  откладывается  угловая  частота  в  логарифмическом  масштабе (удобно использовать масштаб логарифмической линейки). Диапазон частот характеристики является относительным, т.к. определяется рабочим диапазоном исследуемой системы, например,

                  

и не включает , т.к   (не существует).

  Нуль оси  ординат  может  проходить  через  ось  абсцисс при любом значении круговой частоты ,  определяемом рабочим  диапазоном  частот. Практически  ось  ординат  проводят  несколько  левее  самой  нижней сопрягающей  частоты.

На компьютере в математических пакетах для построения логарифмических частотных характеристик используются команды работы с комплексными числами.

Частотные  характеристики типовых звеньев

1. Усилительное звено

К усилительным звеньям относятся элементы, производящие мгновенное преобразование входного сигнала в выходной без переходных процессов. К безынерционным звеньям относятся электронные усилители, механические жесткие рычажные системы и т.д.

Передаточная функция безынерционного звена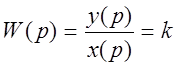                  

Частотные  характеристики:     АФЧХ,  ВЧХ,  МЧХ,  АЧХ, ФЧХ:

  ,   , ,     , 

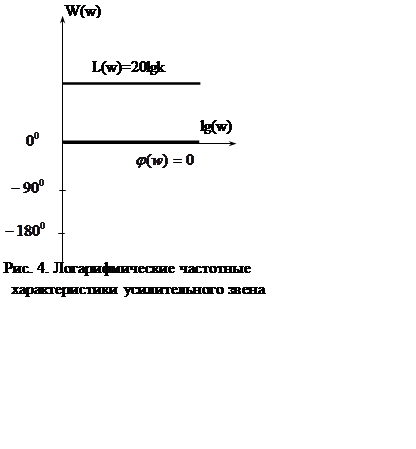
Амплитудно-фазовая частотная характеристика приведена на рис.  3.

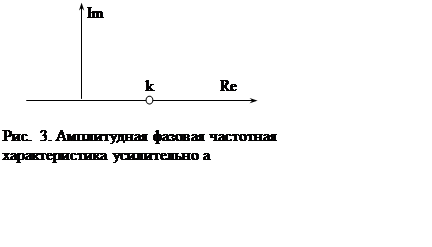
Логарифмические частотные   характеристики  (рис. 4) определяются выражениями                       .

Амплитудная характеристика для  всех частот равна , сдвиг по фазе у  данного звена отсутствует.

2. Апериодическое звено первого порядка

Передаточная функция   .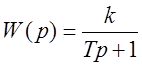 

Частотные  характеристики. Для получения частотной характеристики сделаем замену в передаточной функции , умножим полученное выражение на сопряженный знаменателю сомножитель, разделим полученную частотную характеристику на реальную и мнимую составляющие

                .

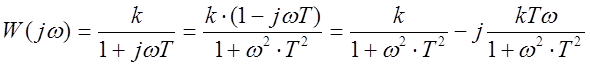Вещественная частотная характеристика  .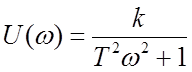

Мнимая частотная характеристика .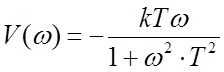

Фазовая частотная характеристика   .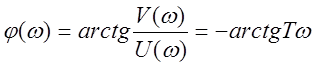

Амплитудная частотная характеристика  

                             .

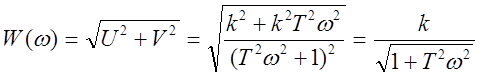Получим  аналитическое выражение  АФХ.

Проведем анализ суммы  .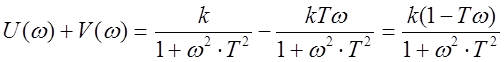

Возведем  левую  и  правую  части  в  квадрат:

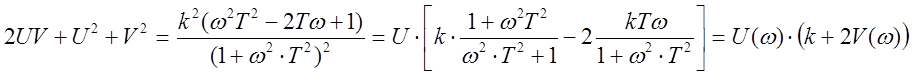
Или         .

Тогда   добавим в обе части ,  получим     

                                         .

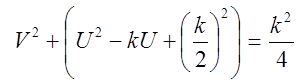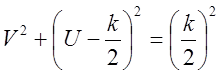  -   уравнение  окружности с центром  в  точке  (0; k/2).