Электронный регулятор напряжения синхронного генератора

Балаковский институт техники, технологии и управления

Факультет инженерно-строительный

Кафедра Управление и информатика в технических системах

курсовая работа

по дисциплине

теория автоматического управления

ЭЛЕКТРОННЫЙ  РЕГУЛЯТОР НАПРЯЖЕНИЯ СИНХРОННОГО  ГЕНЕРАТОРА

Выполнил:

 студент группы УИТ -41

Баусов Р.Ю.

Проверила:

Мартынова И.В.

Балаково 2005.

ЭЛЕКТРОННЫЙ  РЕГУЛЯТОР НАПРЯЖЕНИЯ СИНХРОННОГО  ГЕНЕРАТОРА

Электронный регулятор напряжения (ЭРН) предназначен для регулирования напряжения синхронных генераторов большой мощности в условиях изменяющейся электрической нагрузки.

Функциональная схема ЭРН приведена на рис.1, она вклю­чает объект регулирования — синхронный генератор большой мощ­ности (СГ), подключенный к нагрузке; измерительный элемент с RС-четырехполюсником (ИЭЧ), представляющий собой при номи­нальном напряжении Ucr уравновешенный мост; корректирующий элемент гибкой обратной связи (ЭГОС); фазочувствительный усили­тель (ФЧУ), преобразующий сигнал разбаланса моста в соответствую­щий сдвиг фаз управляющего напряжения тиристоров тиристорного усилителя {ТУ). Электромашинный возбудитель СГ с обмоткой возбуждения служит исполнительным элементом регулятора.

Электронный регулятор напряжения является автоматической системой статического регулирования, т. е. при изменении нагрузки

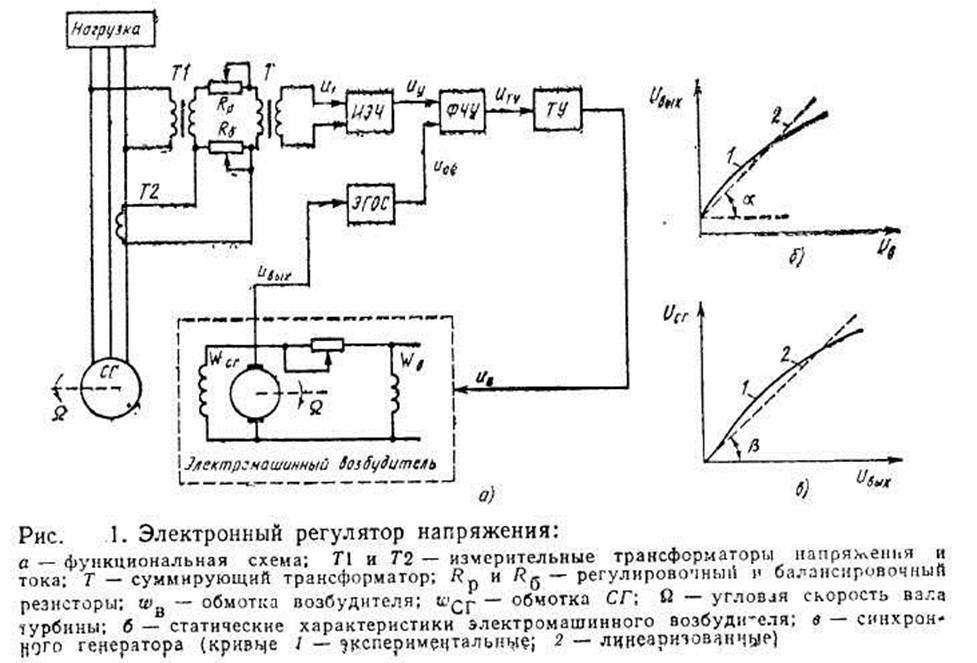
на СГ для поддержания напряжения на номинальном уровне необ­ходимо устанавливать различные токи возбуждения.

Принцип работы, уравнения и статические характеристики эле­ментов ЭРН. Для получения требуемой характеристики компаунди­рования в ЭРН применяют трансформаторы тока и напряжения, ко­торые формируют напряжение на входе ИЭЧ. Отклонение напряже­ния СГ от номинала вызывает изменение U₁ на выходе суммирующего трансформатора, т. е.

где k_т — коэффициент трансформации; U_cг — напряжение синхрон­ного генератора.

Напряжение на выходе измерительного моста

где k_им — передаточный коэффициент моста.

Сигнал u_им(t) поступает на четырехполюсник, состоящий из ре­зистора R и емкости С. Дифференциальное уравнение четырехпо­люсника

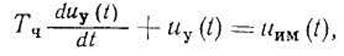
где U_y(t) — напряжение, поступающее на вход ФЧУ; Тч = RC — постоянная времени четырехполюсника.

Напряжение на базе входного транзистора ФЧУ равно разности напряжений:

где u_ос(t) — сигнал обратной связи элемента гибкой ОС.

Напряжение на выходе ФЧУ (на входе тиристорного усилителя)

Из рассмотренных выше уравнений получим сле­дующие передаточные функции:

Передаточная функция ТУ регулятора

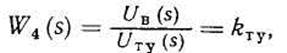
где u_в(t) — напряжение на входе возбудителя; k_ту— коэффициент передачи ТУ.

С выхода оконечного каскада усилителя напряжение поступает на обмотку  возбудителя, затем на якорь генератора постоянного тока и обмотку возбуждения синхронного генератора . Дифферен­циальное уравнение обмотки  возбудителя и якоря генератора, питающего обмотку возбуждения СГ, имеет вид

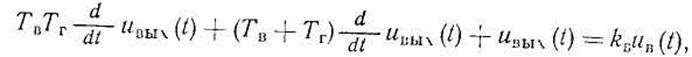
где u_вых(t) — напряжение на выходе электромашинного возбудителя; Тв — постоянная времени обмотки возбуждения генератора по­стоянного тока; Тг — постоянная времени обмотки возбуждения СГ; к_в — передаточный коэффициент возбудителя.

Дифференциальное уравнение синхронного генератора

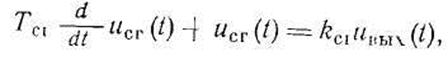
где k_сг— передаточный коэффициент СГ; Тсг— постоянная времени. Экспериментальные статические характеристики электромашин­ного возбудителя и СГ приведены. Соответствующие коэффициенты передачи определяют по линеаризованным характе­ристикам. k_в = tg; k_сг = tg .

Дифференциальное   уравнение   корректирующего   элемента — гибкой ОС

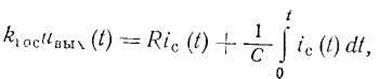
где k_гос — коэффициент гибкой обратной связи; i_c(t) — ток коррек­тирующего элемента.

В соответствии с уравнениями получим передаточные функции:

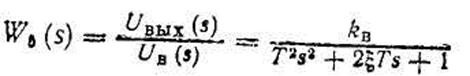
электромашинного    возбудителя

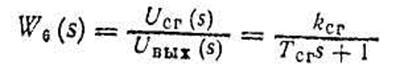
— объекта регулирования — синхронного генератора;

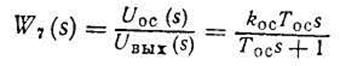
— элемента гибкой ОС (здесь Тос — постоянная времени).

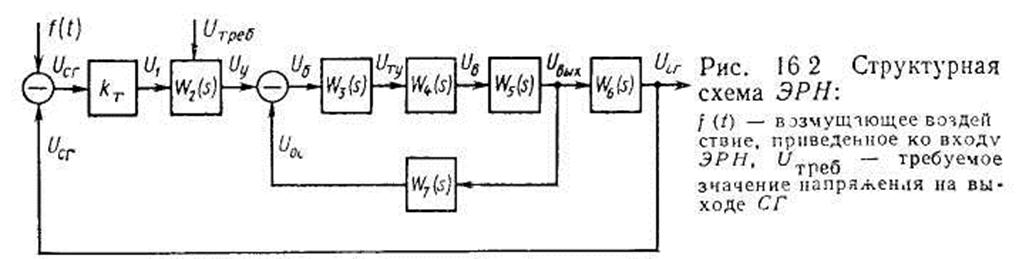
Структурная схема ЭРН, составленная в соответствии с переда­точными функциями W₁(s) —W7 (s) и уравнением сравнивающего элемента фазочувствительного транзисторного усилителя:

Передаточная функция системы с разомкнутой главной ОС

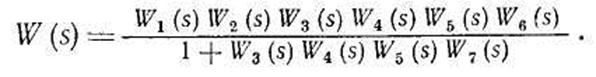
Используя выражение и выражения передаточных функ­ций элементов, получим Ф(s) — передаточную функцию электрон­ного регулятора напряжения как замкнутой САР:

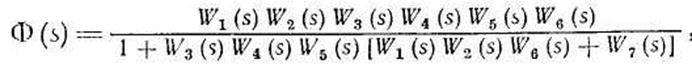
если s0, то получим статический коэффициент ЭРН

где К=к_тк_чк_иэк_фчук_тук_вк_сг, который характеризует статизм регу­лирования напряжения.

  Анализ устойчивости процесса регулирования напряжения СГ, а также анализ качества поддержания напряжения относительно но­минального значения можно выполнить в соответствии с данными выраже­ниями.

Величина статизма регулирования в системе может изменяться с помощью схемы токовой стабилизации, состоящей из резисторов, включенных в цепь трансформатора тока. Таким образом обеспечи­вается устойчивое распределение реактивной нагрузки между парал­лельно работающими генераторами.

Для синхронных генераторов, работающих на дальние линии электропередачи, закон регулирования усложняется за счет введе­ния воздействия по отклонению напряжения и его производных по времени, а также по току статора и его производным.

Проверим систему  на устойчивость, по критерию устойчивости Ляпунова.

Найдем полюса (корни характеристического уравнения) передаточной функции   для замкнутой системы:

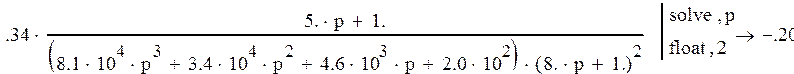
Полюс имеет отрицательную вещественную часть, следовательно, система устойчива.

    Построим переходный процесс и определим прямые оценки качества системы.

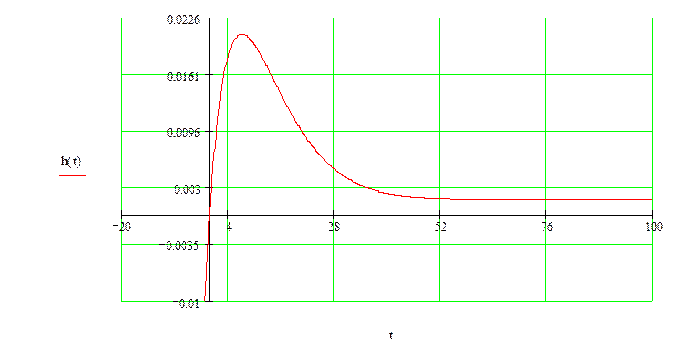
1.  Время переходного процесса системы – это время регулирования системы, определяется как интервал времени от момента приложения какого-либо воздействия на систему до времени вхождения системы в 5% трубку. tn = 7 51с

2.  Перерегулирование (максимальная динамическая ошибка)

    

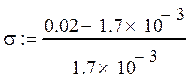
3.  Колебательность – число колебаний системы от момента воздействия на нее до перехода в установившееся состояние.  N=0

4.  Время нарастания регулируемой величины – время, при котором выходная величина достигает своего максимального значения.  tm=7.27с.

  5.     Время первого согласования – время, за которое регулируемая величина первый раз достигнет своего установившегося значения. t₁ = 0.098c.

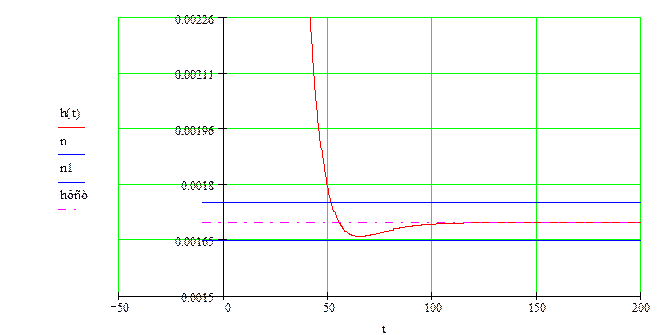
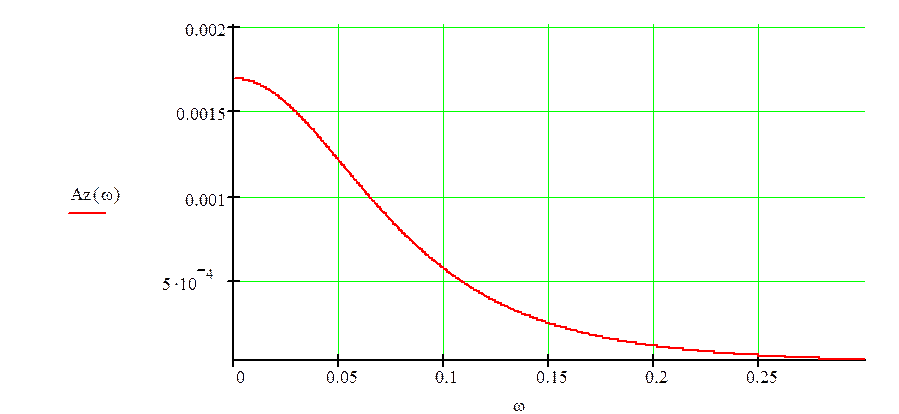
Построим  АЧХ замкнутой системы и определим косвенные оценки качества системы.

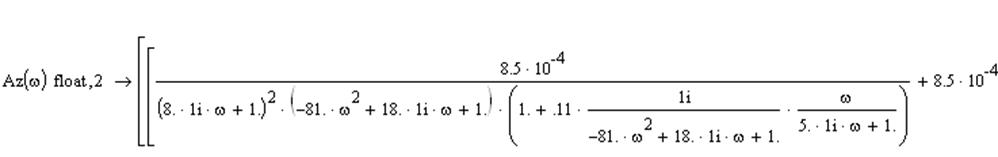
1.  Показатель колебательности: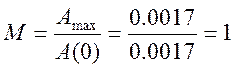

2.  Резонансная частота – частота, при которой амплитуда достигает значения максимума: wр=0

3.  Частота среза определяется как частота, при которой АЧХ принимает значение      A=1, в данной системе отсутствует.    

4.  Полоса пропускания частот – интервал частот, когда значения АЧХ не менее, чем 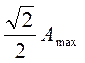 откладываем ее на АЧХ и в точках пересечения с графиком получаем частоты определяющие полосу пропускания (=1.202E-3):  (w1, w2) = (0; 0.05).

Построение ЛАЧХ И ЛФЧХ и определение запасов устойчивости

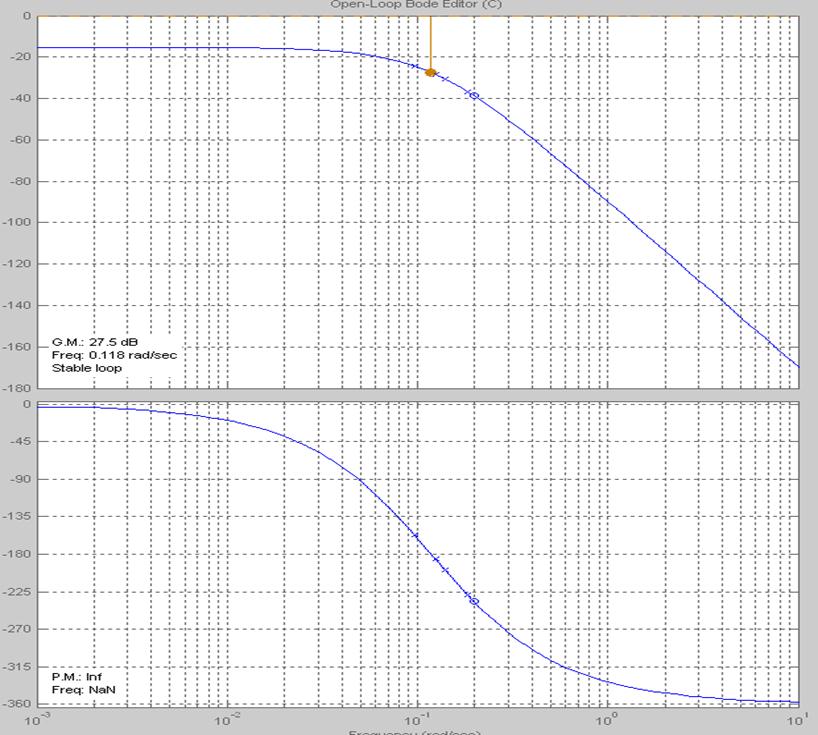
 Определяем запас по амплитуде. Из точки  проводим пря­мую вертикально вверх до пересечения с ЛАЧХ находим точку пересечения. Следовательно запас устойчивости по амплитуде будет равен А=-27.5Дб и определяется при частоте 0.118 рад/сек.

  Запас устойчивости по фазе отсутствует т.к коэффициент усиления мал.

  ВЫВОД: Анализ линейной части системы показывает, что данная ЛАХ отрицательна (т.е. расположена ниже оси абсцисс), следовательно данная САУ устойчива.

Анализ нелинейной СУ

1. Структурная схема СУ с нелинейным элементом

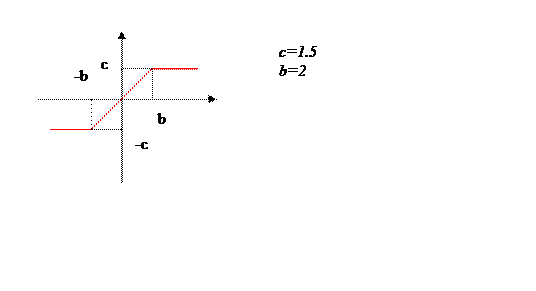
Нелинейный элемент представляет собой чувствительный элемент с идеальной статической характеристикой с зоной насыщения.

2. Преобразование структурной схемы

Размыкаем структурную схему перед нелинейным элементом, получим:

Затем преобразуем линейную часть системы:

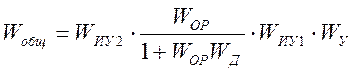
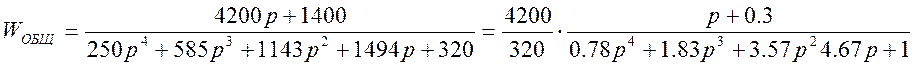
Разделим числитель и знаменатель на выражение (p+0.3):

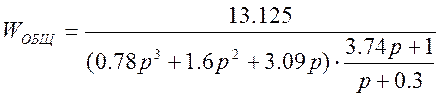
Так как наглядное представление фазовых траекторий возможно только для систем, порядок которых не выше второго, то передаточная функция будет иметь вид:

3. Построение фазового портрета

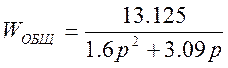
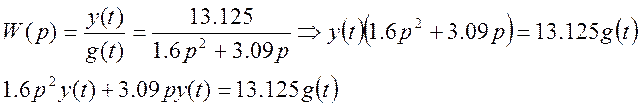
Сделаем замену:

Линейная часть системы будет описываться следующим дифференциальным уравнением:

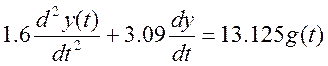
Уравнение нелинейного элемента

Уравнение сравнивающего элемента

Предположим, что задающее воздействие x(t)=0. Тогда уравнение нелинейной системы будет иметь следующий вид

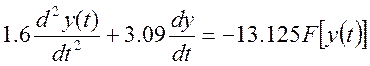
Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них составляется линейное дифференциальное уравнение

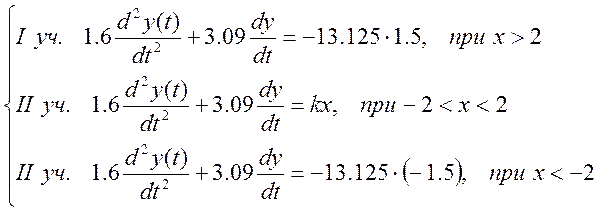
Сделаем замену:

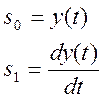
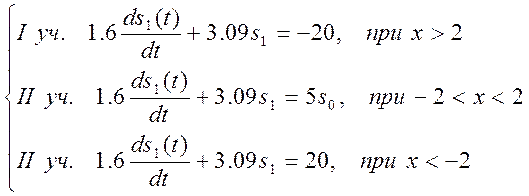
Разделим правые и левые части этих уравнений на 1,6:

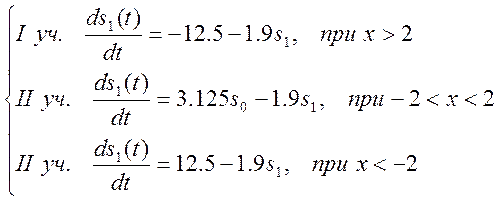
Определим функцию D по 3-м линейным участкам нелинейной статической характеристики, задающую производную, приведя дифференциальное уравнение 2-го порядка к системе 2-х дифференциальных уравнений 1-го порядка

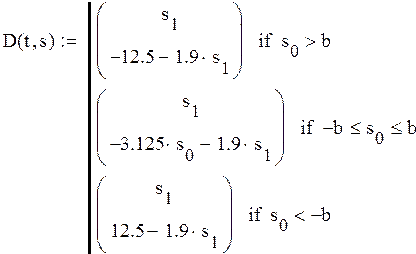
Зададим начальное значение для вектора s:

Найдем матрицу решения

Построим траекторию на фазовой плоскости, предполагая, что первый столбец матрицы решения S_i,0 содержит точки, в которых ищется решение дифференциального уравнения, второй S_i,1 – содержит значения найденного решения (первая производная), и, наконец, третий столбец S_i,2 содержит вторые производные этого решения.

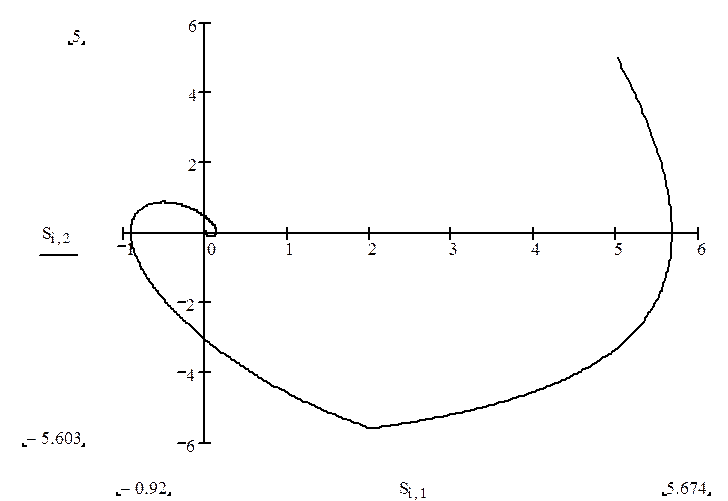
По полученному фазовому портрету построим график переходной функции.

Фазовая траектория стремится к нулевому значению, что говорит об устойчивости системы.  Вид фазовой траектории показывает, что качество управления удовлетворительное. Улучшения качества можно добиться путем замены элементов системы, или изменением параметров уже имеющихся элементов.

На фазовой плоскости изображена фазовая траектория для комплексных корней с отрицательными вещественными частями, следовательно получена особая точка «устойчивый фокус». А из графика переходной функции видно, что система устойчива.