Частотные характеристики динамических звеньев: Методические указания по выполнению лабораторной работы, страница 2

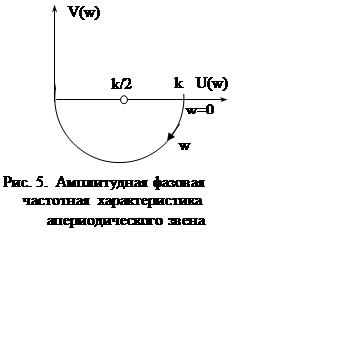
Таким  образом,  АЧХ  имеет  вид  полуокружности (рис. 5).  При  w=0  сдвиг  по  фазе  равен  нулю,  коэффициент  передачи  равен  k.  С  увеличением  частоты  модуль  уменьшается,  а  сдвиг  по  фазе  стремится  от  0  к  минус 90°

 (при  w®¥,  j®- 90°).

Логарифмические частотные характеристики ЛЧХ.

;   ;  .

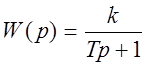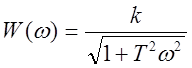Разобьем  ЛАХ  по  оси  частот  на  2  диапазона.

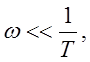
1.      -  асимптота  с  левой  стороны.

2. ,   . 

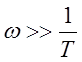Рассмотрим это выражение на численном примере.

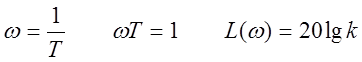
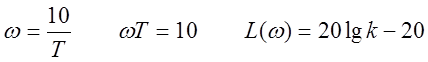
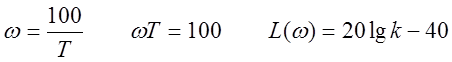
При увеличении круговой частоты  в 10 раз правое слагаемое увеличивается на 20 единиц, т.е. после частоты среза  ЛАЧ имеет наклон  20 дБ/дек.

Эти данные позволяют достаточно просто строить ЛАЧ апериодического звена первого порядка (рис. 6).

1. Построить вертикальную линию на частоте среза   .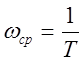

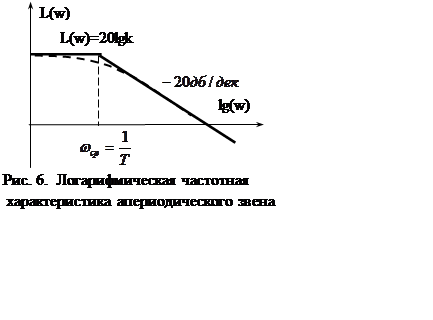2. В диапазоне нижних частот от частоты среза построить горизонтальную линию  .

3. В диапазоне высоких частот от частоты среза через точку пересечения  с вертикалью частоты среза провести ниспадающую линию с наклоном 20 дБ/дек. 

Эти две прямые линии дают амплитудную частотную характеристику звена в логарифмическом масштабе. Максимальное отклонение данной аппроксимации от расчетной кривой составляет 3дБ на частоте среза.

Логарифмическая фазовая характеристика ЛФХ строится по шаблону или расчетным путем по выражению .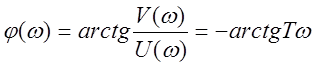

На низких частотах выходной сигнал совпадает по фазе с входным  , затем появляется отставание по фазе, которое на частоте среза равно 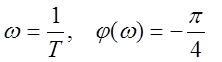. Максимальное отставание по фазе составляет .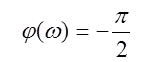

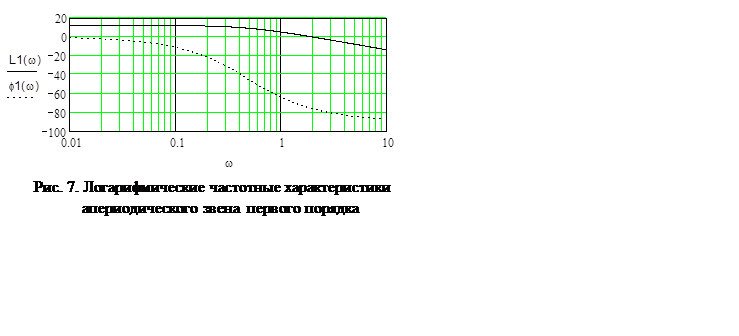
Пример построения логарифмических частотных характеристик для звена первого порядка 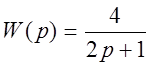  приведен на рис. 7.

3. Интегрирующее звено

Передаточная функция  интегрирующего звена   .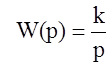

Частотные  характеристики. Произведем замену  в передаточной функции   

                                              .        

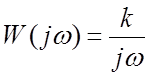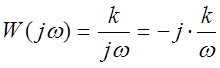Амплитудная фазовая частотная характеристика  .

Вещественная частотная характеристика  .

Мнимая частотная характеристика                            

                 .

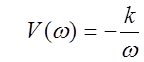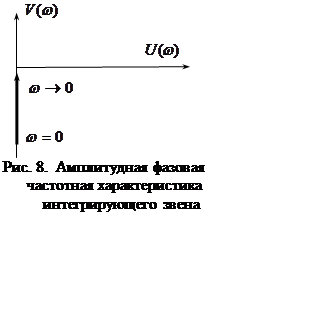
Амплитудная частотная характеристика. Найдем  модуль  частотной  характеристики (рис. 8).

                         .  

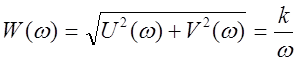Фазовая частотная характеристика   

                 .

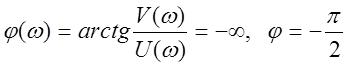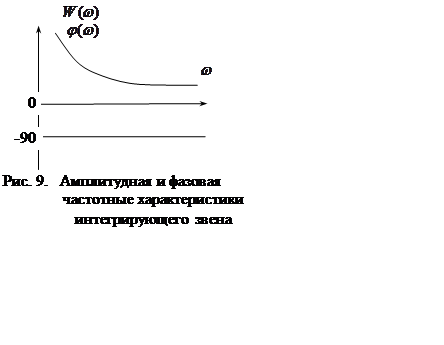Амплитудная фазовая частотная характеристика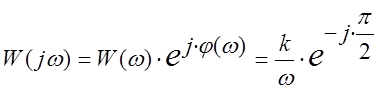

Таким  образом,  модуль  частотной  характеристики  (коэффициент  передачи)  уменьшается  с  увеличением  частоты,  а  фазовый  сдвиг  равен  =const (рис. 9).

Логарифмические частотные характеристики.

.

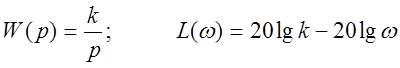Рассмотрим численный пример

,

,

.

Таким образом ЛАХ интегрирующего звена всегда имеет наклон   -20дБ/дек. Для построения ЛАХ надо провести линию с наклоном через одну точку, принадлежащую ЛАХ (рис. 10).

Метод 1.  Провести линию через точку    .

Метод 2. Выражение для ЛАХ можно записать в виде 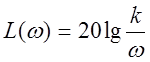 .   когда  .

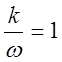Отсюда точка       также принадлежит ЛАХ данного звена. Для построения ЛАХ необходимо провести линию с наклоном -20дБ/дек через эту точку.

Метод 3. Провести линию через эти две найденные точки.

Интегрирующее звено на всех частотах  имеет отставание по фазе 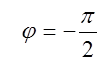 (см. рис. 10).

4. Дифференцирующее звено

1. Дифференциальное уравнение     .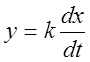  

2. Частотные  характеристики. Произведем замену  в передаточной функции      .         

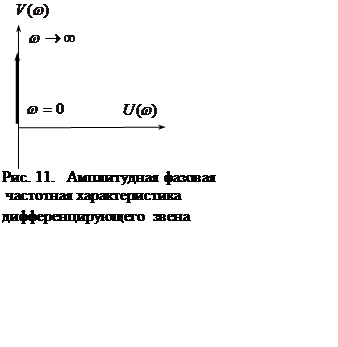
Амплитудная фазовая частотная характеристика  (см. рис. 11). 

Вещественная частотная характеристика  .

Мнимая частотная характеристика       .

Амплитудная частотная характеристика.

Найдем  модуль  частотной  характеристики.

.   

Фазовая частотная характеристика    .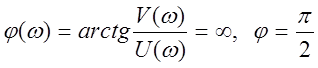

Амплитудная фазовая частотная характеристика  

            .

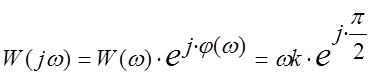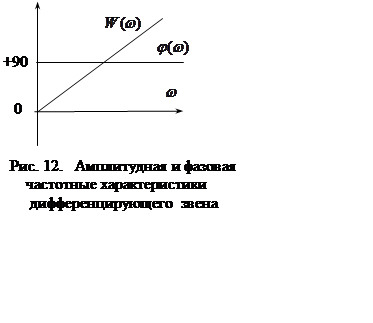
Таким  образом,  модуль  частотной  характеристики  (коэффициент  передачи)  увеличивается  с  увеличением  частоты,  а  фазовый  сдвиг  равен  =const (рис. 12).

Логарифмические частотные характеристики.

.

Рассмотрим численный пример

,

,

.

Таким образом ЛАХ интегрирующего звена всегда имеет наклон   +20дБ/дек. Для построения ЛАХ надо провести линию с наклоном через одну точку, принадлежащую ЛАХ, которой может быть точка   .

Дифференцирующее  звено на всех частотах  имеет опережение  по фазе 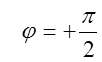     (рис. 13).

Порядок выполнения работы

1.  Включить компьютер и вызвать MathCad.

2.  Создать новый файл, дать файлу название и записать на жесткий диск. В дальнейшем в процессе работы периодически (один раз в 10-15 мин производить перезапись файла).

3.  В первой строке ввести наименование лабораторной работы,  фамилию, инициалы студента и номер группы (см. пример на с. 16-18).

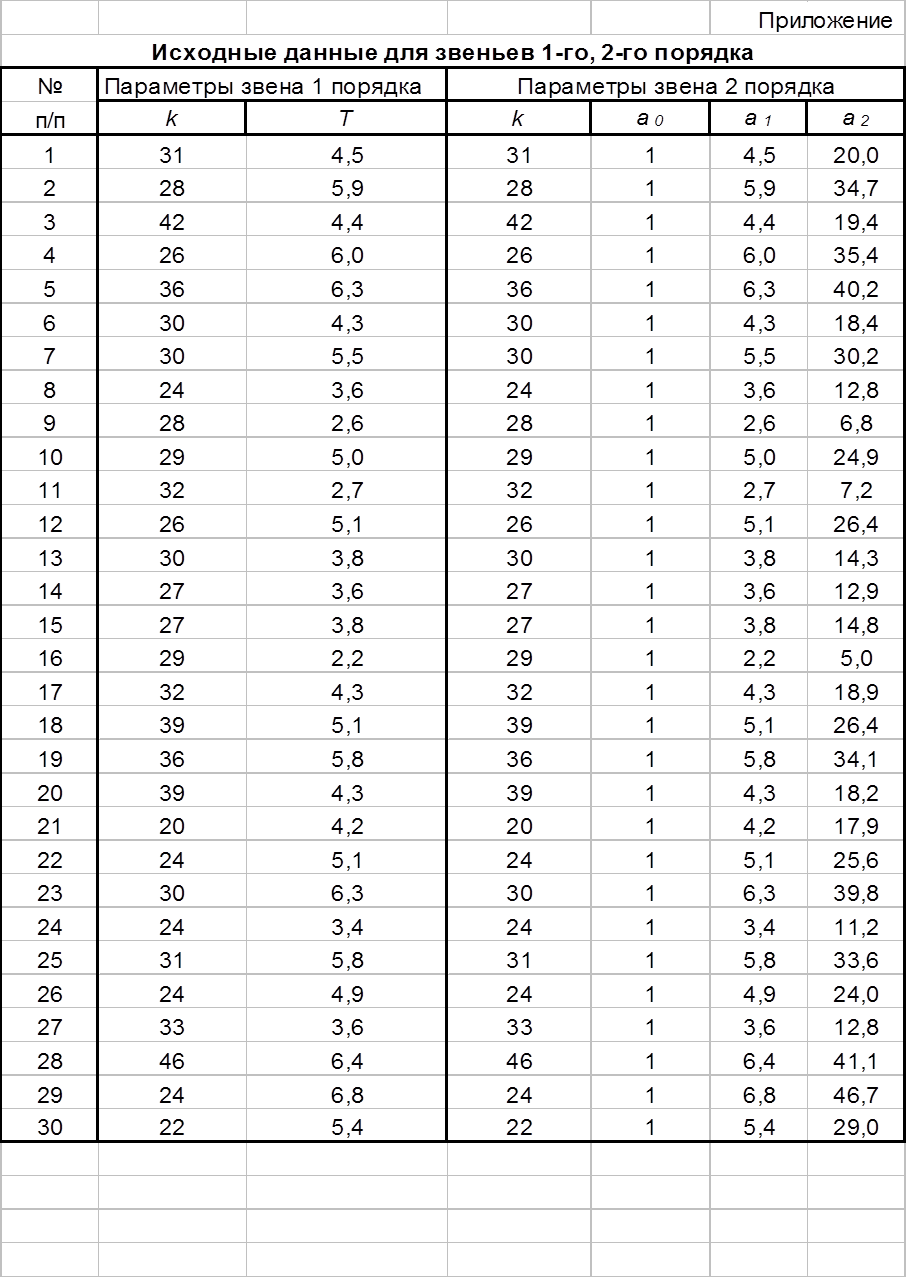
4.  Из таблицы, приведенной в приложении, ввести, согласно варианту, значения параметров элементов.

5.  Ввести передаточную функцию звена первого порядка. Ввести мнимую единицу и частотный диапазон построения частотных характеристик. Заменить в передаточной функции . Записать выражения для модуля и фазы амплитудно-частотной характеристики звена первого порядка. Построить графики амплитудной и фазовой частотных характеристик.

6.  Ввести выражение для логарифмической частотной характеристики и построить графики амплитудной и фазовой логарифмических частотных характеристик. По шкале частот поставить логарифмический масштаб.

7.  Ввести передаточную функцию звена второго порядка и аналогично построить частотные характеристики.

8.  Изменить коэффициенты звена второго порядка, чтобы получить колебательное звено, если исходное апериодическое, или апериодическое, если исходное колебательное. Построить частотные характеристики для полученного звена.

9.  Форматирование программы  и графиков. 

  a.  Установить границы страниц листа MathCad, используя команды меню Файл.

  b.  Перемещая элементы программы и графики,  изменяя размеры графиков,  добиться наглядного представления результатов и минимального количества страниц.

  c.  Используя команду «Предварительный просмотр» убедиться, что программа  и графики находятся на нужных страницах. 

  d.  Записать программу на дискету для использования при выполнении курсовой работы.

  e.  Распечатать работу на принтере.

Отчет по работе перед преподавателем

 При зачете работы студент должен:

1.  Знать закономерности получения и построения частотных характеристик динамических звеньев на основе передаточных функций, методы их расчета и построения графиков в MathCad.

2.  Понимать и  объяснять полученный вид частотных характеристик, их зависимость от параметров передаточной функции.

Список использованной литературы

1.  Клюев А.С.  Автоматическое регулирование. -М.: Энергия, 1973. – 392с.

2.  Бесекерский В.А. Теория систем автоматического регулирования.-М.: Наука,1972.–768с.

3.  Цыпкин Я.З. Основы теории автоматических систем. -М.: Наука, 1977.- 560 с.

4.  Зайцев Г.Ф. Теория автоматического управления и регулирования. -К.: Вища школа, 1975.- 424с.

5.   Куропаткин П.В. Теория автоматического управления. -М.: Высшая школа, 1973.- 528с.

6.  Юревич Е.И. Теория автоматического управления. -Л.: Энергия, 1975. – 416с.

частотные характеристики

динамических звеньев

Методические указания

по выполнению лабораторной работы

для студентов специальности 120100

всех форм обучения

Составил

Бирюков Владимир Петрович

Рецензент  О.В. ВИШТАК

Корректор А.М. Рогачева

Редактор Л.В. Максимова

Подписано в печать                                            Формат 60х84 1/16

Бум. тип.                          Усл. печ. л.1,25                       Уч.-изд.л  1,2  

               Тираж  150 экз.                     Заказ                            Бесплатно

Саратовский государственный технический университет

410054, г. Саратов, ул. Политехническая, 77

Копипринтер БИТТиУ, 413840, г. Балаково, ул. Чапаева, 140