 Положительным
считается переход частотной характеристики
Положительным
считается переход частотной характеристики ![]() через
вещественную ось левее точки с координатами (–1; j0) при
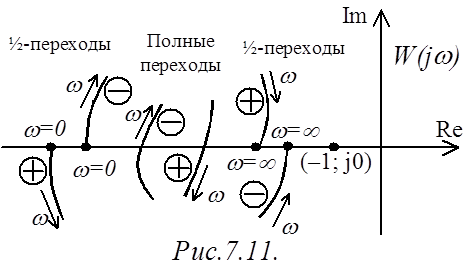
возрастании частоты w по направлению сверху вниз (рис.7.11). Отрицательным
считается аналогичный переход, но по направлению снизу вверх (рис.7.11). Если
частотная характеристика начинается или заканчивается на действительной оси
левее точки с координатами (–1; j0), то говорят о ½-переходе (рис.7.11).
через
вещественную ось левее точки с координатами (–1; j0) при
возрастании частоты w по направлению сверху вниз (рис.7.11). Отрицательным
считается аналогичный переход, но по направлению снизу вверх (рис.7.11). Если
частотная характеристика начинается или заканчивается на действительной оси
левее точки с координатами (–1; j0), то говорят о ½-переходе (рис.7.11).
Формулировка, основанная на понятии переходов. Для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов частотной характеристики левее точки с координатами (–1; j0) при изменении частоты w от нуля до +¥ была равна половине порядка неустойчивости разомкнутой САР m/2.
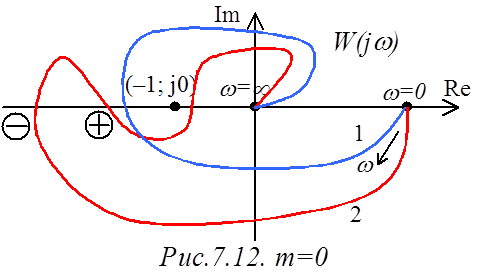 Например, замкнутая САР, имеющая в разомкнутом
состоянии частотную характеристику 1 (рис.7.12), является неустойчивой,
поскольку ЧХ охватывает точку с координатами (–1; j0) в
отрицательном направлении, а замкнутая САР, соответствующая ЧХ 2 разомкнутой
САР – устойчива, поскольку не охватывает точку с координатами (–1; j0).
Например, замкнутая САР, имеющая в разомкнутом
состоянии частотную характеристику 1 (рис.7.12), является неустойчивой,
поскольку ЧХ охватывает точку с координатами (–1; j0) в
отрицательном направлении, а замкнутая САР, соответствующая ЧХ 2 разомкнутой
САР – устойчива, поскольку не охватывает точку с координатами (–1; j0).
Устойчивость астатических систем
Пусть имеется астатическая система ![]() -го порядка с ПФ разомкнутой САР
-го порядка с ПФ разомкнутой САР
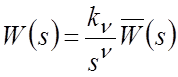 ,
,
где
![]() – нормированная ПФ разомкнутой САР.
– нормированная ПФ разомкнутой САР.
Частотная характеристика астатической САР
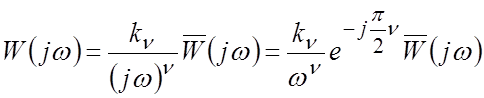
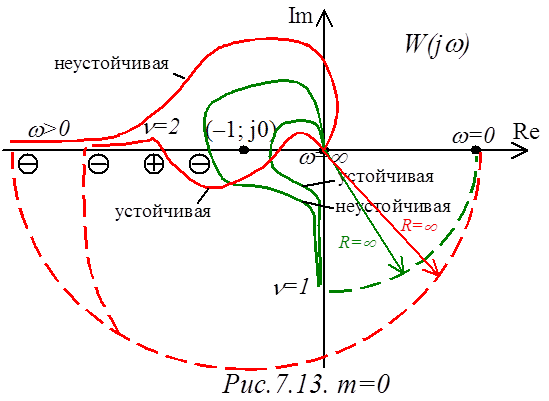 стремится к нулю при
стремится к нулю при ![]() (т.е. ЧХ
заканчивается в начале координат), а при
(т.е. ЧХ
заканчивается в начале координат), а при ![]() будет
стремиться к бесконечности при угле
будет
стремиться к бесконечности при угле ![]() (рис.7.13). Это
обстоятельство приводит к неоднозначности использования критерия Найквиста.
(рис.7.13). Это
обстоятельство приводит к неоднозначности использования критерия Найквиста.
Во избежание неопределенности частотные характеристики
дополняются дугами длиной ![]() бесконечно большого
радиуса (рис.7.13, пунктирные линии) и после этого анализируются дополненные
ЧХ:
бесконечно большого
радиуса (рис.7.13, пунктирные линии) и после этого анализируются дополненные
ЧХ:
Замкнутая САР будет устойчивой, если ЧХ разомкнутой
САР ![]() раз охватывает (или, если m=0) не охватывает точку с координатами (–1; j0) (рис.7.13).
раз охватывает (или, если m=0) не охватывает точку с координатами (–1; j0) (рис.7.13).
Применение критерия Найквиста
к логарифмическим частотным характеристикам
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) разомкнутой САР, как известно, вычисляется по формуле:
![]() ,
,
а логарифмическая фазо-частотная характеристика (ЛФЧХ) – по формуле
![]() .
.
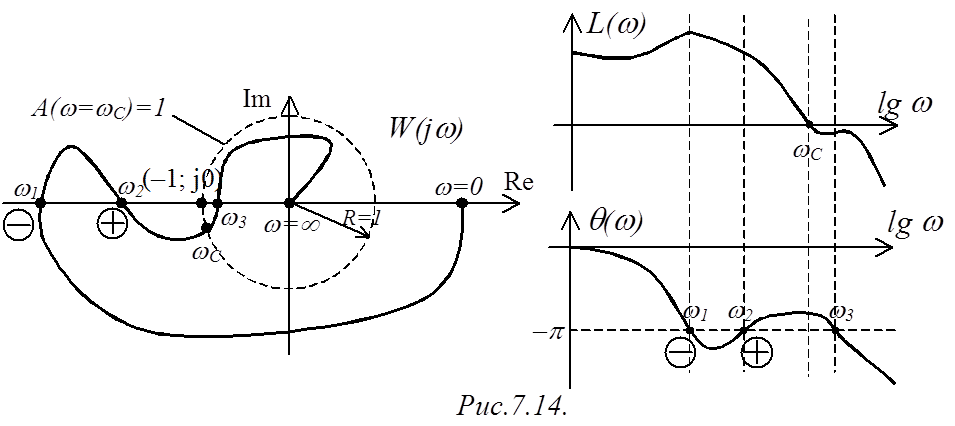
Из ЧХ (рис.7.14) следует, что достижению частотной
характеристикой окружности радиуса 1 с центром в начале координат при
определенной частоте wС,
называемой частотой среза или граничной частотой, соответствует
пересечение ЛАЧХ ![]() оси частот (
оси частот (![]() ).
).
Переходу годографа через вещественную ось при ![]() соответствует переход ЛФЧХ
соответствует переход ЛФЧХ ![]() через отметку
через отметку ![]() (В более сложных случаях, когда ЧХ
имеет вид спирали – через отметки
(В более сложных случаях, когда ЧХ
имеет вид спирали – через отметки ![]() ,
, ![]() ,
, ![]() ,
…). При этом положительному переходу соответствует переход ЛФЧХ снизу
вверх, а отрицательному переходу – сверху вниз.
,
…). При этом положительному переходу соответствует переход ЛФЧХ снизу
вверх, а отрицательному переходу – сверху вниз.
Поэтому на основании критерия Найквиста может быть сформулирован:
Логарифмический частотный критерий устойчивости.
Для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между
числом положительных и отрицательных переходов ЛФЧХ разомкнутой САР через линию
![]() (где k
= 0, 1, 2, …) при частотах, когда
(где k
= 0, 1, 2, …) при частотах, когда ![]() , была равна
, была равна ![]() .
.
Запас устойчивости
Вид частотной характеристики ![]() ,
как мы знаем, зависит от параметров разомкнутой САР. Путем изменения параметров
САР (например, изображенной на рис.7.14) можно из области устойчивости
перевести ее в область неустойчивости, и наоборот. Количественные параметры
(т.е. степень) изменения параметров устойчивой (функционирующей) САР,
необходимые для перевода ее на границу устойчивости (когда ЧХ проходит через
точку с координатами (–1; j0)) характеризуют запас
устойчивости САР.
,
как мы знаем, зависит от параметров разомкнутой САР. Путем изменения параметров
САР (например, изображенной на рис.7.14) можно из области устойчивости
перевести ее в область неустойчивости, и наоборот. Количественные параметры
(т.е. степень) изменения параметров устойчивой (функционирующей) САР,
необходимые для перевода ее на границу устойчивости (когда ЧХ проходит через
точку с координатами (–1; j0)) характеризуют запас
устойчивости САР.
Наиболее удобно количественное выражение запаса устойчивости может быть определено с помощью логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ), причем различают запас устойчивости по амплитуде (определяемый по ЛАЧХ) и запас устойчивости по фазе (определяемый по ЛФЧХ).
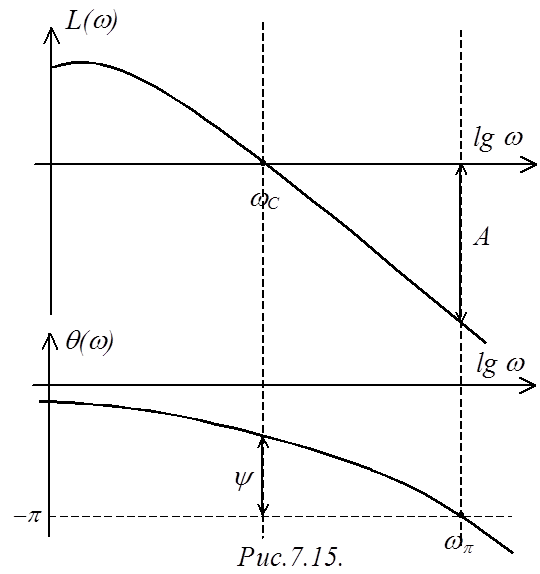 Пусть имеется
разомкнутая САР, логарифмические частотные характеристики которой приведены на
рис.7.15.
Пусть имеется
разомкнутая САР, логарифмические частотные характеристики которой приведены на
рис.7.15.
Параметр A называется запасом устойчивости по амплитуде, определяется как отклонение ЛАЧХ от оси частот при частоте, соответствующей первому отрицательному переходу ЛФЧХ через уровень –p:
![]() .
.
Предположим, что путем изменения параметров САР (путем увеличения коэффициента передачи) ее ЛАЧХ поднялась на величину A, и пусть при этом ЛФЧХ осталась без изменения. В этом случае САР находится на границе устойчивости.
Параметр y называется запасом устойчивости по фазе, определяется как отклонение ЛФЧХ от уровня –p при значении частоты w, равном частоте среза wС:
![]() .
.
Предположим, что также путем изменения параметров САР (путем установки фильтра с коэффициентом передачи, равном 1) ее ЛФЧХ опустилась на угол y, а ЛАЧХ осталась без изменения. И теперь САР находится на границе устойчивости.
В реальных САР в процессе работы под действием внешних факторов их параметры изменяются. При этом изменяются их ЛАЧХ и ЛФЧХ.
Для того, чтобы обеспечить нормальную (устойчивую) работу САР, обычно необходимо обеспечить запас устойчивости по амплитуде
![]() дБ
дБ
и запас устойчивости по фазе
![]() .
.
При невыполнении этих условий в процессе работы системы имеется большая вероятность того, что она окажется неустойчивой.
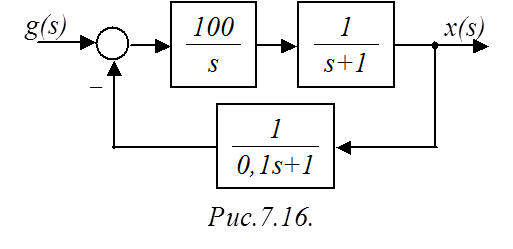 Пример 1.
Исследовать на устойчивость САР, структурная схема которой представлена на
рис.7.16.
Пример 1.
Исследовать на устойчивость САР, структурная схема которой представлена на
рис.7.16.
Решение с помощью критерия устойчивости Гурвица.
ПФ разомкнутой САР:
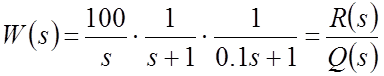 .
.
Характеристический полином замкнутой САР:
![]() ,
,
т.е. ![]() 0,1
0,1![]() ,
, ![]() 1,1,
1,1,
![]() ,
, ![]() .
.
Составляем матрицу Гурвица:
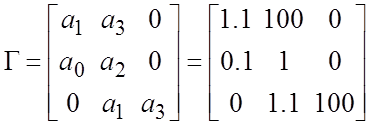 .
.
Находим определители:
![]() ;
; ![]() – САР неустойчива.
– САР неустойчива.
Решение с помощью логарифмического частотного критерия.
Строим ЛАЧХ и ЛФЧХ разомкнутой САР (рис.7.17). Имеем
один отрицательный переход ЛФЧХ через уровень –p, а положительные переходы отсутствуют,
т.е. разность между числом положительных и отрицательных переходов равна –1.
Характеристический полином разомкнутой САР ![]() не
имеет правых корней. Таким образом, логарифмический критерий не выполняется: 0 ¹ –1.
не
имеет правых корней. Таким образом, логарифмический критерий не выполняется: 0 ¹ –1.
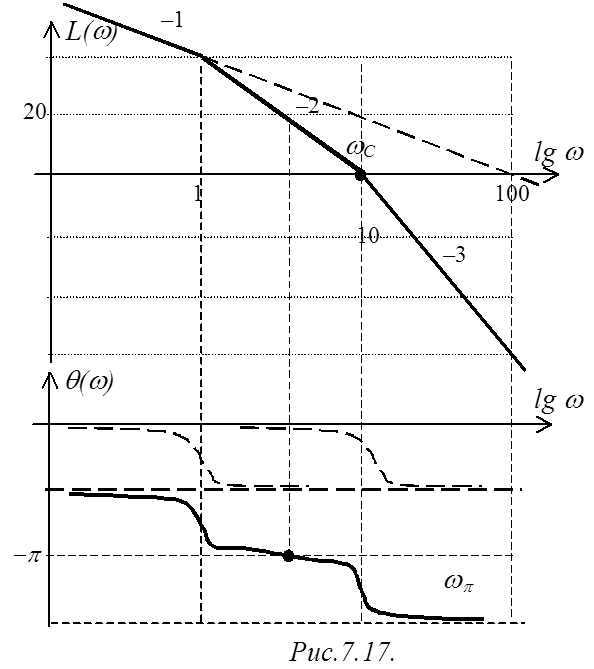 Кроме того, из ЛАЧХ и
ЛФЧХ также видно, что САР имеет отрицательный запас устойчивости как по амплитуде,
так и по фазе. Уже по этому мог бы быть сделан вывод о неустойчивости замкнутой
САР.
Кроме того, из ЛАЧХ и
ЛФЧХ также видно, что САР имеет отрицательный запас устойчивости как по амплитуде,
так и по фазе. Уже по этому мог бы быть сделан вывод о неустойчивости замкнутой
САР.
Пример 2. Исследовать на устойчивость САР, структурная схема которой представлена на рис.7.18, с помощью логарифмического частотного критерия устойчивости.
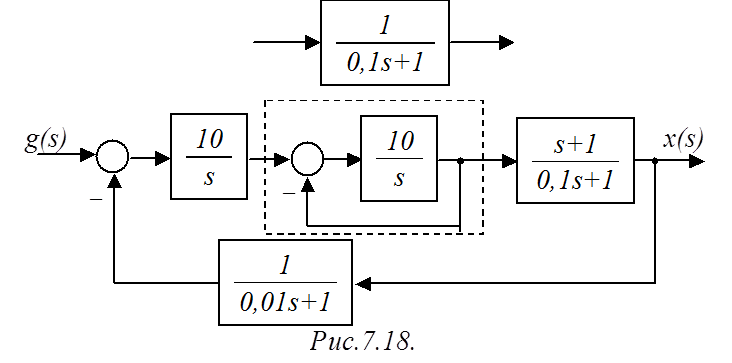
Решение. Преобразовав структурную схему путем свертки внутреннего замкнутого контура, запишем ПФ разомкнутой САР:
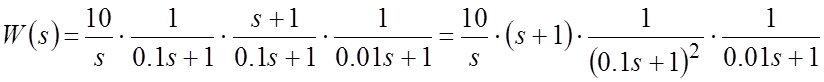 .
.
Строим ЛАЧХ и ЛФЧХ разомкнутой САР (рис.7.19).
Очевидно, ЛФЧХ при частотах, меньших частоты среза, не пересекает уровень –p. Характеристический полином разомкнутой САР не имеет правых корней. Поэтому критерий устойчивости выполняется – замкнутая САР устойчива.
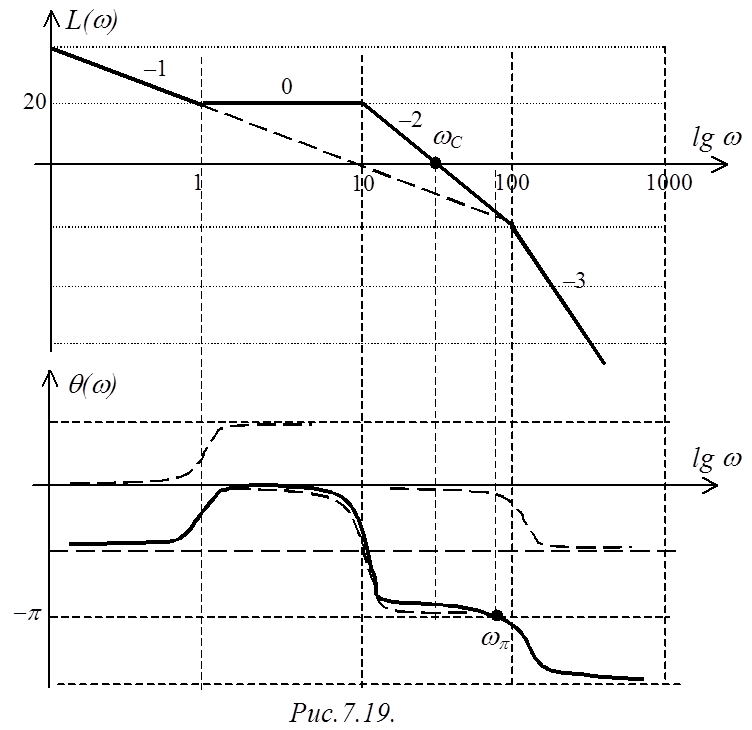 Отметим, что САР будет
иметь недостаточный запас устойчивости по фазе.
Отметим, что САР будет
иметь недостаточный запас устойчивости по фазе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.