Лекция 5
(4 часа)
ТИПОВЫЕ ЗВЕНЬЯ
Любая САР может быть представлена в виде комбинации (последовательного или параллельного соединения) типовых звеньев. К числу типовых звеньев, из которых состоят линейные САР, относятся следующие звенья с ПФ:
1. Усилительное звено ![]()
2. Интегрирующее звено 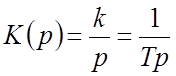
3. Дифференцирующее звено ![]()
4. Апериодическое звено 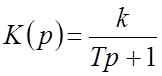
5. Форсирующее звено 1-го порядка ![]()
6. Колебательное звено 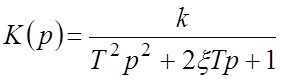 ,
,
![]()
7. Форсирующее звено 2-го порядка ![]()
8. Звено чистого запаздывания ![]()
Усилительное звено (усилитель)
![]()
![]() – коэффициент передачи
– коэффициент передачи
![]()
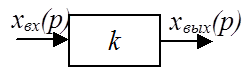 Дифференциальное уравнение
Дифференциальное уравнение
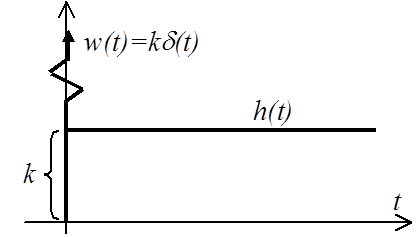
![]() .
.
Переходная функция (см. рисунок)
![]() .
.
Весовая функция (см. рисунок)
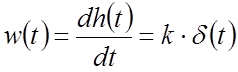 .
.
Частотная характеристика
![]() .
.
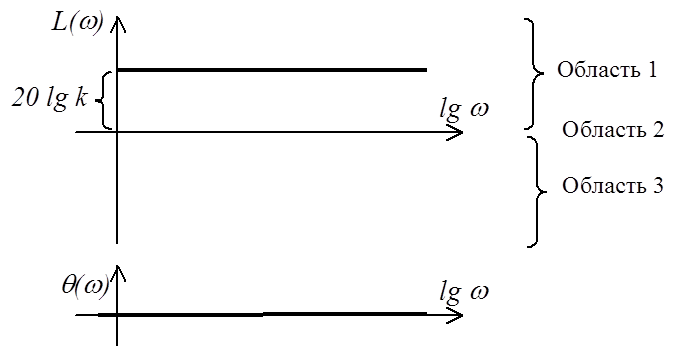 АЧХ
АЧХ
![]() .
.
ФЧХ и ЛФЧХ
![]() .
.
ЛАЧХ
![]() .
.
Область
1 – при ![]()
Область
2 – при ![]()
Область
3 – при ![]()
Интегрирующее звено (интегратор)
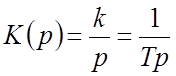
![]() – коэффициент
передачи;
– коэффициент
передачи; ![]() – постоянная времени.
– постоянная времени.
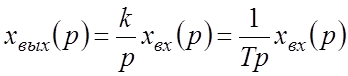
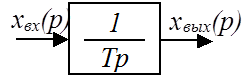 Дифференциальное уравнение
Дифференциальное уравнение
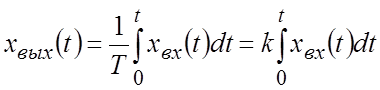 .
.
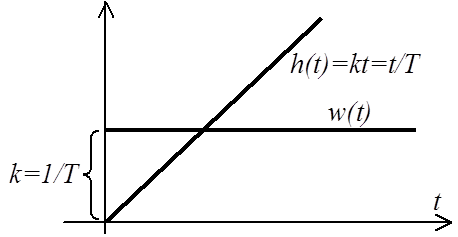 Переходная функция (см. рисунок)
Переходная функция (см. рисунок)
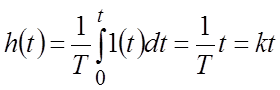 .
.
Весовая функция (см. рисунок)
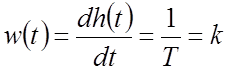 .
.
Применительно
к нашей специальности для интегратора чаще используется понятие постоянной
времени ![]() .
.
При наличии на входе интегратора постоянного сигнала, отличного от нуля, сигнал на его выходе изменяется по линейному закону, при равенстве сигнала на входе нулю сигнал на выходе интегратора стабилизируется и в общем случае отличен от нуля.
Частотная характеристика 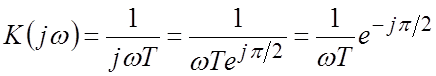 .
.
АЧХ 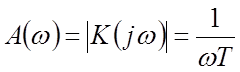 .
.
ФЧХ ![]() .
.
Таким образом, в интеграторе выходной сигнал отстает от входного по фазе на p/2, независимо от частоты w.
ЛАЧХ 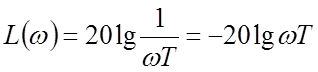 .
.
ЛФЧХ ![]() .
.
ЛАЧХ при какой-то определенной частоте w1 равна L(w1)= –20 lgw1T. При увеличении частоты в 10 раз (на одну декаду) L(10w1) = –20 lg 10w1T = –20 lgw1T – 20. Поскольку L(w1) – L(10w1) = 20 дБ, следовательно, ЛАЧХ интегрирующего звена представляет собой прямую с наклоном –20 дБ/дек.
Построение ЛАЧХ производим по характерным точкам (см. рисунок):
· при w=1 L(w)= –20 lg T = 20 lg 1/T = 20 lg k.
· при w=1/TL(w)=0.
Наклон ЛАЧХ –20 дБ/дек соответствует наклону АЧХ –1, поэтому его часто так и обозначают.
Как уже отмечалось, ЛФЧХ не зависит от частоты и представляет собой прямую на уровне –p/2.
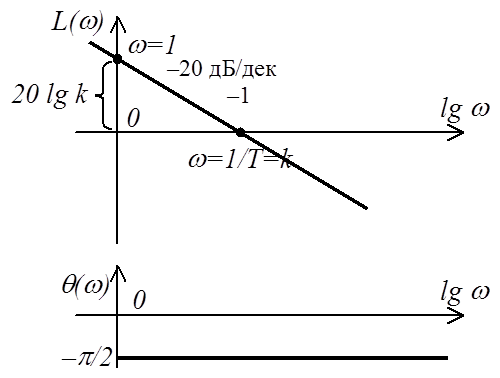 При
При ![]() , как следует из
АЧХ и ЛАЧХ, коэффициент передачи интегратора по амплитуде стремится к
бесконечности; и напротив, при увеличении частоты коэффициент передачи по
амплитуде уменьшается. Это означает, что интегратор не пропускает на выход
высокие частоты, являясь фильтром низких частот.
, как следует из
АЧХ и ЛАЧХ, коэффициент передачи интегратора по амплитуде стремится к
бесконечности; и напротив, при увеличении частоты коэффициент передачи по
амплитуде уменьшается. Это означает, что интегратор не пропускает на выход
высокие частоты, являясь фильтром низких частот.
Дифференцирующее звено (дифференциатор)
![]()
![]() – постоянная
времени
– постоянная
времени
![]()
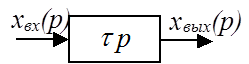 Дифференциальное уравнение
Дифференциальное уравнение
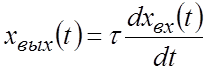 .
.
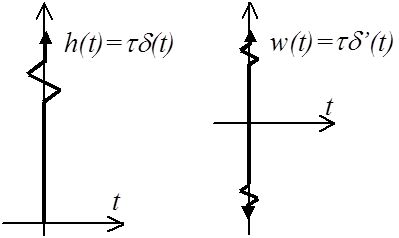 Переходная функция (см. рисунок)
Переходная функция (см. рисунок)
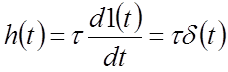 .
.
Весовая функция (см. рисунок)
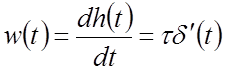 .
.
Частотная характеристика ![]() .
.
АЧХ ![]() .
.
ФЧХ ![]() .
.
Таким образом, в дифференциаторе выходной сигнал опережает входной по фазе на p/2, независимо от частоты w.
ЛАЧХ ![]() .
.
ЛФЧХ ![]() .
.
Аналогично тому, как это было сделано для интегратора,
можно показать, что ЛАЧХ дифференцирующего звена представляет собой прямую с
наклоном +20 дБ/дек (+1), которая будет пересекать ось частот при ![]() (см. рисунок).
(см. рисунок).
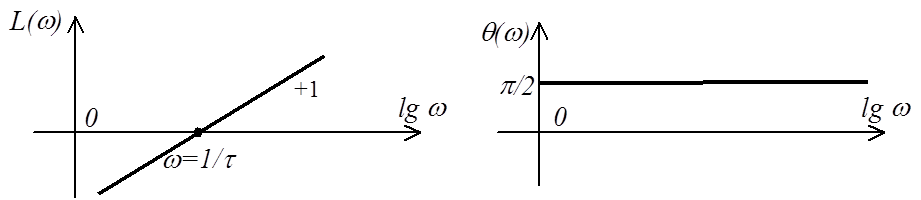
Из ЛАЧХ видно, что с ростом w увеличивается коэффициент передачи дифференциатора по амплитуде. Таким образом, данное звено является помехонеустойчивым в том смысле, что оно подчеркивает высокочастотные помехи (наиболее частые на практике): даже при малой входной амплитуде высокочастотного сигнала на выходе можно наблюдать значительную высокочастотную составляющую.
Примечание.
ПФ дифференцирующего звена является обратной по отношению к передаточной
функции интегрирующего звена. Кроме того (точнее, следовательно), ЛАЧХ и ЛФЧХ
дифференциатора являются зеркальными отображениями соответствующих
характеристик интегратора относительно оси частот. На основании этого можно
сделать более широкий вывод: логарифмические частотные характеристики
любого звена с ПФ ![]() являются обратными
соответствующим характеристикам звена с ПФ
являются обратными
соответствующим характеристикам звена с ПФ ![]() ,
то есть, являются их зеркальными отображениями относительно оси частот w.
,
то есть, являются их зеркальными отображениями относительно оси частот w.
Апериодическое звено (инерционное)
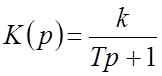
![]() – коэффициент
передачи;
– коэффициент
передачи; ![]() – постоянная времени
– постоянная времени
![]()
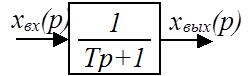 Дифференциальное уравнение
Дифференциальное уравнение
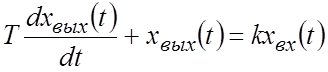 .
.
Найдем сначала импульсную переходную функцию, зная ее
связь с ПФ и используя теорему разложения. ПФ содержит один полюс ![]() , следовательно,
, следовательно,
![]() ,
, 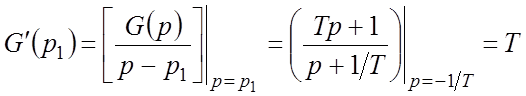
и
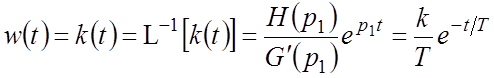 .
.
Переходная функция (см. рисунок)
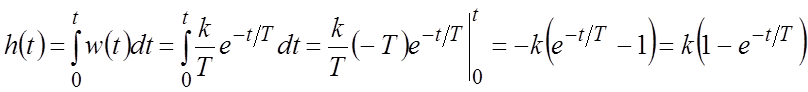 .
.
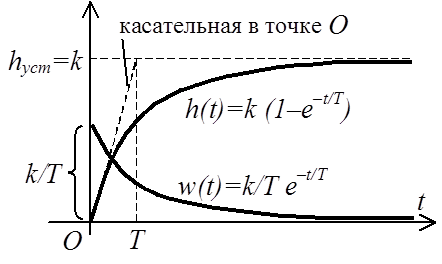 Используя выражение для переходной функции, можно
определить:
Используя выражение для переходной функции, можно
определить:
h(T) = 0,632 k = 0,632 hуст
h(2T) = 0,865 hуст
h(3T) = 0,950 hуст
h(4T) = 0,982 hуст
Таким образом, переходный процесс практически
закончится при ![]() .
.
Постоянная времени T является мерою инерционности апериодического звена. Чем меньше значение Т, тем быстрее протекает переходный процесс.
Частотная характеристика
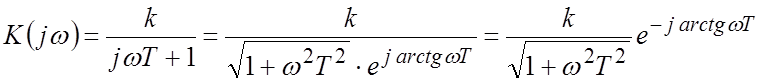 .
.
АЧХ 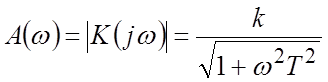 .
.
ФЧХ ![]() .
.
Таким образом, в апериодическом звене фазовый сдвиг зависит от частоты, причем максимальный фазовый сдвиг будет равен –p/2 при w®¥.
ЛАЧХ 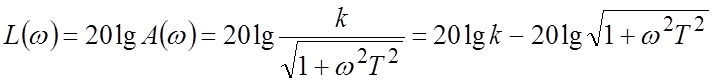 .
.
ЛФЧХ ![]() .
.
Логарифмические частотные характеристики (ЛЧХ) усилительного, интегрирующего и дифференциального звеньев являются прямыми линиями, и легко могут быть построены. Построение ЛЧХ апериодического и остальных звеньев требует вычислений, которые без использования ЭВМ достаточно трудоемки. Поэтому в большинстве случаев на практике ограничиваются построением приближенных асимптотических ЛЧХ, на основании которых уже могут быть сделаны все основные выводы о динамических свойствах звена.
Рассмотрим алгоритм построения асимптотических ЛАЧХ и ЛФЧХ апериодического звена.
Асимптотическая ЛАЧХ. При малых частотах ![]() второе слагаемое
под радикалом
второе слагаемое
под радикалом ![]() , и им можно пренебречь;
тогда
, и им можно пренебречь;
тогда ![]() . При больших частотах
. При больших частотах ![]() под радикалом можно пренебречь единицей
по сравнению с
под радикалом можно пренебречь единицей
по сравнению с ![]() , и тогда
, и тогда ![]() . Таким образом, асимптотическая ЛАЧХ
состоит из двух отрезков, пересекающихся на оси частот в точке, соответствующей
частоте
. Таким образом, асимптотическая ЛАЧХ
состоит из двух отрезков, пересекающихся на оси частот в точке, соответствующей
частоте ![]() , называемой частотой сопряжения
(см. рисунок). Реальная ЛАЧХ апериодического звена (показана пунктиром) имеет
максимальное отличие от асимптотической (3 дБ) при частоте сопряжения.
, называемой частотой сопряжения
(см. рисунок). Реальная ЛАЧХ апериодического звена (показана пунктиром) имеет
максимальное отличие от асимптотической (3 дБ) при частоте сопряжения.
Асимптотическая ЛФЧХ. При частоте сопряжения ![]()
![]() . При малых
. При малых ![]()
![]() , а при больших
, а при больших ![]()
![]() .
На практике при частотах, близких к частоте сопряжения (±1 декада) ЛФЧХ может без большой погрешности заменена линейной зависимостью,
проходящей через точку
.
На практике при частотах, близких к частоте сопряжения (±1 декада) ЛФЧХ может без большой погрешности заменена линейной зависимостью,
проходящей через точку ![]() (см. рисунок).
(см. рисунок).

Форсирующее звено 1-го порядка
![]()
![]() – постоянная
времени
– постоянная
времени
![]()
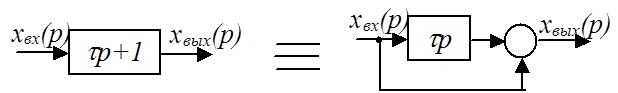
Из эквивалентной схемы видно, что это звено подает на выход входной сигнал и его производную.
Дифференциальное уравнение
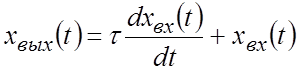 .
.
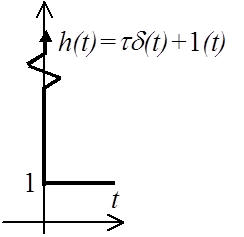 Переходная функция (см. рисунок)
Переходная функция (см. рисунок)
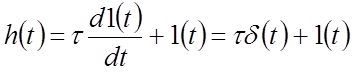 .
.
Весовая функция:
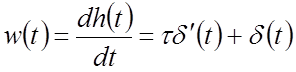 .
.
Частотная характеристика
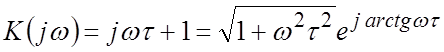 .
.
АЧХ 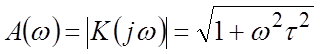 .
.
ФЧХ ![]() .
.
Как и дифференцирующее звено, форсирующее звено 1-го порядка является помехонеустойчивым, поскольку усиливает высокочастотные составляющие входного сигнала.
ЛАЧХ 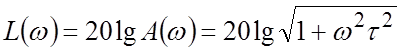 .
.
ЛФЧХ ![]() .
.
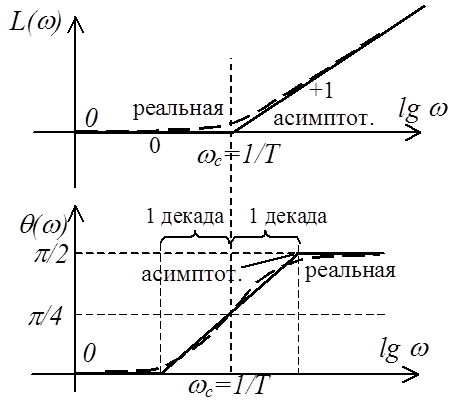 Поскольку ПФ форсирующего звена 1-го порядка обратна
ПФ апериодического звена (при k=1), то ЛЧХ
форсирующего звена являются зеркальным отображением относительно оси частот
соответствующих характеристик апериодического звена при k=1 (см. рисунок).
Поскольку ПФ форсирующего звена 1-го порядка обратна
ПФ апериодического звена (при k=1), то ЛЧХ
форсирующего звена являются зеркальным отображением относительно оси частот
соответствующих характеристик апериодического звена при k=1 (см. рисунок).
Колебательное звено
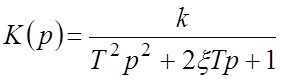
![]() – коэффициент
передачи;
– коэффициент
передачи; ![]() – постоянная времени
– постоянная времени
![]()
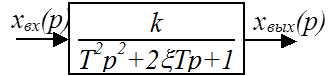
Иногда используют другую форму записи ПФ колебательного звена:
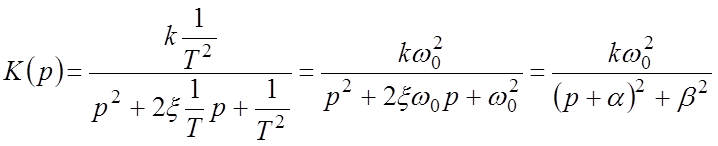 ,
,
где 0<x<1 – коэффициент демпфирования;
![]() – угловая частота колебательного
звена;
– угловая частота колебательного
звена;
a, b – модули действительной и мнимой частей полюсов ПФ колебательного звена.
Доказательство.
Корни уравнения ![]() равны
равны
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.