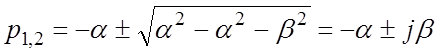Типовые звенья. Комбинации (последовательного или параллельного соединения) типовых звеньев, страница 2

            , поскольку .

Для определения коэффициентов a, b приравняем знаменатели первого и последнего выражений для ПФ:

          .

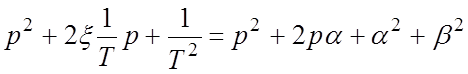Приравнивая коэффициенты при одинаковых степенях p, можно найти:

          ;  ;  .

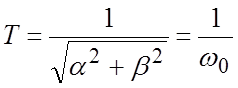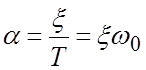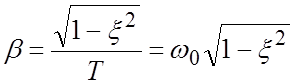Дифференциальное уравнение:

.

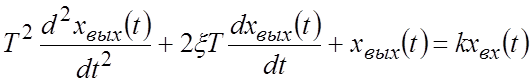Выражения для переходной и весовой функций могут быть выведены с помощью обратного преобразования Лапласа с использованием теоремы разложения при комплексных корнях (примите без доказательства).

Вывод выражения для переходной функции:

.

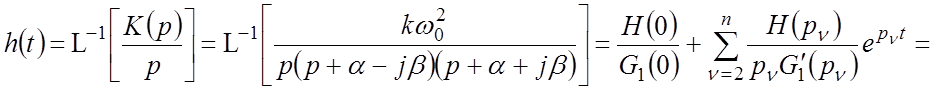
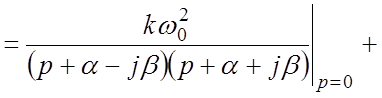
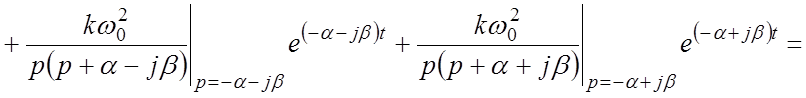
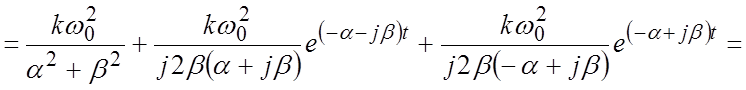
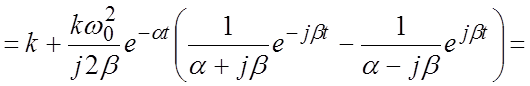
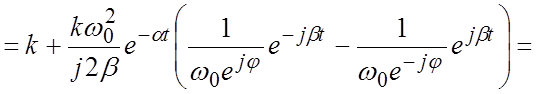
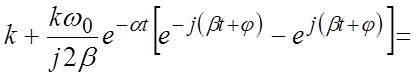
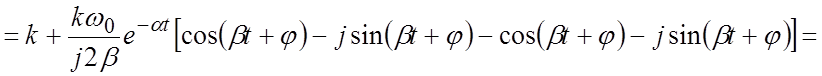
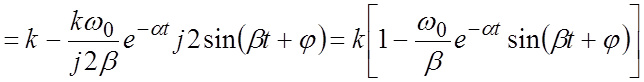Вывод выражения для весовой функции:

.

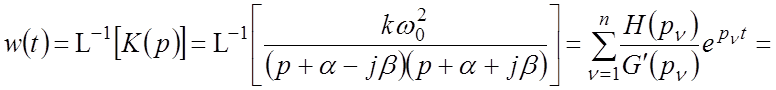
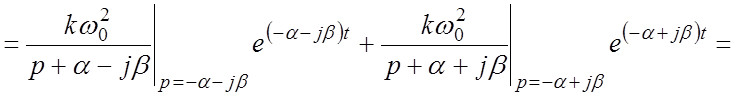
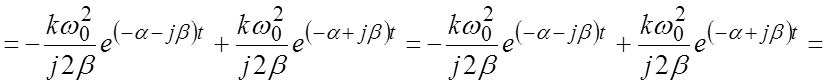
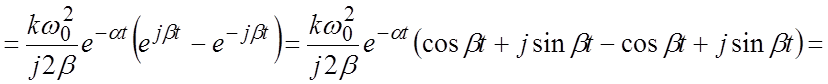
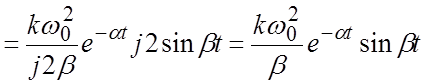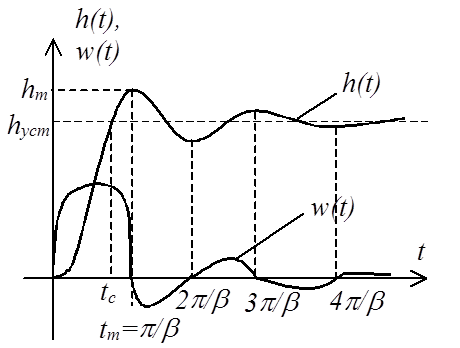
Переходная функция (см. рисунок)

,

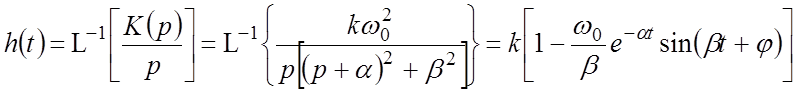где .

Весовая функция (см. рисунок)

.

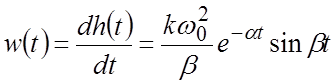Установившееся значение:

          h_уст = k

Значение времени первого согласования t_c можно узнать, если в выражении для переходной функции приравнять синус нулю, тогда , отсюда

          .

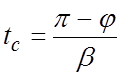Время t_m достижения максимального значения можно узнать, приравняв значение весовой функции нулю:

          .

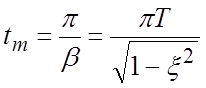Равенство нулю весовой функции будет иметь место также для всех , где  – положительное целое число (см. рисунок).

Подставив t_m в выражение для переходной функции, определим максимальное значение выходной переменной в переходном режиме:

          ,

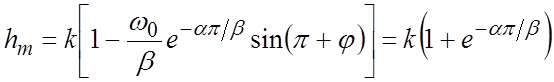где .

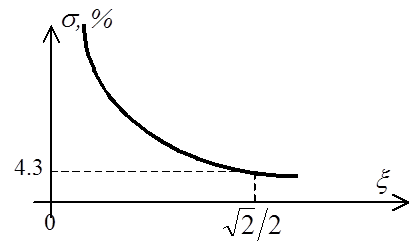
Наконец, перерегулирование

          .

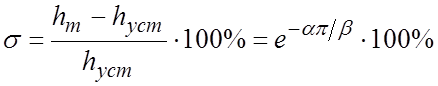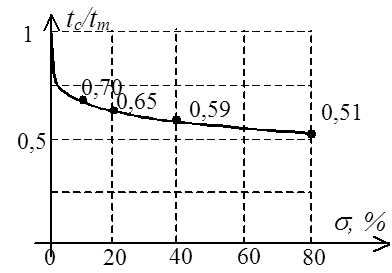
Известны соответствующие графики зависимостей [3]  и :

         

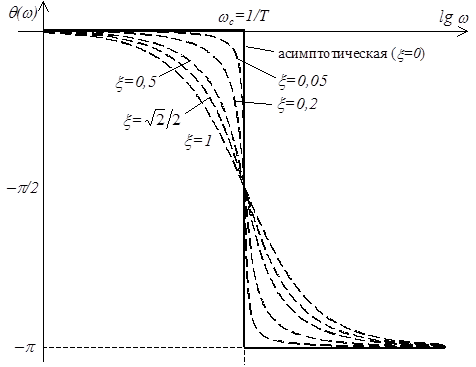
Частотная характеристика:

          .

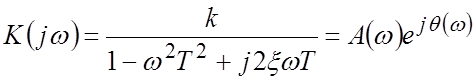АЧХ            .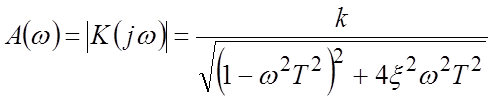

ФЧХ  .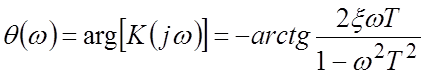

ЛАЧХ          .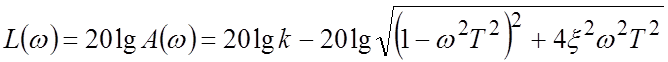

ЛФЧХ         .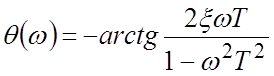

Асимптотическая ЛАЧХ. При малых частотах  можно пренебречь составляющей , тогда . При больших частотах  под радикалом можно пренебречь единицей по сравнению с , и тогда

.

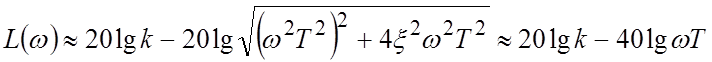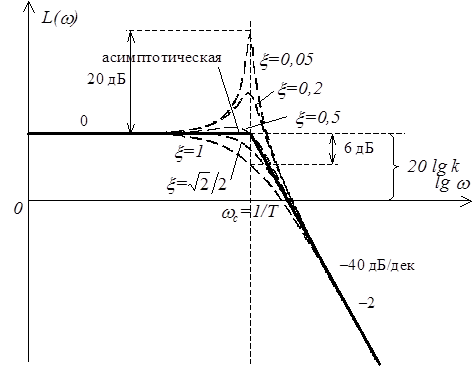
Таким образом, асимптотическая ЛАЧХ колебательного звена состоит из двух отрезков, пересекающихся на оси частот в точке, соответствующей частоте сопряжения  (см. рисунок). Реальная ЛАЧХ достаточна близка к асимптотической (погрешность на частоте сопряжения не превышает 6 дБ) при x=0,2…1,0. В остальных случаях (когда x£0,2) следует воспользоваться либо кривыми поправок [1], либо точным математическим выражением для ЛАЧХ.

Асимптотическая ЛФЧХ. При частоте сопряжения   . При малых  , а при больших  . Но асимптотическая ЛФЧХ совпадает с реальной только при  (см. рисунок), в остальных случаях различие существенное, поэтому следует пользоваться ее математическим выражением.

 

Определение параметров колебательного звена.

Иногда форма записи ПФ колебательного звена может отличаться от стандартных. Возникает вопрос определения параметров Т и x колебательного звена.

Например, ПФ двигателя постоянного тока по управляющему воздействию имеет вид:

          .

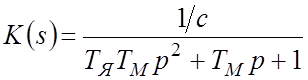Здесь  и . Отсюда

         

          .

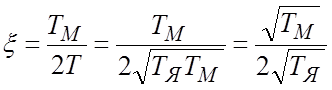Если оказывается, что , имеем колебательное звено. В противном случае () корни знаменателя ПФ становятся действительными, тогда звено представляет собой последовательное соединение двух апериодических звеньев.

Таким образом, значение  говорит о том, какой характер переходного процесса будет иметь место на выходе звена. Применительно к двигателю постоянного тока , когда , и будет иметь место колебательный (с перерегулированием) процесс при скачкообразном приложении управляющего воздействия. В противном случае  переходный процесс будет апериодическим (с дотягиванием).

Форсирующее звено 2-го порядка

 – постоянная времени

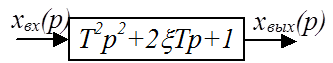
Имеет ПФ, обратную ПФ колебательного звена при , . Поэтому здесь вкратце приведем основные математические зависимости.

Дифференциальное уравнение:

.

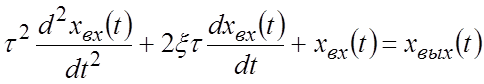Частотная характеристика:

            .

АЧХ               .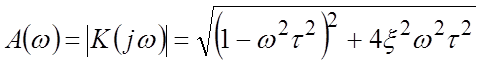

ФЧХ               .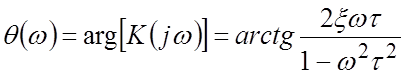

ЛАЧХ .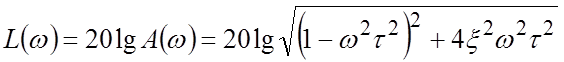

ЛФЧХ .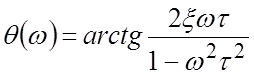

Звено чистого (транспортного) запаздывания

Некоторые ОУ могут обладать запаздыванием (например, трубопроводы, длинные линии, транспортеры). Запаздывание проявляется в том, что при изменении входного воздействия выходная переменная начинает изменяться не сразу, а спустя некоторый промежуток времени t, называемый временем чистого или транспортного запаздывания.

            .

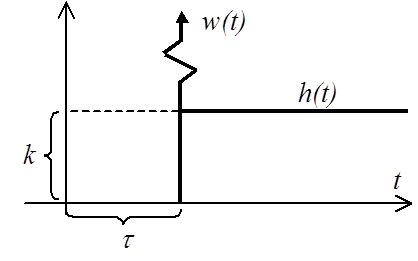Переходная функция (см. рисунок)

           

Весовая функция (см. рисунок)

           

Частотная характеристика:

АЧХ    .

ФЧХ   .

ЛАЧХ .

ЛФЧХ .

Построение логарифмических частотных характеристик

произвольной совокупности типовых звеньев

Пусть имеется произвольное последовательное соединение n типовых звеньев с результирующей ПФ

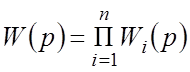                                      (1)

По определению ЛАЧХ и ЛФЧХ вычисляются следующим образом:

          ;

          .

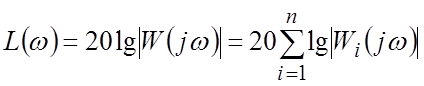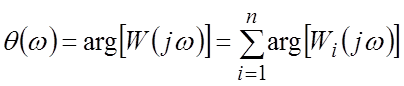Таким образом, для построения ЛАЧХ или ЛФЧХ последовательного соединения звеньев следует построить соответствующие характеристики каждого звена, и затем геометрически их сложить.

Передаточную функцию (1) совокупности звеньев целесообразно представить в более развернутом виде:

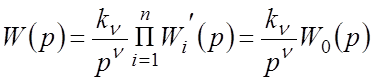              ,                        (2)

где  – нормированная ПФ – отношение произведений ПФ элементарных звеньев 1-го и 2-го порядков (т.е., вида  и  при ) с единичным передаточным коэффициентом ();

       – результирующий коэффициент передачи (усиления);

       – порядок астатизма ПФ (так наз. апериодической нейтральности), численно равный количеству последовательно соединенных интеграторов в предположении, что чистые дифференцирующие звенья отсутствуют.

Пример. Построить асимптотические ЛАЧХ и ЛФЧХ звена с ПФ

            ,

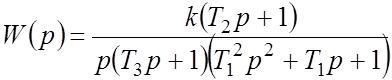где значение коэффициента усиления и постоянных времени известны, и известно, что .

Если рассматривать эту ПФ в виде (2), то

            ;      ;            .

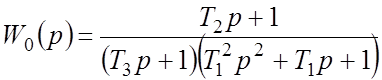Очевидно, имеем последовательное соединение четырех типовых звеньев: интегратор с ПФ ; форсирующее звено 1-го порядка с ПФ ; апериодическое звено с ПФ 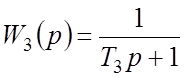; колебательное звено с ПФ  ().

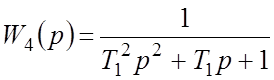Строим асимптотические ЛАЧХ каждого из звеньев (пунктирные линии) и их геометрическую сумму (сплошная линия), которая и является результирующей ЛАЧХ. Аналогично поступаем с ЛФЧХ.

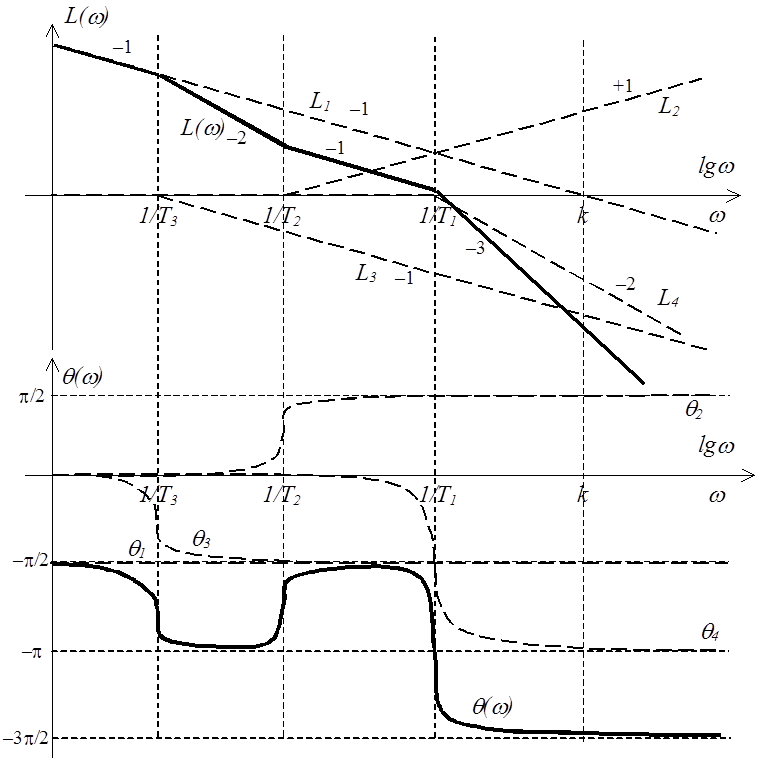
После анализа ЛАЧХ можно предложить следующее правило:

1) Пользуясь представлением (2) передаточной функции, вычисляют все частоты сопряжения  (i = 1, 2, …), которые нумеруют в порядке возрастания и откладывают на оси частот;

2) Предварительную ЛАЧХ начинают строить от области низких частот, проводя прямую под наклоном –20 дБ/дек () так, чтобы она (или ее продолжение) пересекала ось частот при частоте . (Эта ЛАЧХ будет пересекать ось ординат в точке .)

Именно такой вид будет иметь ЛАЧХ совокупности  последовательно соединенных интеграторов, соответствующая первому множителю ПФ вида (2).

3) Низкочастотная ЛАЧХ будет претерпевать изломы только при частотах сопряжения , причем наклон будет изменяться на 20 дБ/дек (+1), если -м звеном оказывается форсирующее звено 1-го порядка, на –20 дБ/дек (–1) – если апериодическое звено, на +40 дБ/дек (+2) – если форсирующее звено 2-го порядка, на –40 дБ/дек (–2) – если колебательное звено.

Что касается ЛФЧХ, то следует построить ЛФЧХ отдельных звеньев, и затем геометрически их просуммировать.

Примечание. В случае наличия последовательно соединенного звена чистого запаздывания ЛАЧХ соединения остается без изменения, однако это звено окажет влияние на фазовый сдвиг.

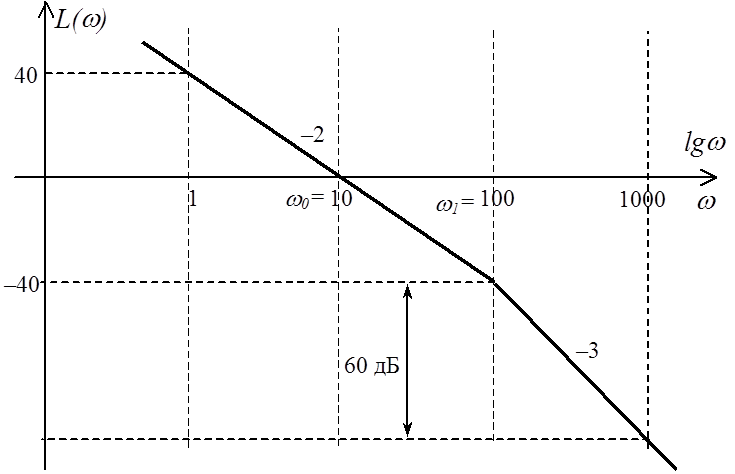
Пример. Пользуясь правилом, построить ЛАЧХ соединения звеньев с ПФ:

           

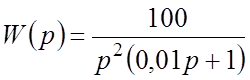
Очевидно, что здесь , , .

Тогда , . Проводим прямую под наклоном –2 (–40 дБ/дек), которая будет пересекать ось частот в точке . При  ЛАЧХ изменит наклон на –1, поскольку  соответствует частоте сопряжения апериодического звена. Следовательно, при  ЛАЧХ будет иметь наклон –3 (–2–1=–3).