Системы и элементы систем. Классификация САУ. Воздействие на систему (переменные системы уравнения). Математические модели непрерывных динамических систем. Метод малых отклонений

(1)Системы и элементы систем

САУ - состоит из объекта управления, управления устройства взаимодействующих между собой (САП). Объект управления (ОУ) – устройство требуемое режим работы которого должен поддерживаться системой. Устройство управления – это устройство, осуществляющее воздействие на объект управления с целью поддерживания режима его работы. Система – это совокупность взаимодействующих между собой элементов. Свойство системы отличается от совокупности элементов, которые в нее входят. При анализе, синтезе систем используют математическое описание СУ. Существует 2 способа мат. описания системы уравления:1)классический – в этом случае все элементы системы описываются с помощью отдельных уравнений без учета взаимосвязи между элементами. 2)системный – в этом случае все элементы систем рассматриваются на конечное число подсистем, и рассматриваются с учетом взаимосвязи между элементом. Математическое описать систему можно 3 способами: 1)аналитический – с помощью диф. или линейных; 2)графический – диаграммы, графики; 3)табличный – график в таблице.

(2)Классификация САУ

Линейные системы – системы которые описываются линейным уравнением. Нелинейные системы – описываются нелинейными уравнениями, т.е. дифференциальными. Непрерывные системы – состояние, которое задано на всем непрерывном множестве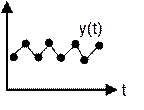. Дискретные системы – системы, значения выходной величины, которая существует или определена в конкретный момент времени 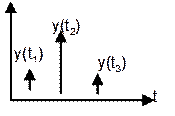. Непрерывно-дискретная система, у которой выходная величина на определенном участке представляет собой непрерывную величину, и на промежутке t₁-t₂ представляет собой дискретную величину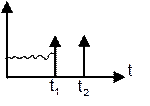. Стационарные системы – системы, которые описываются уравнениями с постоянными параметрами (параметры не изменяются во времени). Нестационарные – описываются уравнениями с переменными параметрами. ССП – системы с сосредоточенными параметрами – системы, которые описываются обыкновенными диф.уравнениями в частных производных. Одномерные – системы, в которых выходная величина одна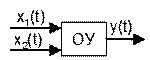. Многомерные – имеют несколько выходных величин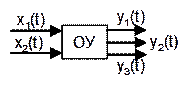. Статические – без инерционные системы, т.е. постоянна во времени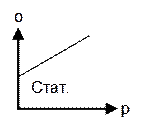. Динамические – входная величина изменяется во времени, для таких величин характерен динамический процесс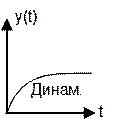. Детерминированные – системы без внешних воздействий. Стохастические (вероятные или случайные) – для таких систем характерно несколько состояний и все она зависит от внешних воздействий.

(3)Воздействие на систему (переменные системы уравнения).

Задающее воздействие или входное воздействие х(t) – это воздействия которое планируется. Управляющее воздействие (U(t)) – воздействие обусловлено управляющим уравнением и оказывает влияние на субъекты управления. Возмущающие воздействия f(t) – воздействие не планируемое, т.е. случайное (параметры окружающей среды). Выходное у(t) – управляемое переменной, данная величина характеризует параметры объекты управления. Внутреннее x(t) – обусловлено влиянием одних систем на другие.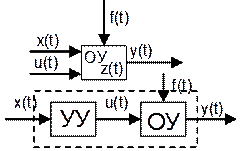

(4)Математические модели непрерывных динамических систем.

Прежде чем приступать к мат.модели САУ необходимо составить ее функциональную схему. В такой схеме каждому элементу САУ соответствует некоторый прямоугольник с обозначением данного конкретного элемента. 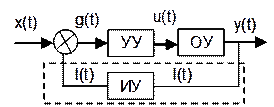Входное воздействие поступает на сумматор с учетом обработки ошибки из входного воздействия получается задающее воздействие g(t). Поступив на устройство управления вырабатывая управляющее воздействие u(t) и поступает на объект управления. В объекте управления с учетом внешнего воздействия j(t) вырабатывает выходная у(t). Ошибка регулирования, которая l(t) поступает на исполнительное устройство, которое предназначено для изменения состояний рассомасования. Данная система является замкнутой. Нижняя часть называется обратной связью, которая может быть и положительной и отрицательной. На следующем этапе составления математической модели функциональная схема преобразуется в структурную схему, которая состоит также из прямоугольников, но вместо обозначения элемента системы в него записывается уравнение состояния или работы данного звена. Структурная схема является математической моделью системы управления. Уравнения, которые описывают изменяющиеся во времени состояния системы или элемента называются уравнениями динамики. Чаще всего системы описываются с помощью диф.уравнений.

(5)Метод малых отклонений.

При исследовании нелинейной системы уравнений решение можно получить лишь в чистом виде, поэтому для получения аналитического решения нелинейных диф.уравнений используют линеализацию. Линеализация – замена нелинейных уравнений приближенными линейными уравнениями (метод малых отклонений). Рассмотрим некоторый элемент 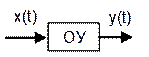. Пусть между входной и выходной величиной осуществляются процессы, которые описываются нелинейным дифференциальным уравнением вида 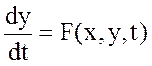. Обозначим установившееся состояние объекта через х₀, у₀ и отклонение от данного состояния х’ и у’. тогда входная величина будет представлена: х=х₀+х’; y+y₀+y’. В общем случае входная и выходная величины могут являться функциями времени, тогда выходная величина будет представлена: 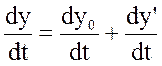. В окрестностях точки х₀, у₀ функцию F(x,y,t) разложим в ряд Тейлора: 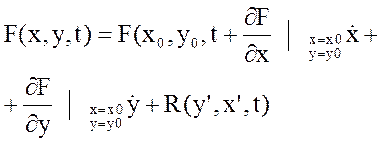, где R – совокупность членов ряда, порядок производной которой выше первой. В случае, если отклонение от установившегося, значения малы можно получить 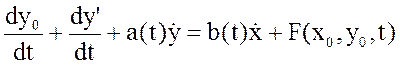(*), где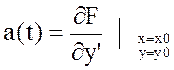 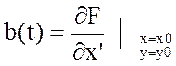. В том случае, если отклонение от установившегося состояния равны 0, уравнение будет выглядеть 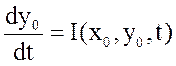(**). Вычитая (**) из (*) получаем линейное диф.уравнение 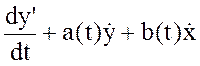, которое называется уравнением в отклонениях. Это уравнение описывает состояние объекта управления при малых отклонениях.

(6)Метод решений диф.уравнений.

1)аналитический, получают решение в явном виде. На основе данного решения можно исследовать реакцию объекта на любые входные воздействия; 2)численный, решением уравнения является числовое решение при заданных начальных условиях; 3)качественный, используется в основном в теории управления и не имея решения в явном виде получают различные качественные оценки?????(время переходного процесса, полоса пропускания). Этапы решения диф.уравнений: 1)по исходному диф.уравнению составляют характеристическое уравнение системы; 2)находят корни характеристического уравнения; 3)записывают общие решения диф.уравнений и используя начальные условия определяют коэффициенты выходной величины; 4)к общему решению диф.уравнения прибавляют частное решение. Однако нахождение корней характеристического уравнения, порядок которого выше третьей степени аналитически не возможно, поэтому для нахождения корней используют численные методы, что усложняет исследование системы в целом.

(7)Способы записи передаточных функций.

Для исследования систем высокого порядка используют операторный метод, который основан на преобразованиях Лапласа и который называется методом передаточных функций системы. Передаточной функцией системы или элемента называется отношение выходной величины системы к входной 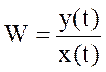. Существует 4 способа определения передаточных функций:1)операторный; 2)стандартная форма; 3)форма передаточной функции в изображениях по Лапласу; 4)частотная форма передаточной функции.

(8)Свойства преобразования Лапласа.

1)теорема подобия ,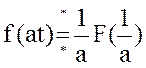

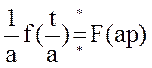
2)

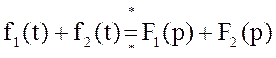
3)af(t)=aF(p)

4)если оригинал функции смещается вдоль оси на некоторую величину τ, то изображение от данной функции j(t-τ)e^-τpF(p)

5)если оригинал функции умножается на величину ep^0t, то изображение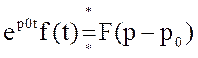

6)теорема свертки

7)

8)

9)

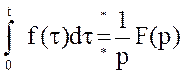
10)

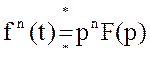
(9)Виды входных воздействий.