Системы и элементы систем. Классификация САУ. Воздействие на систему (переменные системы уравнения). Математические модели непрерывных динамических систем. Метод малых отклонений, страница 2

Различают детерминированное и случайные входные воздействия. Детерминированные воздействия делятся на ступенчатое, импульсное, гармоническое. Функция, зависящая от времени и описывающая реакцию системы или элемента на некоторое входное воздействие называется откликом элемента или системы. 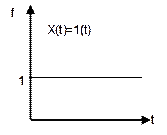 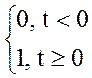Функция которая описывает реакцию системы на единичном входе, воздействие называется переходной функцией или элемента (h(t)). Нахождение h(t): 1)непосредственно из дифференциального уравнения 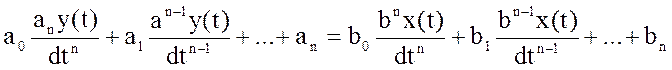; x(t)→1(t); y(t)→h(t). 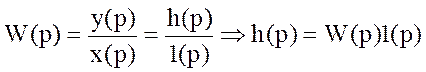;  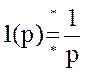; ; 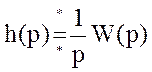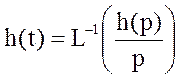. 2)импульсное воздействие представляет собой 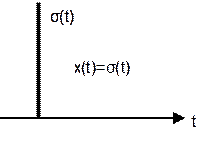 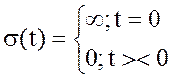Функция, описывающая реакции системы на импульсное воздействие называется весовой функцией элемента или системы (ω(t)). Методы нахождения ω(t): 1)непосредственно из диф.урав. y(t)→ω(t); x(t)→σ(t). 2)используя преобразования Лапласа: 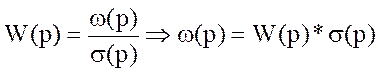, , 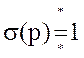ω(p)=W(p), ω(t)=L^-1(W(p)). Гармоническое воздействие: частотные характеристики системы или элемента, полученные при подаче на вход гармонического воздействия описывают установившееся вынужденные колебания, вызванные подачей на вход воздействия вида: x=x_msin(ωt), x_m-амплитуда сигнала. Выходная величина: y(t)=y_{переходная}(t)+у_{установшееся}(t), y(t)=Y_msin(ωt+φ). В показательной форме входных и выходных переменные: x=x_me^jωt; y=Y_me^jωt(φ-φ0).

Прямое преобразование Лапласа: 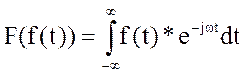. Обратное преобразование Лапласа:  .

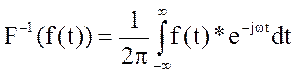(10)Мат. описание дискретных динам. систем.

Система, в которой вместе с нелинейными элементами используются дискретные элементы импульсной системы. С помощью дискретных элементов происходит преобразование сигнала из непрерывного в дискретный сигнал, который называется квантование. Существует 3 вида квантования: 1*по времени, 2*по уровню, 3*по уровню и времени одновременно. Система, в которой осуществляется квантование по времени называется импульсными системами. Система, в которых осуществляется квантование по уровню и по времени называется цифровыми системами. Помимо дискретных элементов импульсная система содержит непрерывную часть, в которой данный дискретный элемент выполняет функцию модулятора. В таких системах импульсная модуляция заключается в переменных одного из выходных параметров импульсного элемента: амплитуда времени импульса и периода импульса. Согласно этому существует 3 оси типа импульсной модуляции (форма импульса может быть любой): 1)амплитуда-импульсная модуляция (АИМ) 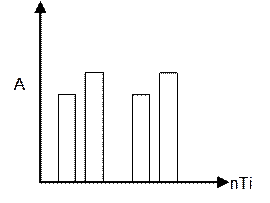 Тк=const, Ti=const. 2)широко-импульсная модуляция (ШИМ) 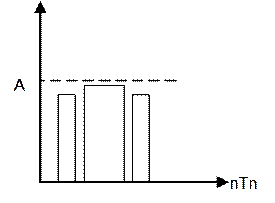 Одинаковая амплитуда, период следования, но разную длительность импульсов А=const, Tn=const. 3)частотно-импульсная модуляция (ЧИМ)       Одинаковая амплитуда, длительность, но разный период следования. A=const, Ti=const. Tn-период следования, А-амплитуда. Дискретные системы могут быть линейными и нелинейными импульсного элемента и непрерывной части не оказывается внешних воздействий, которые зависят от состояния системы. Нелинейной называется если на систему осуществляется внешнее воздействие и состояние импульсного элемента и непрерывной части зависят от состояния систем. Импульсные системы могут быть одномерными и многомерными. Одномерная система в том, случае, если на выходе непрерывной части имеет место одна непрерывная величина. Многомерная – если на выходе имеет место несколько выходных величин. 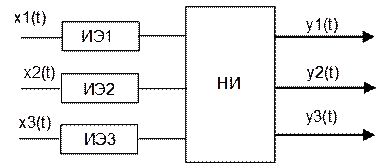 В такой системе могут вырабатываться импульсы различной форму, времени и периода. Если все периоды повторения импульсов в импульсной системе совпадают, такая система называется синхронной, если совпадают и моменты начала импульсов, такая система называется синфазной. Характеристика импульсного элемента, которая отражает зависимость модулируемого сигнала от соответствующих дискретных значений входного сигнала называется импульсной характеристикой элемента или системы. Каждый линейный и импульсный элемент характеризуется коэффициентом передачи 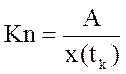, где х(t_k) – значение входного непрерывного сигнала в момент времени t_x, А- амплитуда входного сигнала. Существует понятие: реальный импульсный элемент, который может быть представлен в виде последовательного соединения идеального импульсного элемента и формирующего элемента. 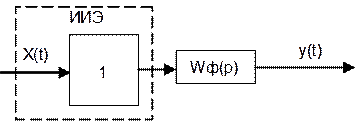 Идеальный импульсный элемент вырабатывает на своем выходе идеальный импульс, т.е. импульсы бесконечно малой длительности и бесконечно большой амплитуды. Формирующий элемент преобразует идеальные импульсы по форме соответствия выходного импульса реального элемента (АИМ, ШИМ, ЧИМ).

(11)Решетчатые функции.

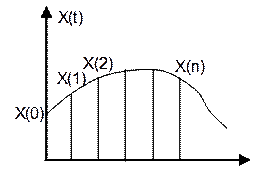 Непрерывная x(t) разбивается на дискретные x(0), x(1)…. Такие функции называются решетчатыми функциями, а исходная непрерывная величина x(t) будет являться огибающее. В случае когда период решетчатой функции Tn=1 решетчатая функция обозначается x[n] и функциональное преобразование решетчатой функции называется дискретным преобразованием Лапласа или Z преобразованием. Когда Tn=1 решетчатая функция обозначается x(t) называется нормализованной. Для нормализованной решетчатой функции дискретное преобразование Лапласа выглядит: 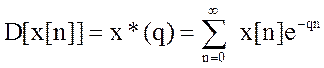 , где q-pTn безразмерная комплексная величина. Для нормализованной Tn≠1 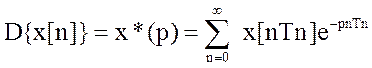. Для решетчатой функции справедливы все свойства преобразования Лапласа. Дискретные системы могут быть описаны с помощью конечно-разностных уравнений. В этом случае производные от непрерывных функций, соответствие конечной разности соответствующих порядков для производных непрерывных функций первого порядка  соответствует конечная разность вида: , . . 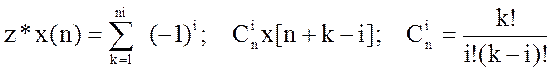Использование конечной разности к-порядка дискретную систему (задана диф. уравнением) можно описать:

a0∆^ky[n]+a1∆^k-1y[n]+…+any[n]=b₀∆^mx[n]+_b1∆^n-1x[n]+…+b_mx[n]. для решения данного уравнения необходимо ввести начальные условия, т.е. y[0], ∆y[0], ∆^k-1y[0], т.е. определить или зафиксировать входную величину в момент времени t. Решая данное уравнение можно определить реакцию дискретной системы на любое входное воздействие. Если данное уравнение линейное, то дискретная система тоже линейная. Линейными дифференциальными уравнениями конечных разностях описываются дискретные системы с АИМ. Нелинейные описываются ШИ и ЧИ модуляцией.

(12)Виды квантования.

1)квантование по времени – при квантовании фиксируется некоторое значение времени Tn. 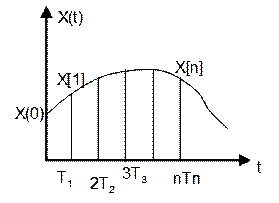 В этих временных интервалах непрерывная функция x(t) разбивается на дискретные функции в момент времени Tn. 2)по уровню – фиксируется величина данного конкретного уровня и данная непрерывная величина разбивается на оси ОУ. 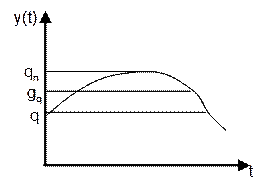 3)по уровню и времени одновременно – задается промежуток времени и фиксируется промежуток q. Заменяется дискретным значением соответствующего угла. 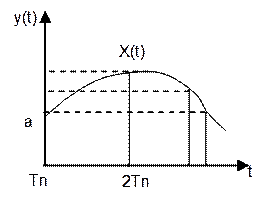При исследовании цифровой системы достаточно часто в их схему входит микропроцесс, который может объединить несколько контуров, регулирующих параметров системы. Если регулирование не связанное, то каждый параметр системы рассматривается в отдельности. В цифровой системе можно выделить непрерывную и дискретную часть. Дискретную часть всех САУ можно в общем виде: ИЭ1 – преобразование непрерывных входных сигналов в дискретные (квантование по времени). КЭ – (кодирующий элемент)осуществляет квантование по уровню. ЦП -                                    (центральный процессор) – преобразовывает один дискретный сигнал в другой по заданному алгоритму. НЭ – (нелинейный элемент) – преобразование кодирующий дискретный сигнал в импульсный. ИЭ2 – (импульсный элемент) разделяет входные и выходные величины и квантует выходную величину по времени. Э – (экстраполятор) преобразует выходную импульсную величину в последовательную ступенчатую функцию. В случае, если квантование по уровню мало или им можно пренебречь, структурная схема цифровой САУ. 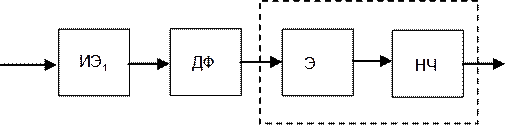 ДФ(дискретный фильтр) – заменяет КЭ, ЦП, ИЭ2, НЭ. Экстраполятор  относится к непрерывным элементам и в совокупности с непрерывной частотой САУ обозначают приведенную непрерывную часть. При экстраполяции выходного сигнала используются различные методы, но чаще всего фиксируется значения амплитуды в момент поступления сигнала и продолжается этот уровень на весь период импульса, т.о. получена последовательная ступенчатая функция.