МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
факультет: ИС
дисциплина: МОТС
СОСТАВЛЕНИЕ ДИФФЕРИНЦИАЛЬНЫХ УРАВНЕНИЙ САУ
Выполнил:
гр. УИТ-32
принял:
г. Балаково 2005 г.
Дана функциональная схема САУ, которая описана 5-ю уравнениями:
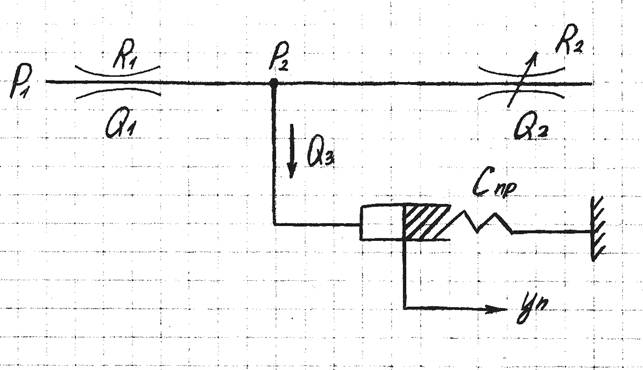
1) ![]()
2) 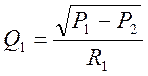
3) 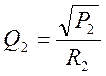
4) 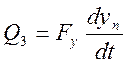
5) 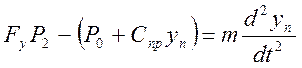
![]() - начальное давление
- начальное давление
![]() - нерегулируемое
гидравлическое сопротивление
- нерегулируемое
гидравлическое сопротивление
![]() - начальный расход
жидкости
- начальный расход
жидкости
![]() - давление на входе
объекта управления
- давление на входе
объекта управления
![]() - расход жидкости
поступающий на объект управления
- расход жидкости
поступающий на объект управления
![]() - регулируемое
гидравлическое сопротивление
- регулируемое
гидравлическое сопротивление
![]() - расход на выходе системы
- расход на выходе системы
![]() - жесткость пружины
- жесткость пружины
![]() - перемещение поршня
- перемещение поршня
![]() - масса поршня
- масса поршня
![]() - начальное
гидростатическое давление на систему
- начальное
гидростатическое давление на систему
![]() - сила действующая на
поршень
- сила действующая на
поршень
Входной величиной системы является![]() , выходной -
, выходной - ![]() . Требуется записать уравнение
системы в виде вход-выход.
. Требуется записать уравнение
системы в виде вход-выход.
Переменные ![]() – нелинейные.
– нелинейные.
Рассмотрим первое уравнение:
![]() для данного уравнения
обозначим
для данного уравнения
обозначим ![]() как сумму установившегося состояния
и отклонения.
как сумму установившегося состояния
и отклонения.
![]()
![]()
![]()
![]() (1)
(1)
Запишем уравнение (1) для установившегося состояния:
![]() , тогда
, тогда ![]() (2) , из уравнения (1) вычтем (2) и
получаем
(2) , из уравнения (1) вычтем (2) и
получаем
![]() (3)
(3)
Рассмотрим второе уравнение:
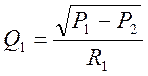 для данного уравнения
обозначим
для данного уравнения
обозначим ![]() как сумму установившегося состояния
и отклонения.
как сумму установившегося состояния
и отклонения.
![]()
![]()
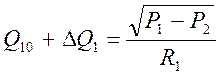 , рассмотрим правую часть
уравнения
, рассмотрим правую часть
уравнения 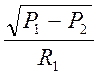 , данная функция является нелинейной,
поэтому ее раскладываем в ряд Тейлора по переменной
, данная функция является нелинейной,
поэтому ее раскладываем в ряд Тейлора по переменной ![]() .
.
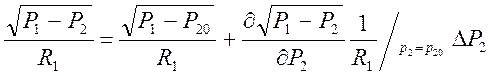
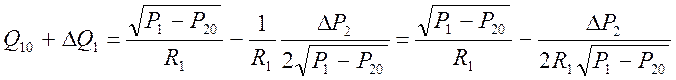 (4)
(4)
Запишем уравнение (4) для установившегося состояния:
![]() , тогда
, тогда 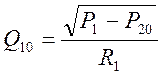 (5), из уравнения (4) вычтем (5) и
получаем
(5), из уравнения (4) вычтем (5) и
получаем
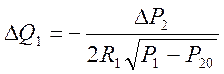 (6)
(6)
Рассмотрим третье уравнение:
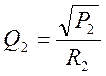 для данного уравнения
обозначим
для данного уравнения
обозначим ![]() как сумму установившегося состояния
и отклонения.
как сумму установившегося состояния
и отклонения.
![]()
![]()
![]()
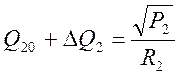 рассмотрим правую часть
уравнения
рассмотрим правую часть
уравнения 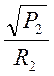 , данная функция является нелинейной,
поэтому ее раскладываем в ряд Тейлора по переменным
, данная функция является нелинейной,
поэтому ее раскладываем в ряд Тейлора по переменным ![]() .
.
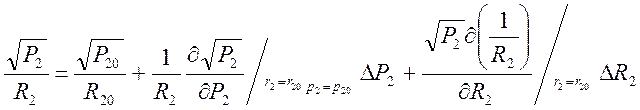
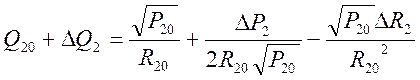 (7)
(7)
Запишем уравнение (7) для установившегося состояния:
![]() , тогда
, тогда 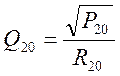 (8) из уравнения (7) вычтем (8) и
получаем
(8) из уравнения (7) вычтем (8) и
получаем
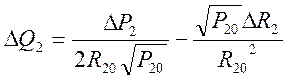 (9)
(9)
Рассмотрим четвертое уравнение:
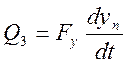 для данного уравнения
обозначим
для данного уравнения
обозначим ![]() как сумму установившегося состояния
и отклонения.
как сумму установившегося состояния
и отклонения.
![]()
![]()
Из уравнения (1) выразим необходимую величину:
![]() , подставим в формулу уже
найденные значения (уравнения 4, 7) и получим:
, подставим в формулу уже
найденные значения (уравнения 4, 7) и получим:
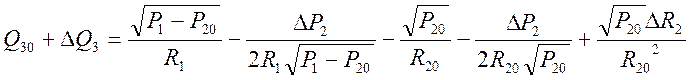
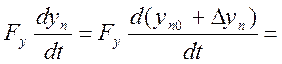
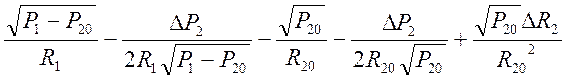 (10)
(10)
Запишем уравнение (10) для установившегося состояния:
![]() , тогда
, тогда 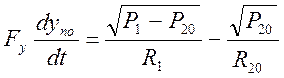 (11) из уравнения (10) вычтем (11) и
получаем
(11) из уравнения (10) вычтем (11) и
получаем 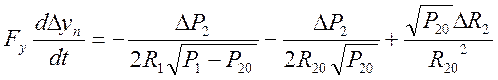 (12)
(12)
Рассмотрим пятое уравнение:
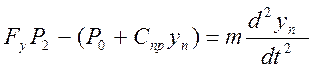 для данного уравнения
обозначим
для данного уравнения
обозначим ![]() как сумму установившегося состояния
и отклонения.
как сумму установившегося состояния
и отклонения.
![]()
![]()
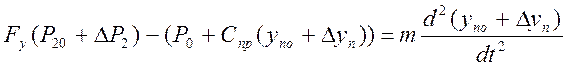 (13)
(13)
Запишем уравнение (13) для установившегося состояния:
![]() , тогда
, тогда 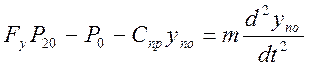 (14) из уравнения (13) вычтем (14) и
получим
(14) из уравнения (13) вычтем (14) и
получим 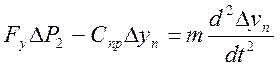 (15) выразим из (15)
(15) выразим из (15) ![]() получим
получим
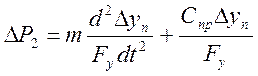 (16) подставим (16) в
уравнение (12) получим
(16) подставим (16) в
уравнение (12) получим
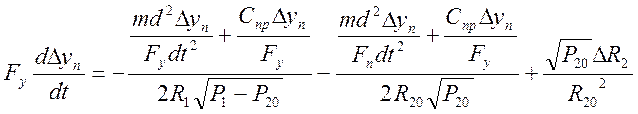
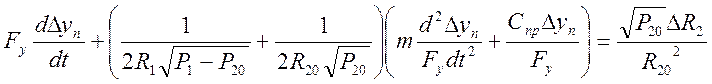 (17)
(17)
Так как входной величиной системы является ![]() , а выходной
, а выходной ![]() ,
то (17) уравнение системы в виде вход-выход.
,
то (17) уравнение системы в виде вход-выход.
Выразим из (15) ![]() :
:
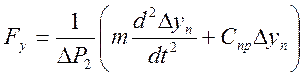 и подставим в (12):
и подставим в (12):
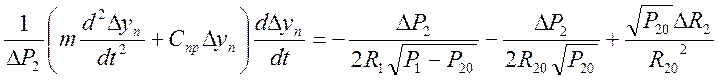 . Так как входной
величиной системы является
. Так как входной
величиной системы является ![]() , а выходной
, а выходной ![]() , то это уравнение системы в виде
вход-выход.
, то это уравнение системы в виде
вход-выход.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.