 |
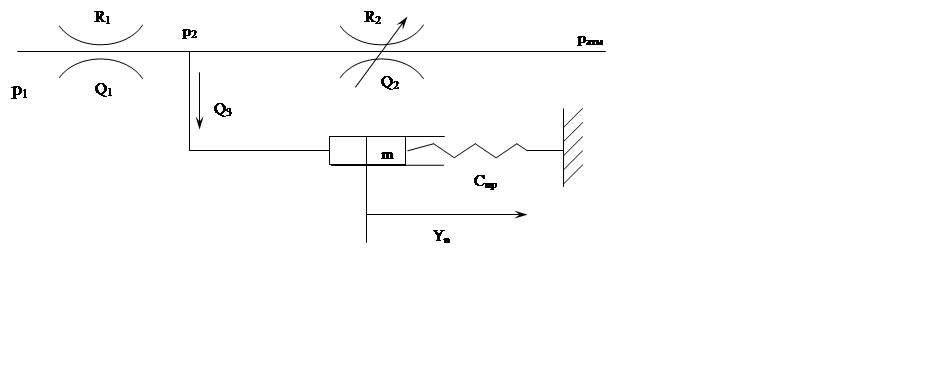
Записать уравнение системы в виде вход – выход:
где R2 – входная величина, а Yп – выходная величина.
1.
![]()
2.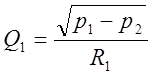
3.
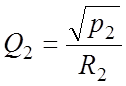
4.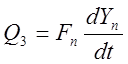
5.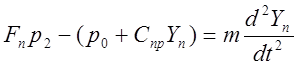
Решение:
1) линеаризуем уравнения (2) с помощью метода малых отклонений:
Обозначим через ![]() и
и ![]() установившиеся
значения,
установившиеся
значения,
а через ![]() и
и ![]() -
малое отклонение величин от установившегося значения.
-
малое отклонение величин от установившегося значения.
Получим:
![]()
![]()
Рассмотрим левую часть уравнения (2):
![]() ;
;
Рассмотрим правую часть уравнения (2):
Для не линейной функции 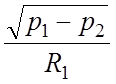 используем разложение в ряд Тейлора:
используем разложение в ряд Тейлора:
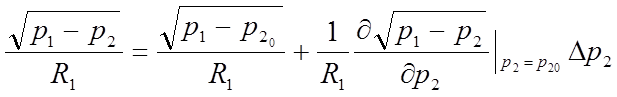
Тогда уравнение (2) примет вид:
![]()
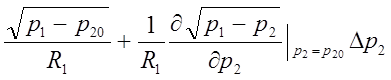
Преобразуем его:
![]()
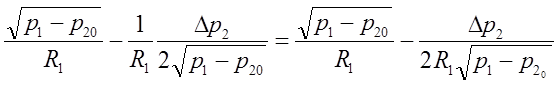 (*)
(*)
Запишем уравнение (*)для установившихся состояний,
т.е. ![]()
Получим:
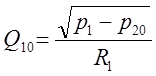 (**)
(**)
Вычтем (**) из (*) и получим уравнение в приращениях:
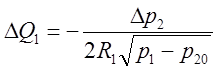 (2’)
(2’)
2) линеаризуем уравнения (3) с помощью метода малых отклонений:
Обозначим через ![]() и
и ![]() ,
и
,
и ![]() установившиеся значения,
установившиеся значения,
а через ![]() ,
, ![]() и
и
![]() - малое отклонение величины от
установившегося значения.
- малое отклонение величины от
установившегося значения.
Получим:
![]()
![]()
![]()
Рассмотрим левую часть уравнения (3):
![]()
Рассмотрим правую часть уравнения (3):
Для нелинейной функции 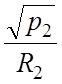 используем
разложение в ряд Тейлора:
используем
разложение в ряд Тейлора:
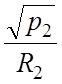 =
=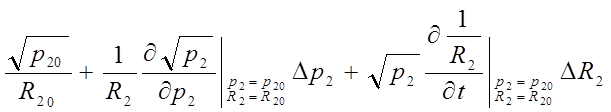
Тогда уравнение (3) примет вид:
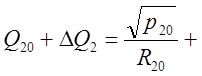
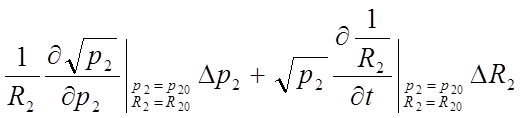
Преобразуем его:
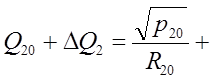
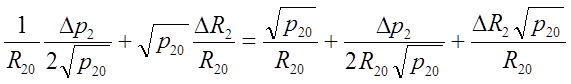 (*)
(*)
Запишем (*) для установившихся значений:
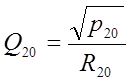 (**)
(**)
Вычтем (**) из (*) и получим уравнение в приращениях:
![]()
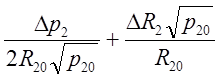 (3’)
(3’)
Перейдем от уравнения (1) к уравнению в приращениях:
Рассмотрим уравнение (1).
Обозначим через ![]() ,
, ![]() ,
, ![]() - установившиеся значения изменяемых
величин, а через
- установившиеся значения изменяемых
величин, а через ![]() ,
, ![]() ,
,
![]() - приращение.
- приращение.
Тогда:
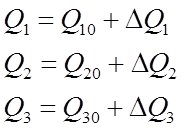
Подставим в уравнение (1):
![]() (*)
(*)
Запишем данное уравнение в установившихся значениях:
![]() (**)
(**)
Вычтем (**) из (*) и получим уравнение в приращениях:
![]() =
=![]() +
+![]() (1’)
(1’)
Аналогично приведётся уравнение (4) и (5) к уравнениям (4’) и (5’), соответственно:
![]()
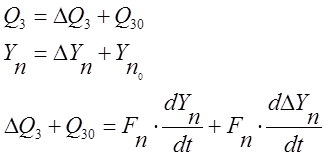
Для установившихся значений:
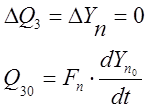
Уравнение в приращениях:
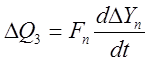 (4’)
(4’)
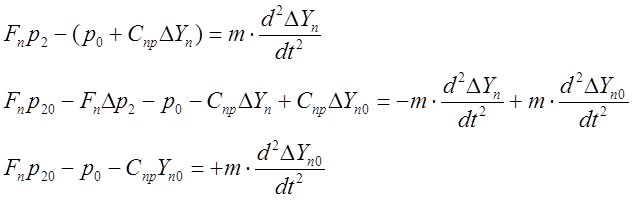
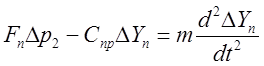 (5’)
(5’)
Подставим уравнения (2’), (3’), (4’) в выражение (1’):
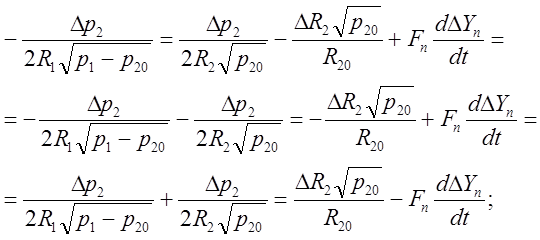 (*)
(*)
Выразим из уравнения (5’) ![]() :
:
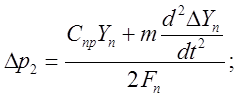 (**)
(**)
Подставим уравнение (**) в выражение (*):
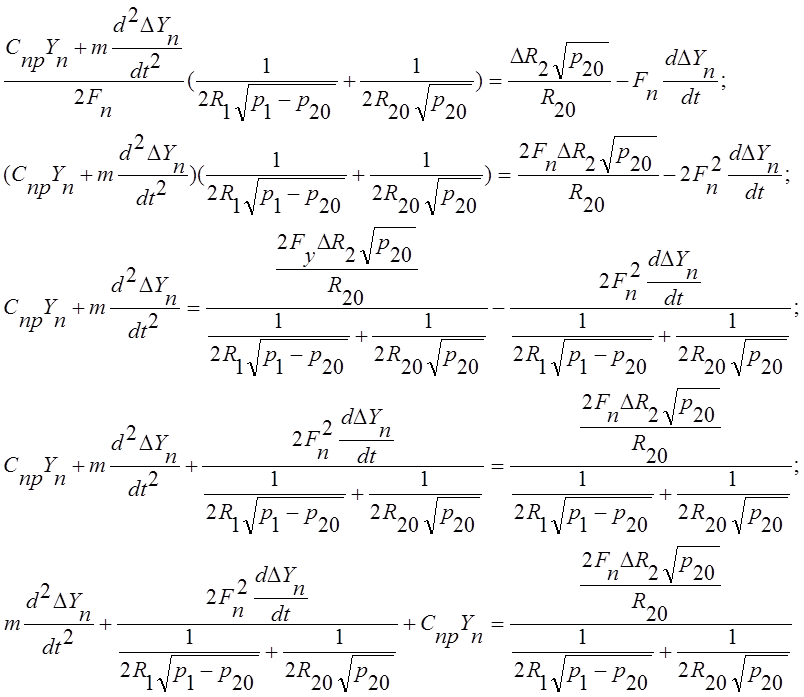
Запишем уравнение в виде вход – выход, для этого R2 ( входная величина) выразим и перенесём влево, а всё остальное и Yп ( выходная величина) вправо
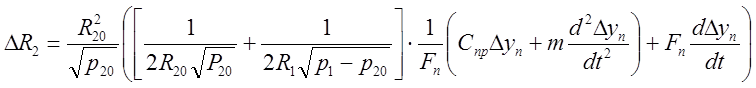
Ответ:
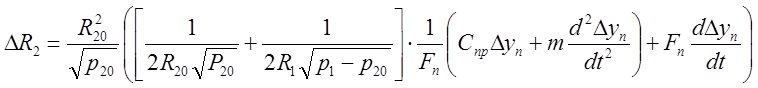
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.