Система. Элементы системы. Математические модели динамических систем. Входные воздействия. Математическое описание объектов или систем с помощью графов. Математическое описание многомерных объектов или систем

Балаковский институт техники, технологии и управления (филиал)

ГОУ ВПО Саратовский государственный технический университет

Факультет инженерно-строительный

ЛЕКЦИИ

по дисциплине «МОТС»

специальности 220201.65-Управление и информатика в технических системах

для студентов очной формы обучения

Автор: к.т.н. доцент Ефремова Т.А.

2010 г.

Содержание.

Система. Элементы системы. 1

Способы математического описания систем. 2

Воздействия и сигналы. 4

Классификация САУ. 5

Математические модели динамических систем. 7

Линеаризация. 8

Линейные динамические системы. 9

Передаточная функция системы. 11

Операторная форма записи передаточной функции. 11

Стандартная форма записи передаточной функции. 12

Передаточная функция в форме изображений по Лапласу. 13

Частотная форма записи передаточной функции. 15

Входные воздействия. 15

Сведение входных воздействий к типовым. 19

Структурные схемы и их преобразования. 20

Математическое описание объектов или систем с помощью графов. 20

Математическое описание дискретных динамических систем или элементов. 24

Описание дискретных систем с помощью дискретных передаточных функций. 31

Передаточная функция дискретной системы. 32

Математическое описание многомерных объектов или систем. 35

Передаточная функция многомерной системы. 37

Анализ систем автоматического управления. 38

Анализ устойчивости. 38

Анализ качества. 40

Косвенные оценки качества. 41

Математическое описание стохастических систем. 42

Свойства функции распределения вероятности: 43

Плотность распределения вероятности. 44

Свойства функции и плотности распределения вероятности многомерной случайной величины. 46

Числовые характеристики случайной величины. 47

Числовые характеристики для случайных функций или процессов. 49

Стационарные случайные функции или процессы. 50

Эргодические случайные функции или процессы. 50

Прохождение случайного сигнала через линейную непрерывную систему. 50

ЛЕКЦИЯ 1.

СИСТЕМА. ЭЛЕМЕНТЫ СИСТЕМЫ.

Цель.  Изучение систем и элементов систем.

Задачи:

1.  Изучить способы математического описания систем управления;

2.  Изучить классификацию систем управления;

3.  Изучить виды воздействий на системы.

Система – это совокупность элементов, взаимодействующих между собой и, обладающие свойствами, отличными от свойств элементов.

Система автоматического управления – это совокупность объекта управления и устройства управления.

Объект управления (ОУ) – это устройство, требуемый режим работы которого должен поддерживаться извне с помощью некоторых управляющих воздействий.

Устройство управления (УУ) – это устройство, поддерживающее требуемый режим работы объекта управления.

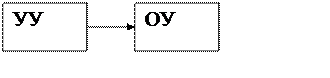
При математическом описании систем используется 2 возможных вида рассмотрения систем:

1. Анализ системы – то есть определение свойств спроектированной системы.

2. Синтез системы – это проектирование системы по заданным свойствам.

Способы математического описания систем.

1. Классический.

В этом случае составляются математические модели отдельных элементов системы и не учитываются взаимосвязи между этими элементами.

2. Системный.

Математическая модель системы представляет собой совокупность математических моделей или математических описаний элементов и математических описаний и моделей связей между элементами.

Математической моделью системы является набор дифференциальных, интегральных, алгебраических и конечно-разностных уравнений.

Описание динамических систем производится с помощью дифференциальных уравнений.

При описании системы с сосредоточенными параметрами используют обыкновенные дифференциальные уравнения, а системы с распределенными параметрами – дифференциальные уравнения с частными производными.

При математическом описании процессов различной физической природы могут использоваться одни и те же уравнения.

Рассмотрим математическое описание двух различных процессов.

1. Колебание маятника.

Процесс колебания маятника можно описать с помощью дифференциального уравнения 2 порядка:

 

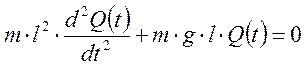
2. Электрический колебательный контур.

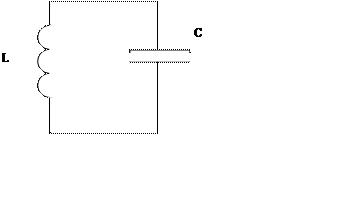
Процессы, происходящие в контуре можно описать с помощью дифференциального уравнения второго порядка:

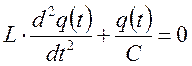
Введем обозначения. Обозначим через:

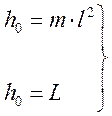 - коэффициент при 2 производной

 - коэффициент при 1 производной

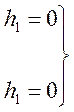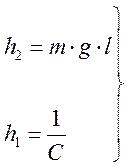- коэффициент при самой функции

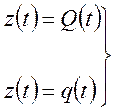 - изменяемая величина.

В результате и для первой и второй системы получим следующее дифференциальное уравнение.

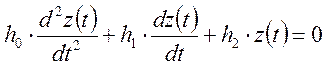
В том случае если на систему извне подается некоторое воздействие x(t), то уравнение примет вид:

Воздействия и сигналы.

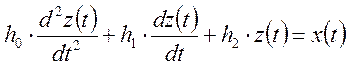
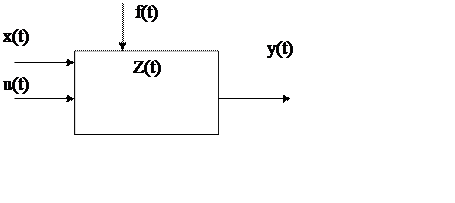
Рассмотрим некоторую систему и воздействие, оказываемое на нее. Воздействия являются переменными системы. Состояние системы в любой момент времени можно описать с помощью следующих воздействий:

- задающее воздействие x(t) – это планируемое воздействие на систему.

- управляющее воздействие u(t) – воздействие устройства управления на объект управления.

- возмущающее воздействие f(t) – это не планируемое воздействие на систему или элемент.

- выходной сигнал y(t) – это величина, характеризующая состояние объекта управления.

- внутреннее состояние системы z(t) – это воздействие одной системы на другую.

Классификация САУ.

Все САУ можно разделить на:

1. линейные и нелинейные.

Линейные системы – это системы, которые можно описать с помощью линейных уравнений.

Нелинейные системы – это системы, которые можно описать с помощью нелинейных уравнений.

2. непрерывные и дискретные.

Непрерывные системы – это системы, состояние которых задано на непрерывном множестве. Эти системы описываются с помощью алгебраических, дифференциальных, интегральных уравнений.

Для дискретных систем характерно наличие дискретных или импульсных элементов. При математическом описании таких систем используются конечно-разностные уравнения.

3. стационарные и нестационарные.

Стационарные системы описываются с помощью уравнений с постоянными коэффициентами.

4. с распределенными и с сосредоточенными параметрами.

Для описания систем с сосредоточенными параметрами используются обыкновенные дифференциальные уравнения; с распределенными – дифференциальные уравнения с частными производными.

5.  детерминированные и стохастические.

Детерминированные системы – это системы, в которых отсутствуют случайные воздействия, и в этом случае в каждый момент времени есть только одно значение выходной величины; в стохастических системах, то есть в системах с наличием случайных воздействий выходная величина в каждый момент времени может принимать несколько различных значений.

6. статические и динамические.

Статические системы описываются однородными уравнениями, а динамические – неоднородными.