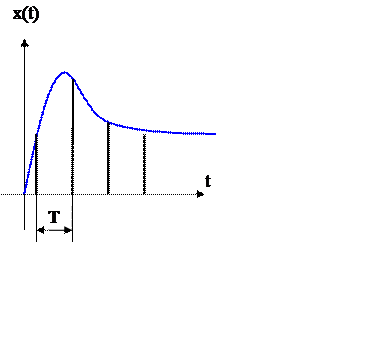
Импульсный
элемент, осуществляющий модуляцию δ импульсами, называется идеальным импульсным
элементом. Идеальные импульсы – это импульсы бесконечно малой длительности,
бесконечно большой амплитуды, площади которых совпадают со значениями
непрерывной функции ![]() .
.
При математическом описании реального импульсного элемента, его представляют в виде идеального импульсного элемента и формирователя импульсов.

Формирователь импульсов преобразует идеальный импульс в импульс заданной формы и, является непрерывным элементом, который можно объединить с непрерывной частью. В результате получим приведенную непрерывную часть. Для упрощения математического описания импульсных систем, включающих в себя как импульсные, так и непрерывные элементы, все непрерывные сигналы представляются в виде фиктивных импульсных сигналов. В этом случае дифференциальные уравнения, используемые для описания непрерывных систем, заменяются разностными уравнениями. Непрерывные преобразования Лапласа заменяются дискретными преобразованиями Лапласа. Возможность такой замены основана на том, что выходной сигнал импульсного элемента определяется значениями непрерывного входного сигнала в дискретные моменты времени, соответствующие началу периода следования импульсов. Следовательно, в работе импульсного элемента ничего не изменится, если заменить входной непрерывный сигнал x(t), сигналом, определенным в моменты времени (nТ). В результате получим дискретный сигнал x(nТ), который совпадает со значением сигнала x(t) в моменты времени (nТ), и равный 0 в остальные моменты времени. Функция x(nt), описывающая такой сигнал называется решетчатой функцией, и исходный непрерывный сигнал будет являться огибающей для решетчатой функции.
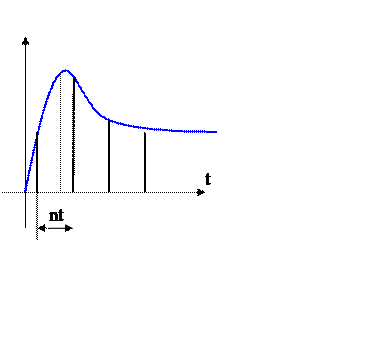
Функция
![]() называется смещенной решетчатой
функцией и определяет поведение непрерывной функции внутри периода.
называется смещенной решетчатой
функцией и определяет поведение непрерывной функции внутри периода.
При описании дискретных систем скорость изменения решетчатой функции будет характеризоваться ее разностью производных более высоких порядков, которые заменяются разностями соответствующего порядка.
Разность 1 порядка в некоторой точке n определяется так:
![]()
Разность 2 порядка определяется так:
![]()
ля k-го порядка:
![]()
Тогда дискретную систему можно описать конечно-разностными уравнениями, определяющими соотношение между выходной функцией y(n), ее разностью и входной функцией x(n) и ее разностями.
![]()
Решение конечно-разностного уравнения [1] можно представить в виде общего решения однородного уравнения и частного решения неоднородного уравнения.
![]() .
.
![]()
Для
решения этого уравнения необходимо задать начальные условия ![]() Линейные дискретные системы
описываются с помощью линейного уравнения [1], а нелинейные с помощью
нелинейного уравнения [1].
Линейные дискретные системы
описываются с помощью линейного уравнения [1], а нелинейные с помощью
нелинейного уравнения [1].
Для получения дискретных передаточных функций используются дискретные преобразования Лапласа и z-преобразования. При таком преобразовании исходная решетчатая функция x(nТ), рассматривается в виде произведения последовательности импульсов единичной площади на исходную непрерывную функцию x(t). Если импульсный элемент является идеальным, то есть время импульса значительно меньше периода, то импульсы единичной площади можно представить в виде δ импульсов и тогда:
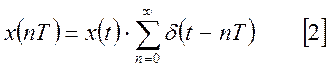
Эти δ
импульсы определены в моменты времени, совпадающие с началом периода. Входная
функция x(t) определена в моменты времени nT. Обозначим решетчатую исходную функцию ![]() , а через
, а через ![]() будем
обозначать непрерывную функцию, определенную в момент времени nT.
будем
обозначать непрерывную функцию, определенную в момент времени nT.
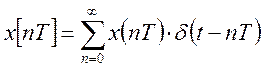
Определим
решетчатую функцию в некоторый фиксированный момент времени ![]() и найдем изображение по Лапласу.
и найдем изображение по Лапласу.
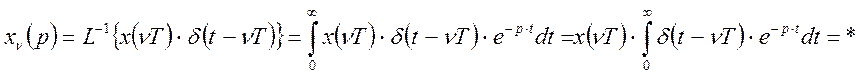
Используя свойства свертки функции:
![]()
Тогда для последовательности импульсов получим:
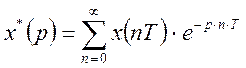
Введем замену переменной:
![]()
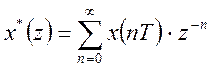 - z-преобразование.
- z-преобразование.
Для смещенной решетчатой функции используется модифицированное z-преобразование.
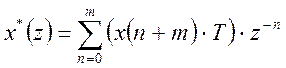
Рассмотрим
некоторую разомкнутую дискретную систему, содержащую идеальный импульсный
элемент и приведенную непрерывную часть, весовая функция которой определяется
как ![]() . Ей соответствует решетчатая весовая
функция
. Ей соответствует решетчатая весовая
функция ![]() .
.

Сигнал, поступающий с идеального импульсного элемента на приведенную непрерывную часть можно представить в виде последовательностей δ импульсов.
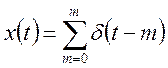
Реакция, приведенная непрерывной
частью на 1 импульс в момент времени t=m, будет определяться произведением ![]() . Тогда реакция на последовательность
импульсов будет представлять собой линейную комбинацию таких произведений.
. Тогда реакция на последовательность
импульсов будет представлять собой линейную комбинацию таких произведений.
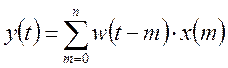
Воспользуемся z-преобразованием:
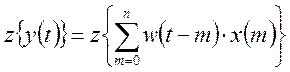
Используя теорему свертки, и переходя к решетчатой функции, получим:
![]()
Обозначим z-преобразование от весовой функции
через ![]() .
.
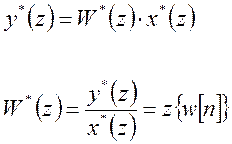
Передаточная функция дискретной замкнутой системы:
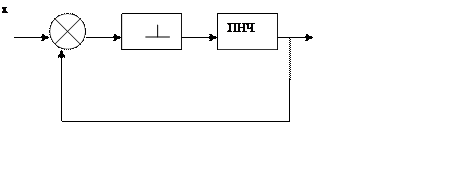
Она определяется как:
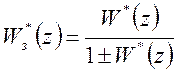
Определим передаточную
функцию дискретной системы. Импульсный элемент, который формирует импульсы
конечной длительности tи, и амплитуды ![]() .
.
Такой импульс можно представить в виде 2 ступенчатых воздействий:
![]()
Весовая функция в таком случае будет определяться так:
![]() ,
,
тогда сигнал на выходе приведенной непрерывной части в любой момент времени t=m будет определяться:
При подаче 1 импульса: ![]()
При последовательности
импульсов: 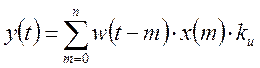
z-преобразование данного выражения будет иметь вид:
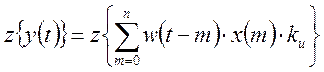
Используя теорему свертки, и переходя к решетчатой функции, получим:
![]()
Обозначим ![]() через
через ![]() .
.
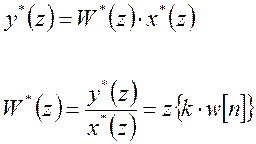
Вопросы для самоконтроля.
1. Идеальные и реальные импульсные элементы.
2. Квантование по времени.
3. Квантование по уровню.
4. Квантование по времени и уровню.
5. Способы модуляции.
6. Структурная схема использования ЭВМ в САУ.
7. Понятие решетчатой функции и дискретного преобразования Лапласа.
8. Передаточная функция дискретных систем.
Лекция 6
Цель. Изучить математическое описание многомерных объектов и систем управления.
Задачи:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.