Система. Элементы системы. Математические модели динамических систем. Входные воздействия. Математическое описание объектов или систем с помощью графов. Математическое описание многомерных объектов или систем, страница 8

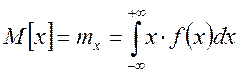
Дискретная случайная величина:

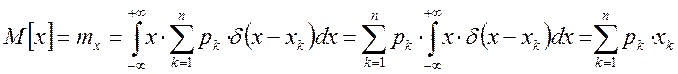
Пусть случайная величина «у» является неслучайной функцией φ случайного аргумента «х». Тогда:

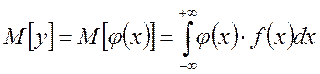
в том случае, если «у» - дискретная случайная величина, то:

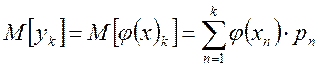
Дисперсия.

Дисперсия характеризует величину разброса случайных значений вокруг математического ожидания.

Непрерывная случайная величина:

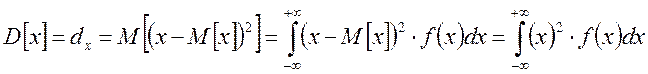
Дискретная случайная величина:

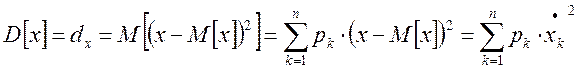
Корреляционная функция.

Корреляционная функция определяет связь между случайными функциями или случайными величинами.

Рассмотрим 2 случайных величины x_i и x_j.

Тогда корреляционная функция будет определяться так:

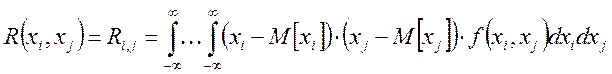
Свойства корреляционной функции:

1.

2.

3. Если случайные величины x_i и x_j независимы, то корреляционная функция равна 0.

В том случае, если корреляционная функция определяется для многомерной случайной величины, то она будет иметь вид матрицы:

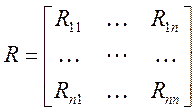
Эта матрица называется корреляционной матрицей.

Величина, определяемая как:

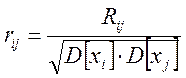
называется коэффициентом корреляции.

Свойства коэффициента корреляции:

1.

2.

3. .

4. Если величины x_i и x_j независимы, то коэффициент корреляции равен 0.

Числовые характеристики для случайных функций или процессов.

Рассмотрим некоторую непрерывную случайную функцию x(t).

Математическое ожидание случайной функции имеет вид:

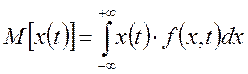
Дисперсия случайного процесса – это величина, определяемая как:

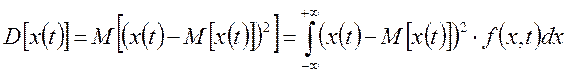
Корреляционная функция случайного процесса:

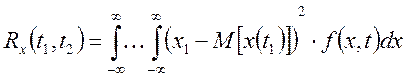
Взаимная корреляционная функция определяется:

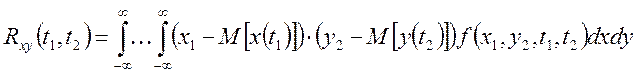
Корреляционная функция некоторого случайного процесса характеризует взаимосвязь значений случайных функций в моменты времени  .

Взаимная корреляционная функция характеризует взаимосвязь между случайными функциями или процессами Х и У в моменты времени  .

Вопросы для самоконтроля.

1.  Плотность и функция распределения вероятности для непрерывных случайных величин.

2.  Плотность и функция распределения вероятности для многомерных и дискретных случайных величин.

3.  Свойства функции плотности распределения.

4.  Числовые характеристики случайных величин.

5.  Числовые характеристики случайных процессов.

ЛЕКЦИЯ 9.

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ ИЛИ ПРОЦЕССЫ.

Цель. Изучение стационарных и эргодических  случайных процессов

Задачи:

1.  Изучить характеристики стационарных случайных процессов

2.  Изучить характеристики эргодических  случайных процессов

3.  Изучить прохождение случайного сигнала через непрерывную систему.

Случайные функции, для которых все n-мерные функции распределения вероятностей не изменяются в зависимости от начала отсчета времени, то есть выполняется равенство:

называются стационарными в узком смысле.

Аналогичное равенство справедливо и для плотности распределения вероятностей:

Для непрерывной величины случайная функция с постоянным математическим ожиданием и корреляционной функцией, не зависящей от момента времени t₁ и t₂, а зависящей только от разности аргументов, то есть выполняется равенство:

 

называется стационарной функцией в широком смысле.

Для дискретной величины должно выполняться условие:

Две случайные функции x(t) и y(t) называются стационарно связанными, если их взаимная корреляционная функция не зависит от аргументов, а зависит только от их разности.

Для стационарных процессов справедливо равенство:

Для двух дискретных процессов «х» и «у» для их стационарности должно выполняться равенство:

Эргодические случайные функции или процессы.

Стационарный процесс, для которого статистические характеристики, полученные усреднениями одной реализации на достаточно длительном промежутке времени, совпадают с достаточной степенью точности с усреднением множества реализации в фиксированный момент времени, называются эргодическими.

Случайная функция называется эргодической по отношению к математическому ожиданию, если выполняется условие:

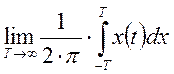 - усреднение одной реализации и совпадает с усреднением по множеству реализаций:

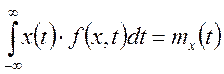
Случайная функция называется эргодической по отношению к дисперсии, если выполняется равенство:

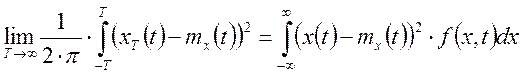
 - одна реализация,

 - множество реализаций.

Случайный процесс называется эргодическим по отношению к корреляционной функции, если выполняется равенство:

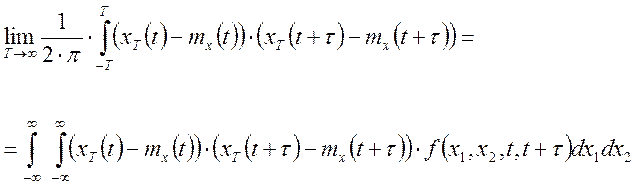
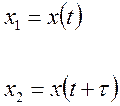
Для дискретных случайных процессов, эргодичных по отношению математическому ожиданию, справедливо следующее равенство:

 

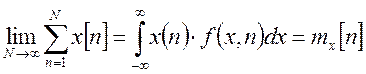
Дискретная случайная функция называется эргодической по отношению к дисперсии, если выполняется равенство:

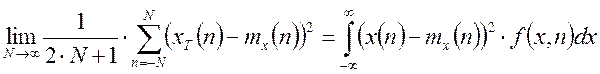
Некоторый дискретный случайный процесс называется эргодическим по отношению к корреляционной функции, если выполняется равенство:

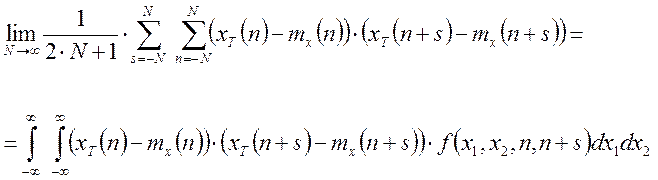
Прохождение случайного сигнала через линейную непрерывную систему.

Рассмотрим систему, на которую действует случайный сигнал . Весовая функция этой системы или элемента  , тогда случайный выходной сигнал  можно определить:

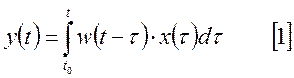
Если для входного случайного сигнала заданы математическое ожидание и корреляционная функция, то можно определить числовые характеристики выходного сигнала:

1. Математическое ожидание выходного сигнала:

Применим операцию математического ожидания для левой и правой части [1].

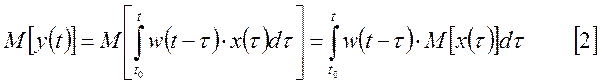
2. Определим корреляционную функцию выходного сигнала. Для этого из [1] вычтем [2].

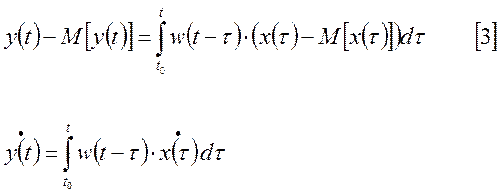
Запишем полученное выражение для момента времени t₁ и t₂,

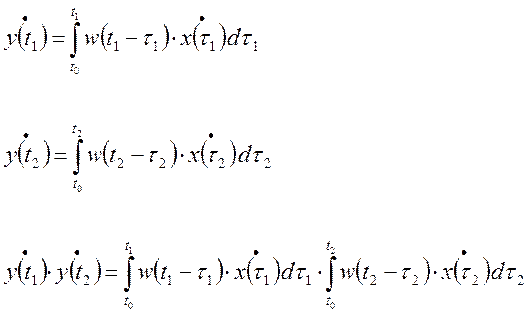
Применим к левой и правой части операцию математического ожидания.

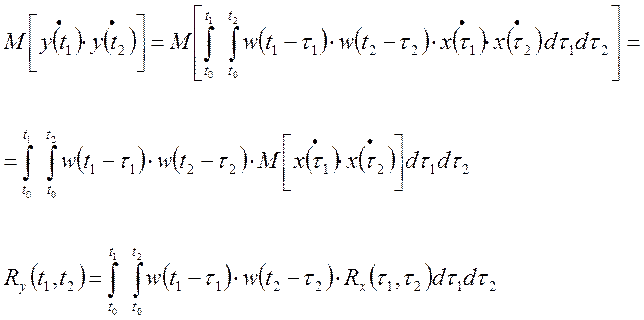
Дисперсия выходного сигнала:

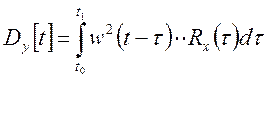
4. Взаимная корреляционная функция:

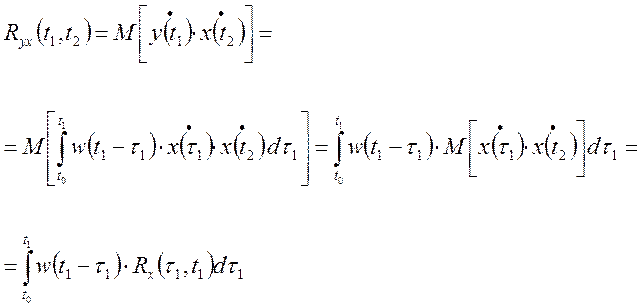
 определяется аналогично.

Вопросы для самоконтроля.

1.  Понятие стационарности в узком смысле.

2.  Понятие стационарности в широком смысле.

3.  Условие эргодичности процесса по отношению к математическому ожиданию.

4.  Условие эргодичности процесса по отношению к дисперсии.

5.  Условие эргодичности процесса по отношению к корреляционной функции.

6.  Вывод взаимной корреляционной функции.