Синтез систем автоматического регулирования: Методические указания к выполнению курсовой работы, страница 8

Для упрощения дальнейших исследований и более наглядного восприятия задачи необходимо составить структурную схему системы управления с неопределенным пока регулятором. Для этого отдельные функциональные элементы объекта, с учетом выделенных измеряемых переменных, надо записать в форме «вход-выход», после чего, используя аппарат передаточных функций, легко установить операторную связь между интересующими нас переменными системы. При этом неизвестный на данном этапе регулятор можно изобразить на структурной схеме в виде прямоугольника, для которого входными воздействиями являются измеряемые переменные, а выходом - управляющее воздействие на объект.

Отметим, что в соответствии с техническим заданием задача синтеза регулятора должна быть решена в двух постановках - в непрерывной и в дискретной. В связи с этим, наряду с дифференциальной моделью непрерывного объекта, необходимо иметь дискретную модель, представленную разностными уравнениями, или структурную схему эквивалентной дискретной системы, построенную с использованием z-передаточных функций, причем для дальнейших исследований в рамках данной курсовой работы последний вариант является более предпочтительным.

При нахождении дискретной модели в виде разностных уравнений удобно использовать форму Коши. В этом случае матрицы дискретной модели определяются ( аналитически или численно) по известным соотношениям, связывающим матрицы непрерывной модели и ее дискретного аналога. При составлении структурной схемы дискретной системы может быть использован тот же подход, что и в непрерывном случае. Однако более удобным является непосредственное использование для этой цели структурной схемы исходной непрерывной системы, в которой в качестве регулятора используется БЦВМ. В этом случае следует учитывать некоторые особенности операторного дискретного представления такой системы, связанные с наличием в ней одного импульсивного элемента (экстраполятор нулевого порядка на выходе регулятора) и нескольких квантующих элементов (АЦП для каждой измеряемой переменной на входе регулятора).

2. Исследование возможности решения задачи с помощью простейшего (статического) регулятора.

На этом этапе курсовой работы исследуется один из наиболее простых подходов в практике автоматического регулирования, который известен как метод параметрического синтеза.

Этот метод состоит в следующем: задается структура регулятора, например, из условия простоты или удобства его реализации, после чего параметры этого регулятора подбираются так, чтобы удовлетворить заданным требованиям к качеству регулирования.

На данном этапе курсовой работы за основу рекомендуется принять статический регулятор, как наиболее простой с точки зрения реализации. Уравнения такого регулятора имеют вид , где y₁, y₂ – измеряемые переменные, а k₁, k₂ – искомые коэффициенты передачи. Для определения параметров k₁ и k₂  можно использовать метод построения областей в плоскости этих параметров, в которых удовлетворяются те или иные требования. При этом в первую очередь необходимо построить область, в которой замкнутая система асимптотически устойчива. Для этого следует определить характеристический полином замкнутой системы D(s), коэффициенты которого будут выражены через неизвестные параметры k₁ и k₂ , после чего, используя критерий Гурвица или Михайлова, можно записать условия устойчивости, которые и определят искомую область. При составлении условий устойчивости следует помнить, что по каждой измеряемой переменной должна осуществляться отрицательная обратная связь. Далее могут быть определены условия, при которых выполняются требования к точности стабилизации (слежения) и требования к быстродействию. Соответствующие этим условиям множества значений параметров k₁ и k₂ определяют области требуемой точности и требуемого быстродействия.

При определении условий требуемой точности в задачах стабилизации при ступенчатом внешнем возмущении (варианты 1, 2, 3, 5) целесообразно воспользоваться теоремой о предельных значениях, выражающей одно из свойств преобразования Лапласа (для непрерывной системы) или z-преобразования (в случае использования в качестве регулятора БЦВМ). В задаче слежения (вариант 4) задающее воздействие принадлежит к классу неопределенных и задается значениями максимальной скорости () и максимального ускорения (). В связи с этим при определении условий точности в этом варианте следует воспользоваться методом эквивалентного гармонического воздействия, параметры которого могут быть определены по заданным значениям  и .

Для определения условий и построения области требуемого быстродействия можно воспользоваться понятием степени устойчивости h. Этот параметр определяется абсолютной величиной вещественной части ближайшего к мнимой оси корня характеристического полинома устойчивой замкнутой системы и связан со временем регулирования приближенным соотношением . Если определить таким образом желаемое значение h* и формально записать условия устойчивости для характеристического полинома 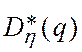, где  - новая комплексная переменная, то полученная область в плоскости параметров k₁, k₂ будет являться искомой областью требуемого быстродействия. При этом значения k₁, k₂ на границе области будут соответствовать желаемому быстродействию, а значения этих параметров внутри области определят более быстрый переходной процесс.

Отметим, что выбранный за основу статический регулятор, вообще говоря, не гарантирует существования решения задачи в смысле удовлетворения требованиям технического задания. В частности, может оказаться, что условия устойчивости и точности являются несовместными. В этом случае дальнейшие исследования на данном этапе не имеют смысла.