Построение амплитудно-фазовой характеристики системы автоматического регулирования скорости двигателя постоянного тока

Задача №1

Дана система автоматического регулирования скорости двигателя постоянного тока, с гибкой обратной связью.

1.  Построить амплитудно-фазовую характеристику (АФХ) и её ЛАЧХ.

С_е=0,02; К_q=0,6;

J_р=140; К₀=0,4;

Т_м=0,7; К_с=0,6;

Т₀=0,009; К_у=110;

Т_q=0,04; К_u=1.

Структурная схема системы автоматического регулирования скорости двигателя постоянного тока с гибкой обратной связью имеет вид:

 

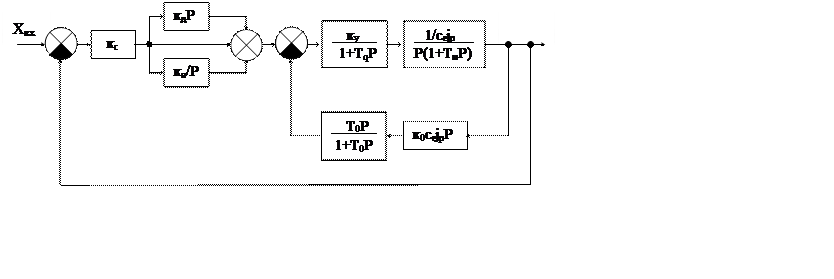Рис. 1

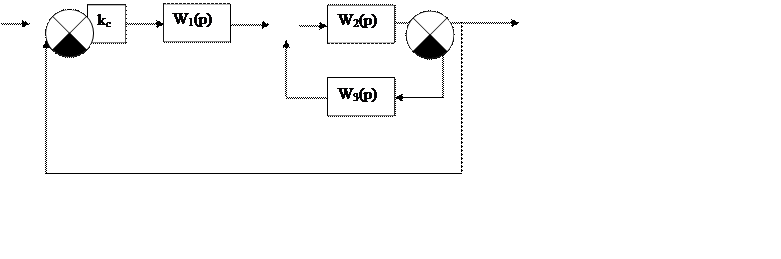
Используя правила эквивалентных преобразований упростим структурную схему и определим передаточные функции замкнутой и разомкнутой системы:

 

 

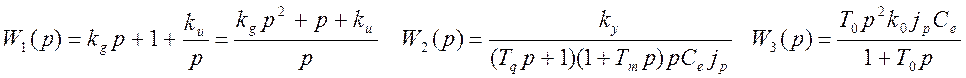
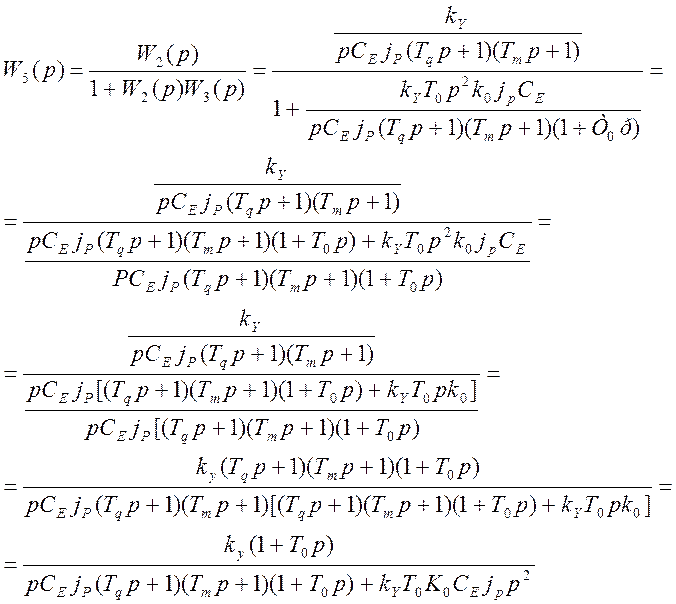
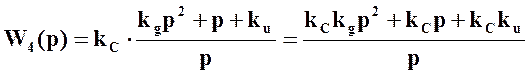
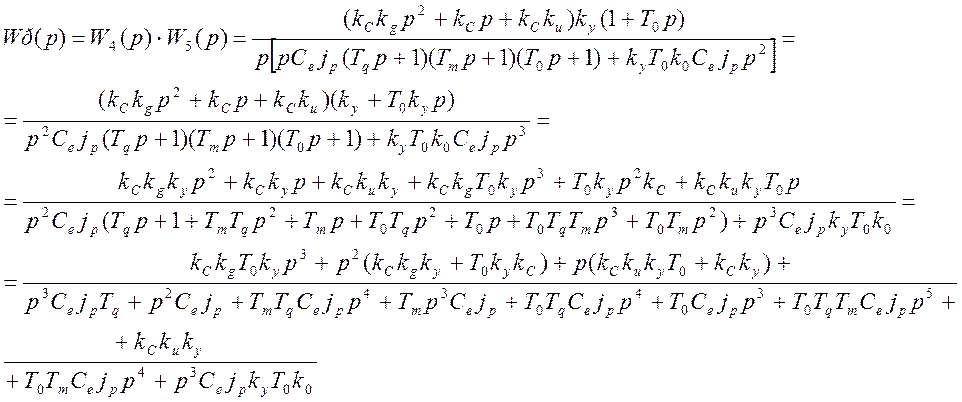
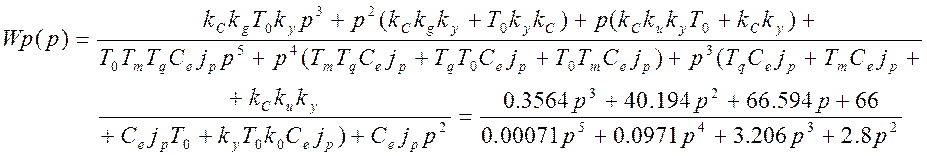
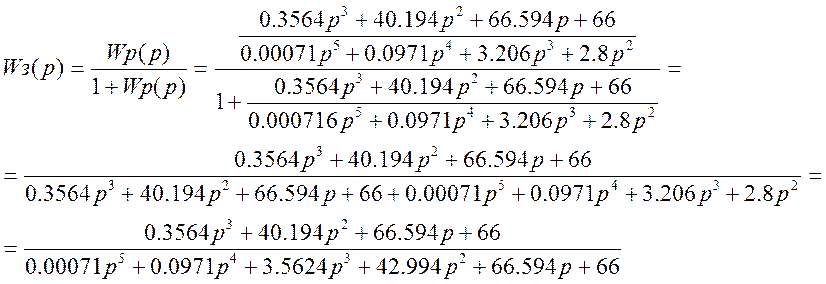
Запишем частотную передаточную функцию (p®jw)

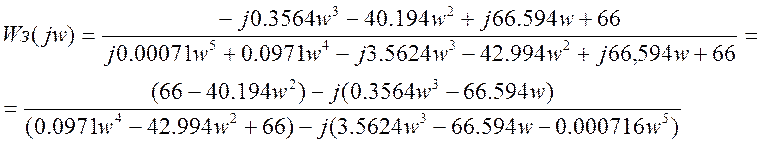
Умножим числитель и знаменатель частотной передаточной функции замкнутой системы на комплексно-сопряженное значения знаменателя этой функции, т.е. на , и выделим действительную и мнимую части из полученной функции:

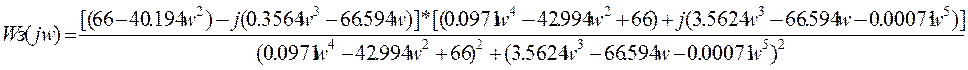
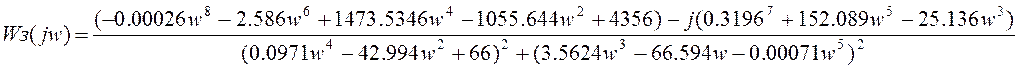
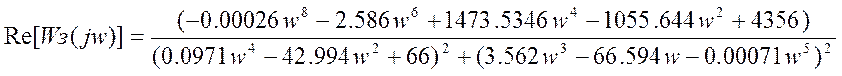
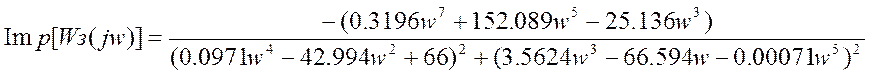
Имея значения re и imp, строим АФХ замкнутой системы при w, изменяющейся от 0 до ¥:

Таблица №1

ω	Re	Im	ω	Re	Im
0,1	1,00041	0,00001	7	0,83559	-0,73744
0,5	1,01213	-0,00039	7,1	0,82967	-0,74653
0,8	1,03616	-0,00896	7,4	0,81170	-0,77354
0,9	1,04695	-0,01679	7,5	0,80565	-0,78245
1	1,05813	-0,02823	7,8	0,78728	-0,80890
1,1	1,06870	-0,04333	7,9	0,78110	-0,81762
1,4	1,08866	-0,10331	8	0,77489	-0,82629
1,5	1,09052	-0,12463	8,1	0,76865	-0,83491
1,6	1,09040	-0,14520	8,4	0,74979	-0,86046
1,9	1,08258	-0,19979	8,5	0,74346	-0,86888
2	1,07866	-0,21563	8,6	0,73711	-0,87724
2,1	1,07447	-0,23051	8,9	0,71793	-0,90202
2,4	1,06130	-0,27083	9	0,71151	-0,91017
2,5	1,05688	-0,28322	9,1	0,70507	-0,91826
2,6	1,05249	-0,29524	9,2	0,69862	-0,92630
2,9	1,03947	-0,32969	9,5	0,67919	-0,95009
3	1,03517	-0,34078	9,6	0,67269	-0,95791
3,1	1,03088	-0,35173	9,9	0,65316	-0,98102
3,4	1,01800	-0,38391	10	0,64664	-0,98860
3,5	1,01369	-0,39447	13	0,45395	-1,18810
3,6	1,00935	-0,40496	14	0,39333	-1,24209
3,9	0,99617	-0,43608	15	0,33563	-1,28978
4	0,99171	-0,44635	18	0,18371	-1,39644
4,1	0,98721	-0,45659	19	0,14071	-1,42061
4,2	0,98266	-0,46678	20	0,10157	-1,43959
4,5	0,96876	-0,49713	30	-0,11474	-1,42036
4,6	0,96403	-0,50718	40	-0,15317	-1,22050
4,9	0,94954	-0,53711	50	-0,13878	-0,99735
5	0,94461	-0,54702	60	-0,11489	-0,80134
5,1	0,93962	-0,55689	70	-0,09307	-0,64181
5,4	0,92436	-0,58630	80	-0,07545	-0,51559
5,5	0,91917	-0,59604	90	-0,06171	-0,41668
5,8	0,90330	-0,62502	95	-0,05604	-0,37560
6	0,89247	-0,64416	100	-0,05105	-0,33924
6,1	0,88698	-0,65367	250	-0,00837	-0,03583
6,4	0,87024	-0,68196	500	-0,00207	-0,00491
6,5	0,86457	-0,69131	750	-0,00092	-0,00148
6,8	0,84730	-0,71912	1000	-0,00052	-0,00063
6,9	0,84146	-0,72830	10000	-0,00001	0,00000

Диаграмма№1

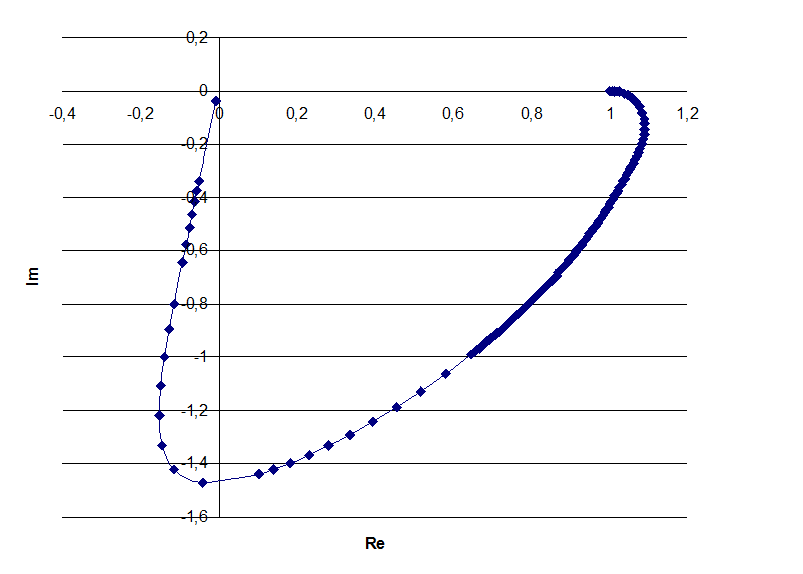
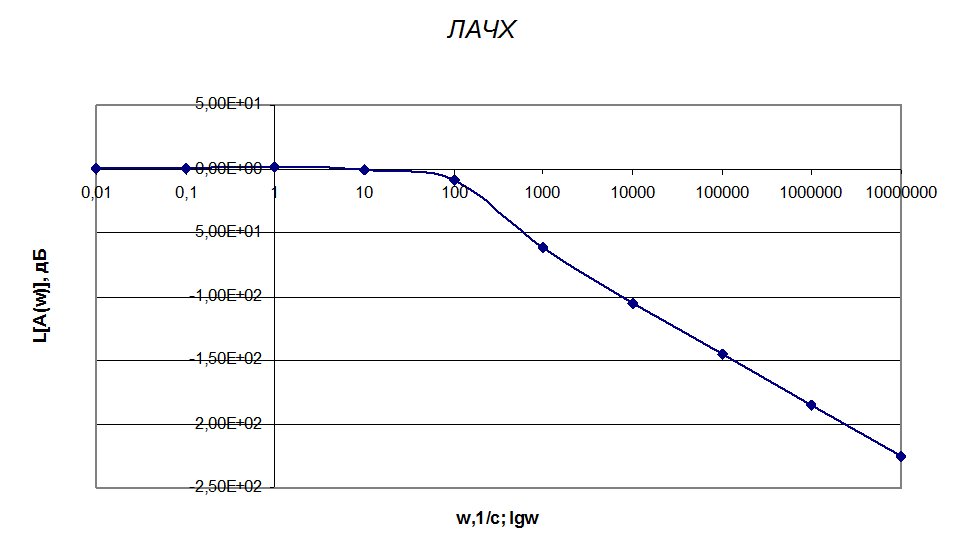
Построим ЛАЧХ замкнутой системы:

L(w)=20lg½A(w)½;         ;

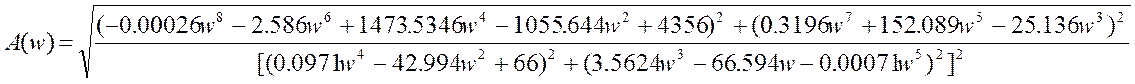
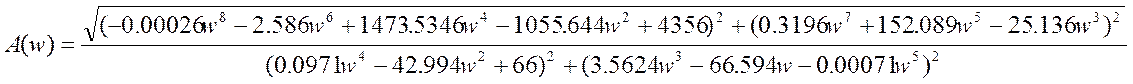
L(w)=20lg-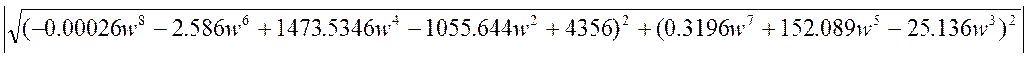

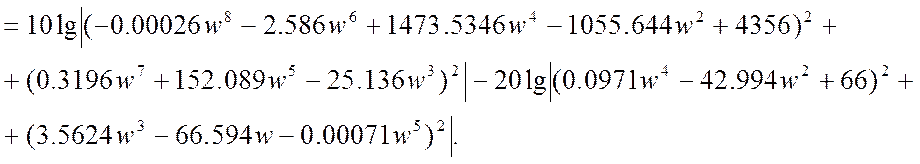-20lg½½=

Таблица №2

W, 1/с	L[A(w)]
0,01	5,41E-04
0,1	5,38E-02
1	2,23E+00
10	-3,87E-02
100	-9,29E+00
1000	-6,18E+01
10000	-1,06E+02
100000	-1,46E+02
1E+06	-1,86E+02
1E+07	-2,26E+02

Диаграмма №2

Выводы:

Вещественная часть АФХ замкнутой системы, полученной в п.1. является четной функцией частоты, так как частота входит как в числитель, так и в знаменатель только в четных степенях и следовательно:

U(w)=U(-w);

Мнимая часть АФХ замкнутой системы является нечетной функцией частоты, так, как w входит в знаменатель при четных степенях, а числитель можно представить как произведение частоты на сомножитель, содержащий w в четных степенях, следовательно:

V(w)=-V(-w);

Таким образом в точке АФХ замкнутой системы соответствующего значению w и –w имеют 1 и ту же абсциссу и равную по модулю, но не равную по знаку ординаты, следовательно эта АФХ симметрична относительно действительной оси и достаточно построить ее только для диапазона частот от 0 до ¥, так как другая ветвь характеристики для w от -¥ до 0 является ее зеркальным отображением построенной части относительно действительной оси.

Полученная ЛАЧХ имеет 2 асимптоты, 1-асимптота представляет собой прямую лежащую на оси частот, а 2-ая асимптота имеет наклон -40дБ/дек. На характеристике имеется 1 частота сопряжения: w₁=100 1/с.

2. Исследуем устойчивость системы по критерию Найквиста и определим запасы устойчивости  по модулю и по фазе.

Согласно критерию устойчивости Найквиста, об устойчивости замкнутой системы можно судить, исследовав устойчивость ее разомкнутой системы. Т.е. если АФХ разомкнутой системы не охватывает на комплексной плоскости точку с координатой (-1; j0), то систему можно считать устойчивой.

Для этого построим АФХ разомкнутой системы:

;

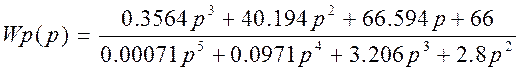Запишем частотную передаточную функцию разомкнутой системы, заменив р→jω:

;

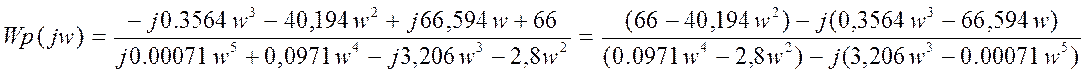
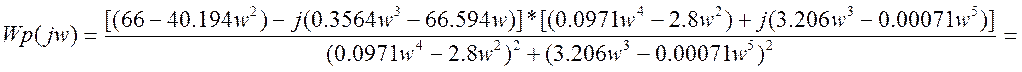
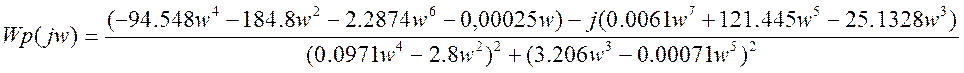
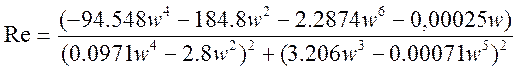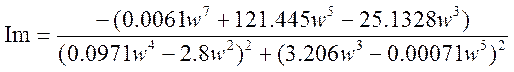
таблица №3