Построение амплитудно-фазовой характеристики системы автоматического регулирования скорости двигателя постоянного тока, страница 2

Диаграмма №3

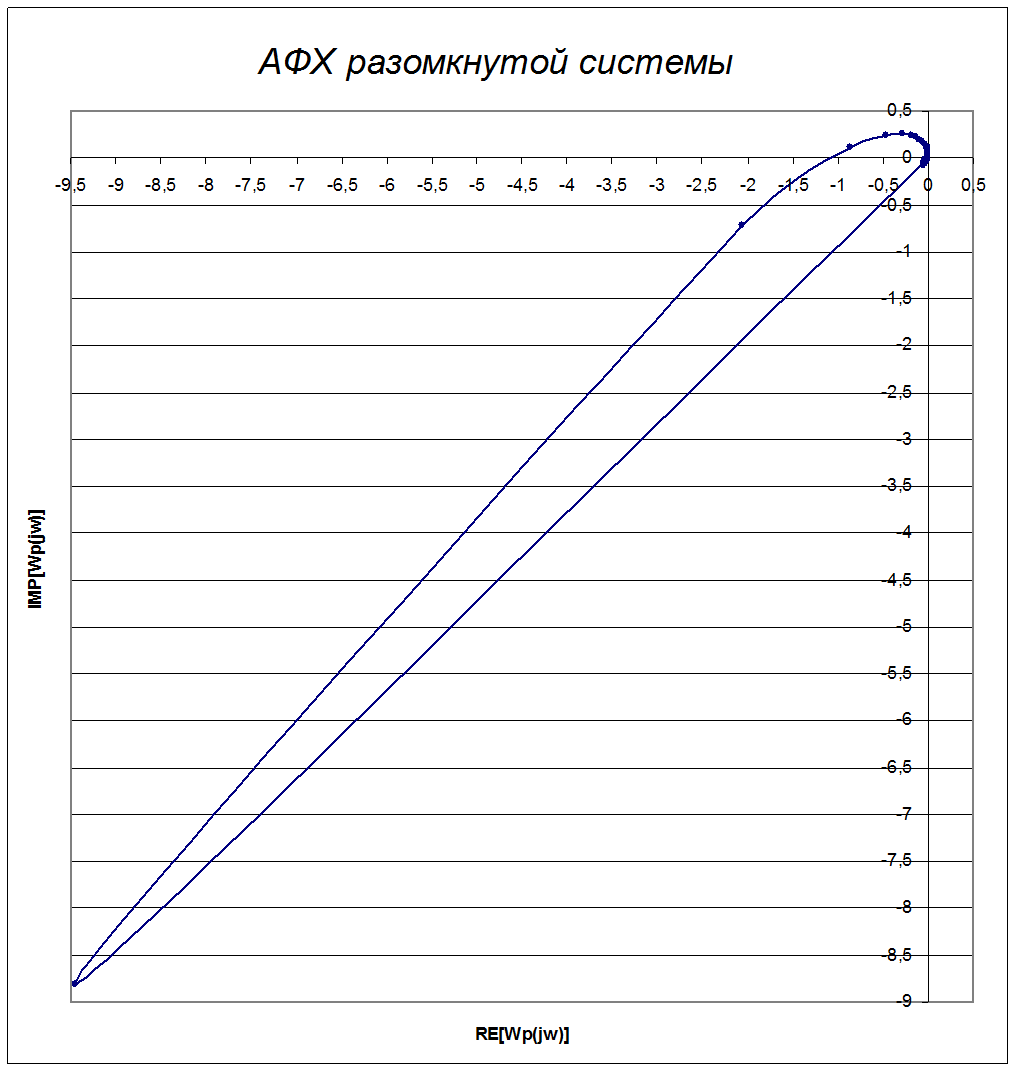
Строим единичную окружность и находим точку пересечения единичной окружности с АФХ:

(Диаграмма №3 в увеличенном масштабе)

а

j

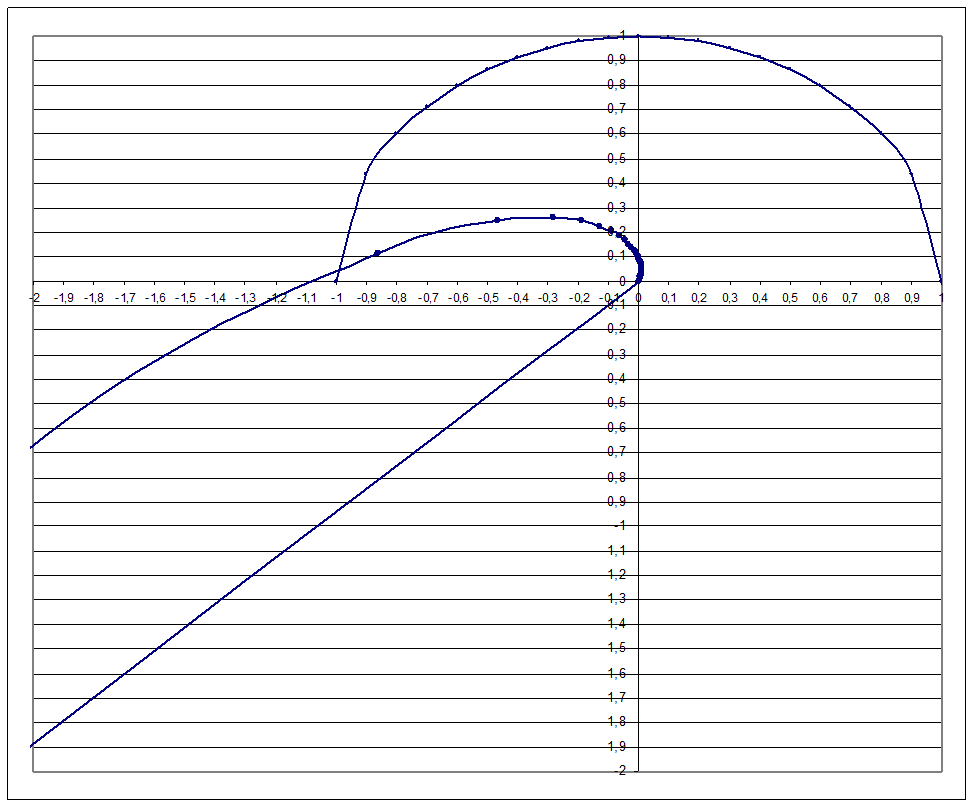
На графике видно, что АФХ разомкнутой системы не пересекает точку с координатой (-1;j0), значит система устойчива по критерию Найквиста.

Сделаем проверку устойчивости этой системы по критерию Гурвица, для этого составляем характеристический полином – знаменатель передаточной функции разомкнутой системы вида  а₀lⁿ+ а₁l^n-1+…+ а_т-1l + а_n = 0, и главный определитель Гурвица из коэффициентов характеристического полинома:

=0

           

 ;          

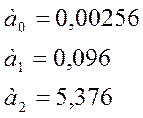
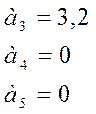
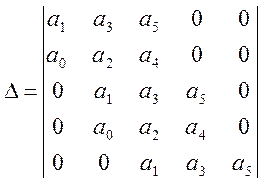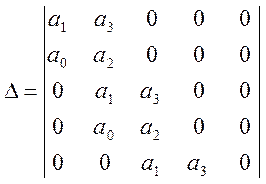
 Главный определитель Гурвица

, ;

,

;

;

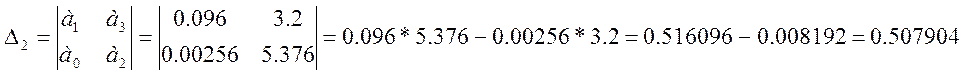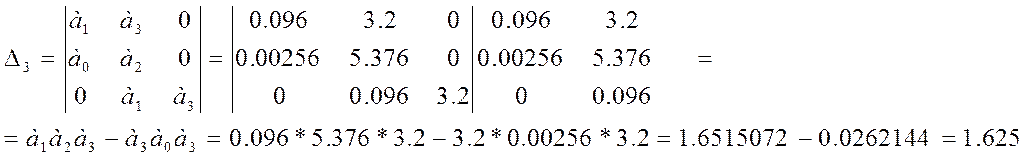
Из вычислений следует, что система является устойчивой, так как при а0>0, главный определитель Гурвица и все его диагональные миноры положительные.

Определим запасы устойчивости по модулю и фазе

·  Запас устойчивости по модулю определяется следующим образом: М=*100%, где в=1, а – точка пересечения АФХ раз. системы с действительной осью, т.е. из рис. на стр. 10 видно, что а=1,1, т.е. М=110%. Для данной системы наблюдается большой запас устойчивости по амплитуде (модулю), т.к. значение 110% превышает норму 15-30%.

·  Запас устойчивости по фазе определяется следующим образом:

Точка пересечения единичной окружности и АФХ раз. системы соединяется с началом координат с помощью прямой. Угол отклонения этой прямой от действительной оси дает нам величину запаса устойчивости по фазе.

Из рис. стр.10 видно, что этот угол j=-3°, что говорит об очень малом запасе устойчивости по фазе в этой системе.

3. Построение переходного процесса системы методом трапеций и исследование его

Пусть замкнутая система имеет вещественную частотную характеристику следующего вида:

U(w)=RE[Wз(w)], U=f(w),

Таблица №5

w	U(w)	3,5	-0,41089	7,5	-0,06161	11,5	-0,0054
0	1	4	-0,35543	8	-0,04902	12	-0,00244
0,5	1,021047	4,5	-0,27064	8,5	-0,03882	12,5	9,56E-05
1	1,115511	5	-0,20568	9	-0,03048	13	0,002261
1,5	1,353744	5,5	-0,15845	9,5	-0,02357	13,5	0,004115
2	1,87098	6	-0,12369	10	-0,01781	14	0,0057
2,5	2,260779	6,5	-0,09753	10,5	-0,01297	14,5	0,007054
3	0,139379	7	-0,0774	11	-0,00887	15	0,008205

Диаграмма №4

 

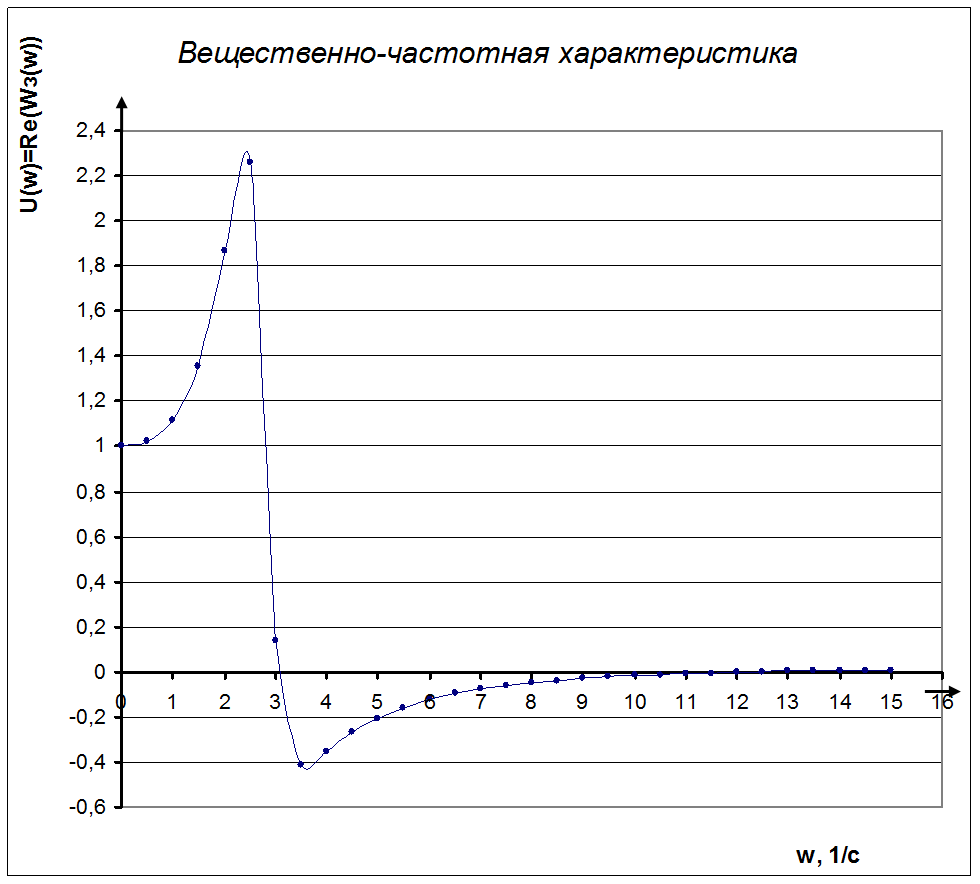
Вещественно-частотную характеристику легко разделяют на небольшое число трапециидальных составляющих (стр.13), расположенных так, что их основания совпадают с осью частот. В данном случае характеристика представлена 5 составляющими: 0лв¢г¢, 0кж¢г¢, 0едм, 0б¢о¢н¢, 0о²рн (0-начало координат).

Для трапеции 1 - 0лв¢г¢:

Uф0₍₁₎= Uф₁- Uф₂=2,3-(-0,4)=2,7;               w_d(1)=w₂=2.5;

w₀₍₁₎=w₃=3.5;                                      c₁=w_d1/w₀₍₁₎=2.5/3.5»0.7;

Для трапеции 2 – 0кж¢г¢:

Uф0₍₂₎=Uф₁₍₂₎-Uф₂₍₂₎=0,15-(-0,4)=0,55;          w_d(2)=3;

w₀₍₂₎=w₃=3.5;                  c₂=w_d(1)/w₀₍₁₎=3/3.5»0.85;

Для трапеции 3 – 0едм:

Uф0₍₃₎=Uф₂=-0,4;           w_d(3)=w₄=3.75;

w₀₍₃₎=w_e=12;                   c₃=w_d(3)/w₀₍₃₎=3.75/12»0.3;

Для трапеции 4 – 0б¢о¢н¢:

Uф0₍₄₎=Uф₃-Uф₁=1,35-2,3=-0,95;                w_d(4)=w₀=1,5;

w₀₍₄₎=w₁=2,25;                c₄=w_d(4)/w₀₍₄₎=1,5/2,25»0.65;

Для трапеции 5 – 0о²рн:

Uф0₍₅₎=Uф₀-Uф₃=1-1,35=-0,35;          w_d(5)=w₀=0,5;

w₀₍₅₎=w₀=1.5;                  c₅=w_d(5)/w₀₍₅₎=0.5/1.5»0.35;

Составим таблицу переходного процесса и по ее данным построим график переходного процесса:

Таблица №6