Построение амплитудно-фазовой характеристики системы автоматического регулирования скорости двигателя постоянного тока, страница 4

Диаграмма №5

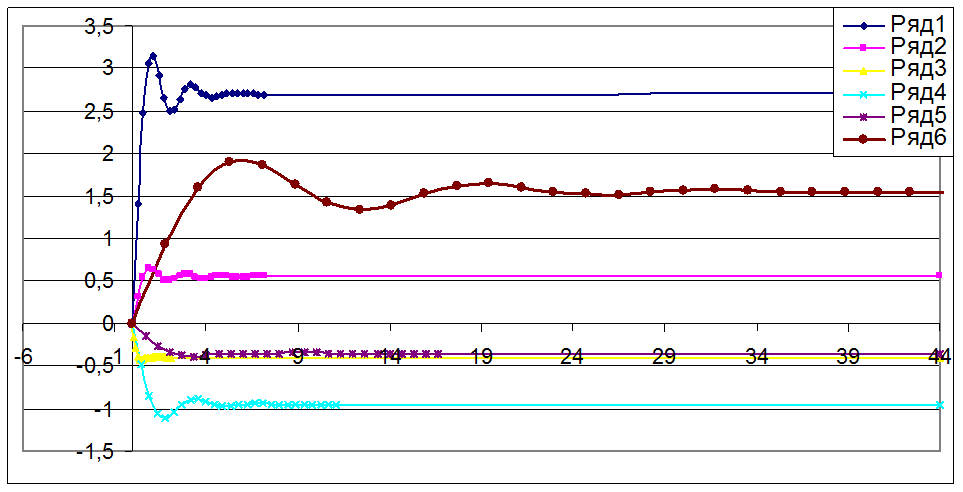
На диаграмме №5 путем суммирования всех функций получаем ряд6 – x_общ(t) – фазовый портрет переходного процесса.

Любая трапециидальная действительная характеристика характеризуется следующими параметрами:

c - коэффициент наклона;

w₀ – полоса пропускания частот;

w_d – полоса равномерного пропускания;          ;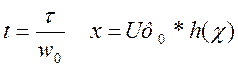

Так как сумма переходных процессов от отдельно составляющих образует переходный процесс системы в целом, то сумма составляющих, имеющих форму трапеций образуют действительную частотную характеристику.
Диаграмма №6

4.  Вычисление интегральной оценки качества заданной системы.

Основными показателями качества нелинейной системы является время  регулирования переходного процесса, перерегулирование и колебательность (амплитуда и частота автоколебаний).

Временем регулирования tp называется время, в течении которого, начиная с момента приложения воздействия на систему, отклонения от значений регулируемой величины Dh(t) от ее установившегося значения будут меньше наперед заданного значения e. Таким образом время регулирования определяет длительность (быстродействие) переходного процесса.

Перерегулированием s называется максимальное отклонение Dh_макс регулируемой величины от установившегося значения h₀, выраженное в % по отношению к h₀.

Колебательность системы характеризуется числом колебаний регулируемой величины за время регулирования tp. Если за это время переходный процесс в системе совершает число колебаний меньше заданного  по условиям технологии, то считается имеет требуемое качество регулирования в части ее колебательности.

В общем случае установившаяся  ошибка  e₀ или точность регулирования определяется как разность 2-х значений – установившейся регулируемой величины после окончания переходного процесса и заданного g₀.

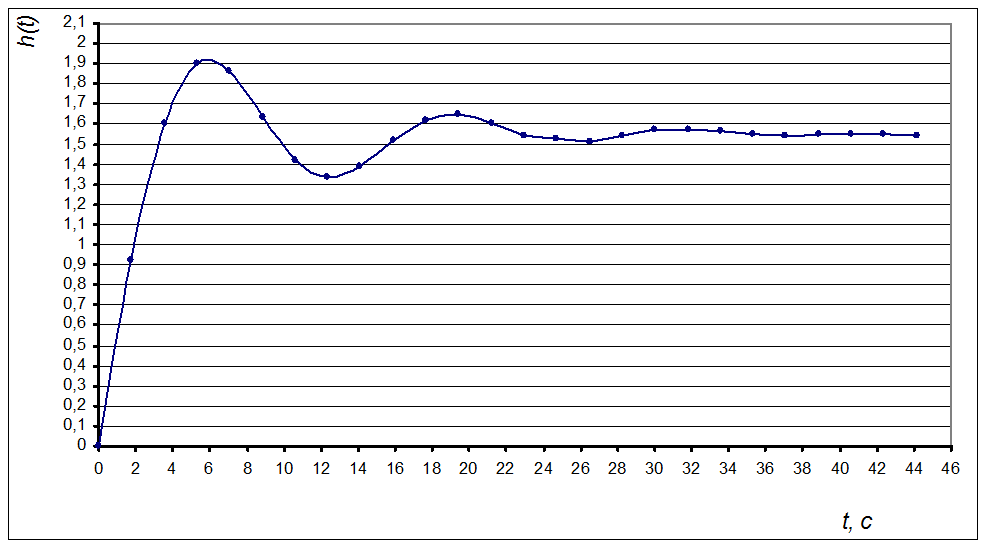
Из диаграммы №6 стр.16 видно, что величина времени регулирования переходного процесса составляет tp=35; период колебаний Т=13,5; время нарастания t_H=3с; ; ; ; ; ;  время достижений 1-го максимума t_макс=6с; точность регулирования (установившаяся ошибка) .

Произведем расчеты оценок качества системы:

·  Перерегулирование рассчитывается по формуле:

;      

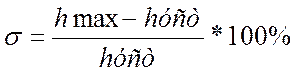·  Декремент затухания ;          ;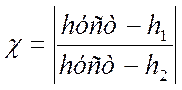

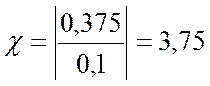·  Определим собственную частоту колебаний по формуле:

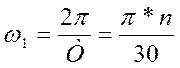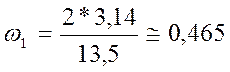;               (с^-1);

·  Коэффициент затухания определяется по формуле:

;            ;

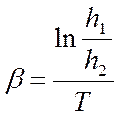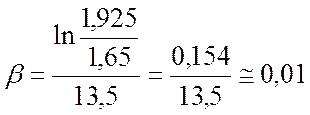·  Определим значение резонансной частоты по формуле:

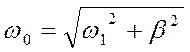
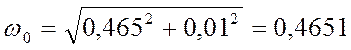             (с^-1)

·  Показатель степени затухания: ;              ;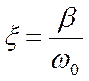

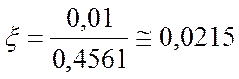·  Колебательность М=3 (число колебаний за время регулирования).

Для уменьшения время регулирования переходного процесса достаточно увеличить коэффициент усиления или декремент затухания. Или для уменьшения перерегулирования  можно уменьшить время нарастания или ввести корректирующие звенья.

 Метод интегральных оценок качества позволяет получить в результате вычислений определенных интегралов от некоторой функции уравнений переменной суммарную ошибку за все время процесса управления. Интегральная оценка качества относится к косвенным оценкам качества систем.

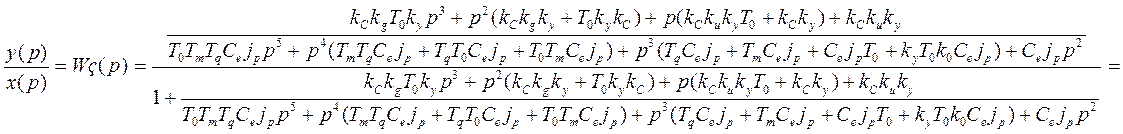
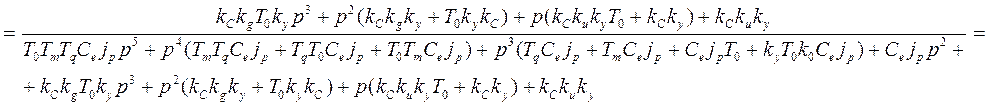
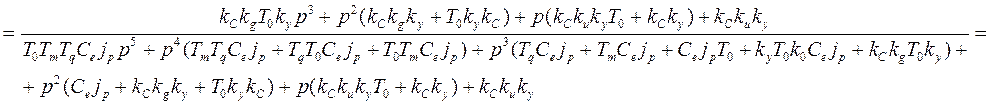y(t)=x0(t)-x(t);       Y(P)=X0(P)-X(P);          X(P)=Wз(P)*L[1(t)]=Wз(P)/P;

X(P)=Wз(0)*L[1(t)]=Wз(0)/P;            Y(P)=(Wз(0)-Wз(P))/P;          Wз(0);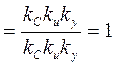

Представим, что полученный переходный процесс имеет линейный характер, тогда линейная интегральная оценка качества системы при поступлении на ее вход единичного ступенчатого управляющего воздействия определяется через значения передаточных функций замкнутой системы для установившегося и неустановившегося ее состояний, т.е. Y1=lim_P®0Y(P), где

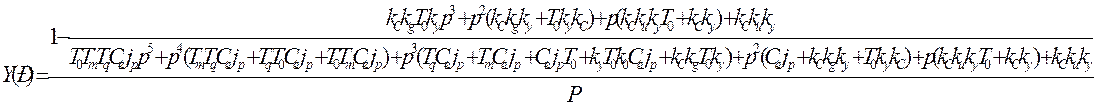
Y(Р)=[]: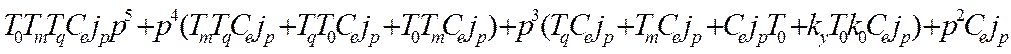

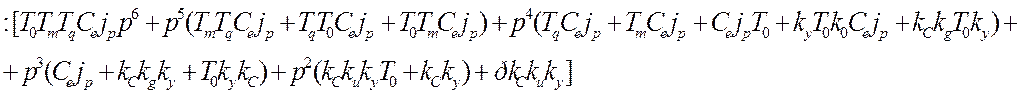
Y1=lim_P®0Y(P)=0/0, имеем неопределенность типа 0/0, используя теорему Лопиталя lim_x®af(x)/g(x)=lim_{x®a a}f¢(x)/g¢(x) получаем неопределенность вида:

Y1=lim_P®0[]:

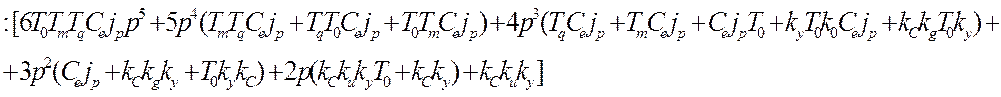
при постановки 0 вместо Р получаем неопределенность типа 0/0, снова продифференцируем полученное выражение:

Y1=lim_P®0[]:

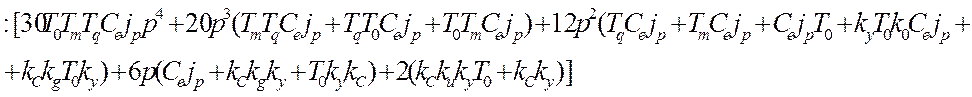
Y1=lim_P®0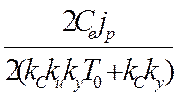= lim_P®0=

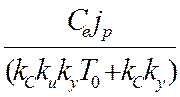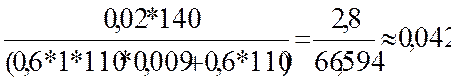
Задача №2

Дана нелинейная система. Определить методом гармонической линеаризации амплитуду и частоту автоколебаний с помощью частотных характеристик.

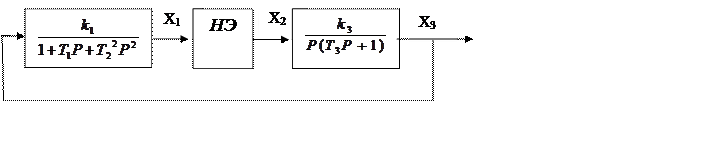
Рис.2.                                                                                           Рис.3.

Таблица №7

Т22	Т1	К1	Т3	К3
0,008	0,06	8	0,09	5

W_н(А)=g(A)+jb(A), передаточная функция нелинейного элемента определяется по формуле: W_н(А)=х₂/х₁,

Предположим, что вся система находится на границе устойчивости и при этом в ней возникли колебания с амплитудой А и частотой w. Составим систему уравнений, описывающих эту систему:

х₁=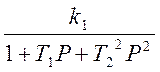* (-х₃)  (1)                х₁=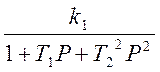*-*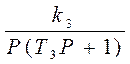х₂      

х₂= W_н(А)*х₁                  (2)                х₁= х₂/W_н(А)

х₃=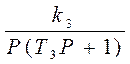х₂             (3)  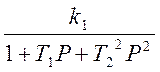  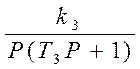            **х₂= -х₂/W_н(А);

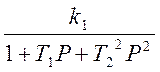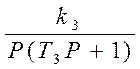*=-1/W_н(А);                  W_л(Р)=-1/W_н(А) (*) – условие возникновения автоколебаний.           W_н(А)= ;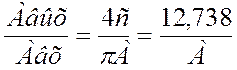 

Для определения частоты и амплитуды автоколебаний необходимо построить 2 характеристики (АФХ линейной части и обратную амплитудную характеристику нелинейной части), т.к. точка пересечения этих характеристик даст нам частоту и амплитуду. Т.е. строим W_Л(jw) и -1/W_Н(А):

W_Л(jw)=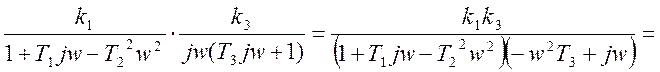

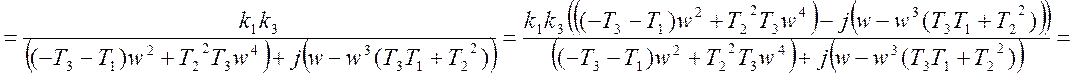
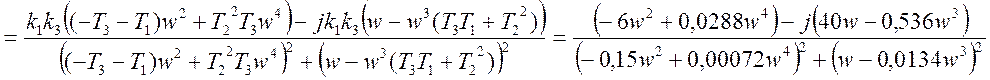Обратная амплитудная характеристика имеет вид: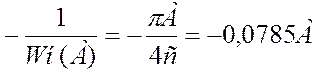

A=;           ;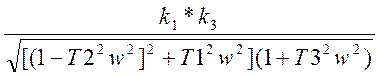

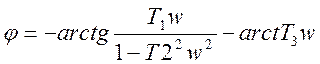A=;           ;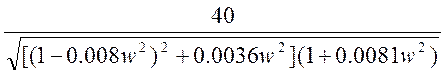

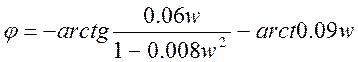Таблица№8

w, c-1	0	1	2	3	4	5	6	7	8	9	10	11	12	¥
A	40	40.1	40.36	40.9	41.6	42.7	44.1	45.8	47.4	48.2	47	43	37	0
, °	0	-8.6	-17.3	-26	-35	-45	-55	-67	-80	-96	-113.5	-132	30.8	0

По табличным данным строим характеристики:

Диаграмма №7

 

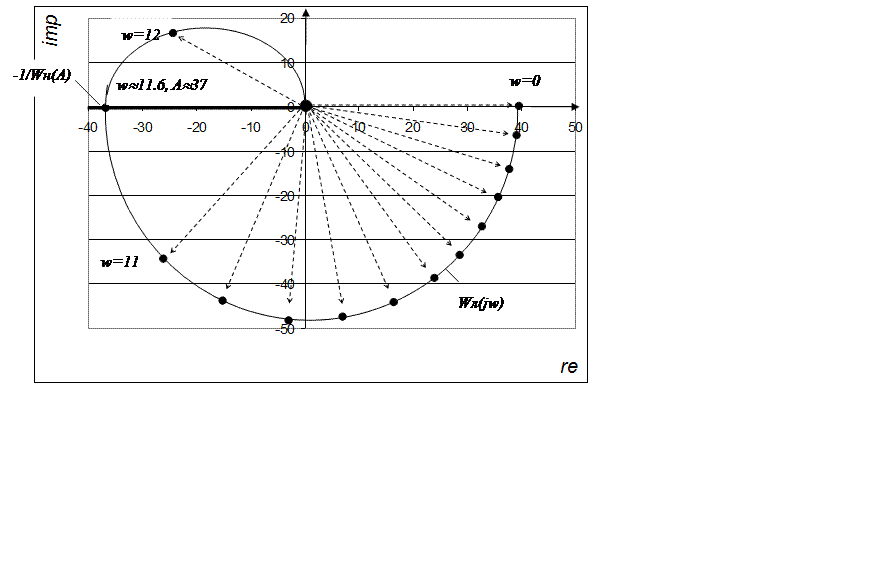Таким образом, методом гармонической линеаризации получаем амплитуду А=37 и частоту w=11,6 с^-1 автоколебаний.