Метод гармонической линеаризации: Методические указания к лабораторной работе, страница 4

          Теперь рассмотрим частотный способ определения параметров автоколебаний. Для этого запишем частотную передаточную функцию разомкнутой системы

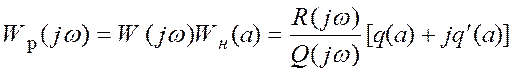                                 .                (32)

Согласно критерию Найквиста в замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы  пройдет через точку (-1, j0). Эти колебания будут устойчивыми, если при возрастании амплитуды на  АФЧХ не будет охватывать точку (-1, j0), при этом колебания затухают и при  АФЧХ будет охватывать точку (-1, j0), при этом колебания расходятся.

          Решим задачу примера1, определив параметры автоколебаний частотным способом. Запишем частотную передаточную функцию разомкнутой системы

                           .

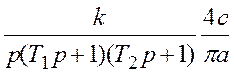АФЧХ  разомкнутой   системы   проходит   через   точку   с   координатами  

(-1, j0) при амплитуде в. Увеличенный фрагмент АФЧХ показан на Рис.15.

                        

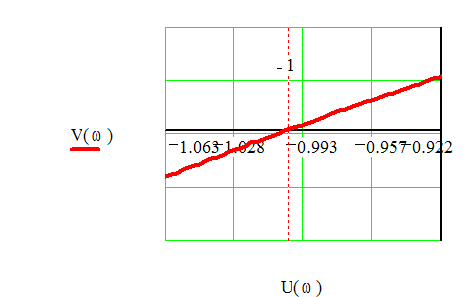
                                                                Рис.15.

Частота колебаний определялась из условий

                                                   ,    .

 Для значений частот              

                                                           ,

были получены следующие значения

                                                                  

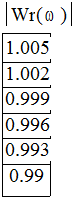
 Откуда . Таким образом, результаты расчетов, выполненные двумя разными способами, практически совпадают. Давая различные по знаку приращения  нетрудно показать, что полученные колебания устойчивые.

          Возможен несколько иной подход к определению периодического решения. Запишем условие возникновения колебаний

                                                       ,                                           (33)

или

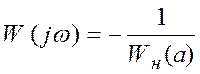                                                        .                                           (34)

Уравнение (34), позволяющее определить параметры колебаний в исследуемой системе решается графически. На комплексной плоскости строятся АФЧХ линейной части  и обратная АФЧХ линеаризованной нелинейности с отрицательным знаком. Точка пересечения этих характеристик и определяет искомые частоту  и амплитуду  колебаний.

          Полученное периодическое решение необходимо исследовать на устойчивость. В замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы  пройдет через точку (-1, j0). Эти колебания будут устойчивыми, если при  АФЧХ не будет охватывать точку (-1, j0) - колебания затухают, а при  АФЧХ будет охватывать точку (-1, j0) - колебания расходятся.

          Таким образом в точке (-1, j0) при  должно выполняться условие

                                                    ,

или

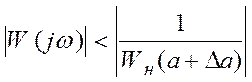                                                 .                                          (35)

Из этого условия следует, что для устойчивости колебаний при увеличении  кривая  должно пересекать кривую  изнутри вовне.

Определим параметры автоколебаний в системе Рис.4, если нелинейный элемент представляет собой чувствительный элемент, имеющий релейную характеристику с зоной нечувствительности и гистерезисом. Линейная часть осталась такой же, как и в примере 1.

Запишем коэффициенты гармонической линеаризации

                                             ,

                                             .

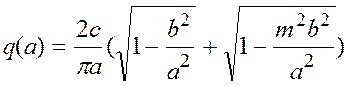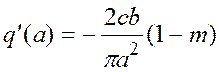В рассматриваемом случае уравнение (34) примет вид

                   .  

Расчеты проводились при   1/сек,  сек, сек,  в,  в и . На Рис.15 и Рис. 16 показаны фрагменты АФЧХ линейной части и отрицательной обратной АФЧХ нелинейной части в разном масштабе. Необходимо отметить, что характеристика нелинейной части образует петлю и дважды пересекается с характеристикой линейной части исследуемой системы. Таким образом, на возможность возникновения колебаний нужно исследовать две точки пересечения.

   

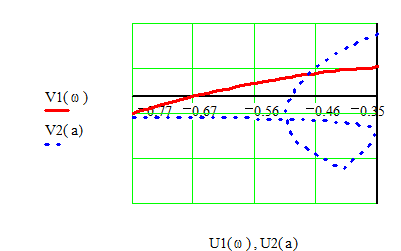
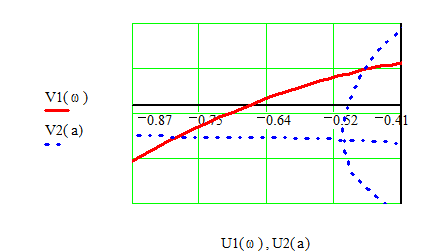
                                   Рис.16.                                                      Рис.17.

Левая точка пересечения имеет координаты U1=-0,784 и V1=-0,0623. Найдем амплитуду колебаний, при которой кривая  наиболее близко проходит через точку с указанными координатами. Амплитуда принимает ряд значений  , при этом координаты точек кривой  равны

                                                                  

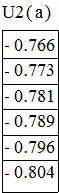
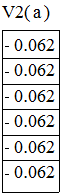
Таким образом .

Аналогично может быть определена амплитуда колебаний в правой  точке пересечения  U2=-0,473 и V2=0,072.  Амплитуда  принимает  значения , при которых

                                                                   

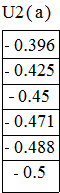
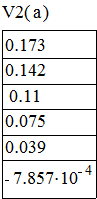
Следовательно .

          Частота  колебаний   для   находится   из   условия   прохождения   кривой  через точку U1=-0,784 и V1=-0,0623. Частота принимает ряд значений 

                                                                     

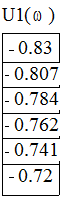
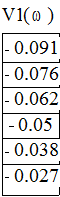
Наиболее близко кривая  проходит через указанную точку при . Частота колебаний  в правой точке .

Проверка устойчивости полученных решений с помощью условия (35) показывает, что колебания в левой точке с амплитудой   и частотой  устойчивы, а в правой точке не устойчивы.

Рассмотренную задачу проще решить с помощью построения АФЧХ разомкнутой системы (32) и применения критерия Найквиста. Увеличенный фрагмент АФЧХ при  приведен на Рис.18.

                              

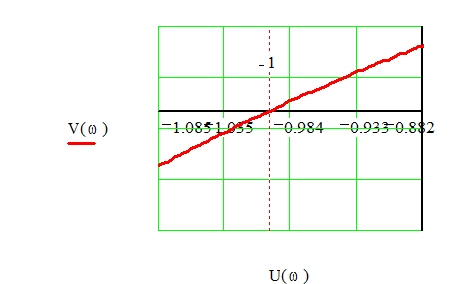
                                                                 Рис.18.

Частота колебаний находится из условия выполнения равенства . Частота принимает значения . Для этих значений модуль равен

                                                                 

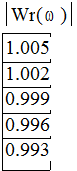
Следовательно, искомая частота колебаний . Нетрудно убедиться, что возникшие колебания устойчивы.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ