Метод гармонической линеаризации: Методические указания к лабораторной работе

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Метод гармонической линеаризации

Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100

Одобрено

редакционно –издательским советом

Балаковского интститута техники,

технологии и управления

Балаково 2004

   Цель работы:  Изучение нелинейных систем с помощью метода гармонической линеаризации (гармонического баланса), определение коэффициентов гармонической линеаризации для различных нелинейных звеньев. Получение навыков по нахождению параметров симметричных колебаний постоянной амплитуды и частоты (автоколебаний), используя алгебраический, частотный способы, а также с помощью критерия Михайлова.

ОСНОВНЫЕ СВЕДЕНИЯ

Метод гармонической линеаризации относится к приближенным методам исследования нелинейных систем. Он позволяет достаточно просто и с приемлемой точностью оценивать устойчивость нелинейных систем, определять частоту и амплитуду установившихся в системе колебаний.

Предполагается, что исследуемая нелинейная САУ может быть представлена в следующем виде

                                             

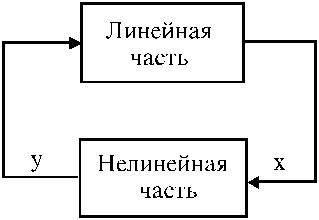
                                                                  Рис.1.

причем нелинейная часть должна иметь одну нелинейность

                                                              .                                                 (1)

Эта нелинейность может быть как непрерывной, так и релейной, однозначной или гистерезисной.

Любую функцию или сигнал можно разложить в ряд по системе линейно-независимых, в частном случае ортонормированных функций. В качестве такого ортогонального ряда может быть использован ряд Фурье.

          Разложим в ряд Фурье выходной сигнал нелинейной части системы

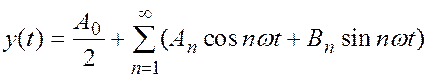                                  ,                               (2)

здесь  - коэффициенты Фурье,

                                                    ,

                                                    ,

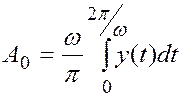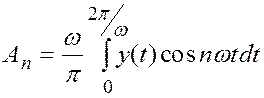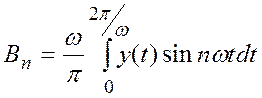                                                    .                                     (3)

Таким образом, сигнал согласно (2) может быть представлен в виде бесконечной суммы гармоник с возрастающими частотами  и т. д.  Этот сигнал поступает на вход линейной части нелинейной системы.

Обозначим передаточную функцию линейной части

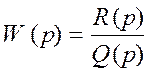                                                             ,                                            (4)

причем степень полинома числителя должна быть меньше степени полинома знаменателя. В этом случае АЧХ  линейной части имеет вид

                                   

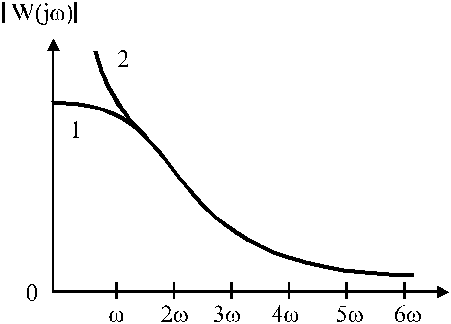
                                                               Рис.2.

где 1 -  не имеет полюсов,  2 -  имеет полюс или полюса.

          Для АЧХ справедливо записать

                                                 .                                  (5)

Таким образом, линейная часть нелинейной системы является фильтром высоких частот. В этом случае линейная часть будет пропускать без ослабления только низкие частоты, высокие же по мере роста частоты будут существенно ослабляться.

В методе гармонической линеаризации делается предположение о том, что линейная часть системы будет пропускать только постоянную составляющую сигнала и первую гармонику. Тогда сигнал на выходе линейной части будет иметь вид

                                          .                                   (6)

Этот сигнал проходит по всему замкнутому контуру системы Рис.1 и на выходе нелинейного элемента без учета более высоких гармоник, согласно (2)  имеем

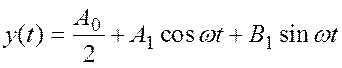                                          .                                   (7)

При исследовании нелинейных систем с помощью метода гармонической линеаризации возможны случаи  симметричных и несимметричных колебаний. Рассмотрим случай симметричных колебаний. Здесь  и.

Введем следующие обозначения

                                                           ,

                                                           .                                                   

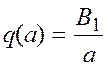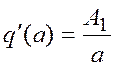Подставив их в (7), получим  .                    (8)

С учетом того, что

                                                ,

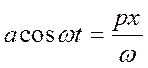                                                ,   где  ,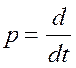 

получим

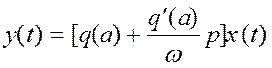                                                 .                                 (9)

Согласно (3) и (8) при

                                            ,

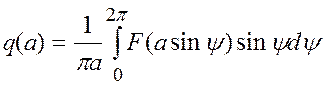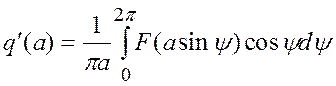                                            .                              (10)

Выражение (9) является гармонической линеаризацией нелинейности  устанавливает линейную связь входной переменной  и выходной  при . Величины и  называются коэффициентами гармонической линеаризации.

          Необходимо отметить, что уравнение (9) является линейным для конкретных величин  и  (амплитуды и частоты гармонических колебаний в системе). Но в целом оно сохраняет нелинейные свойства, так как коэффициенты различны для различных  и . Эта особенность и позволяет исследовать с помощью метода гармонической линеаризации свойства нелинейных систем  [ Попов Е.П.].

          В случае несимметричных колебаний гармоническая линеаризация нелинейности приводит к линейному уравнению

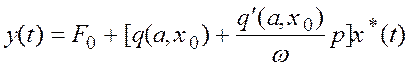                                  ,                         (11)

где

                                         ,

                                         ,

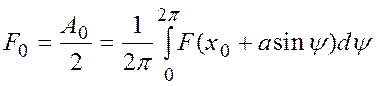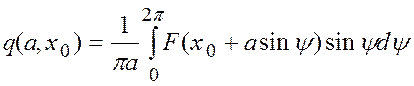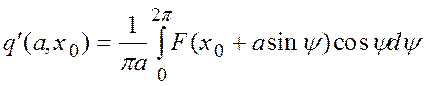                                         .                 (12)

Так же как и уравнение (9), линеаризованное уравнение (11) сохраняет свойства нелинейного элемента, так как коэффициенты гармонической линеаризации , , а так же постоянная составляющая  зависят и от смещения  и от амплитуды гармонических колебаний .

Уравнения (9) и (11) позволяют получить передаточные функции гармонически линеаризованных нелинейных элементов. Так для симметричных колебаний

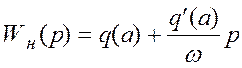                                                 ,                                    (13)

при этом частотная передаточная функция

                                                                                     (14)

зависит только от амплитуды и не зависит от частоты колебаний в системе.

Необходимо отметить, что если нечетно-симметричная нелинейность однозначна, то в случае симметричных колебаний в соответствии с (9) и (10) получим, что                               ,                                                 (15)

так как

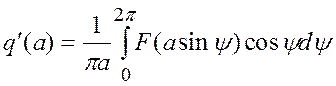
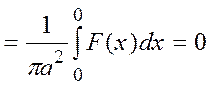                                           (16)            

и линеаризованная нелинейность имеет вид

                                                            .                                        (17)

Для неоднозначных нелинейностей (с гистерезисом) интеграл в выражении (16) не равен нулю, вследствие различия в поведении кривой при возрастании и убывании , поэтому справедливо полное выражение (9).

          Найдем коэффициенты гармонической линеаризации для некоторых нелинейных характеристик. Пусть нелинейная характеристика имеет вид релейной характеристики с гистерезисом и зоной нечувствительности. Рассмотрим, как гармонические колебания проходят через нелинейный элемент с такой характеристикой.



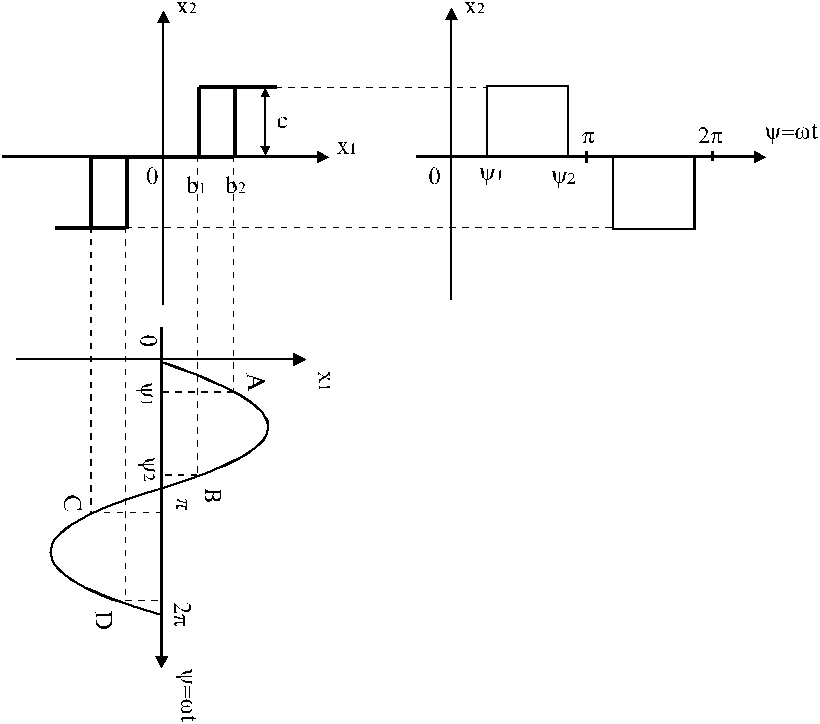
                                                                Рис.3.

При выполнении условия   , то есть если амплитуда входного сигнала  меньше зоны нечувствительности , то сигнал на выходе нелинейного элемента отсутствует.  Если же амплитуда , то реле переключается в точках A, B, C и D. Обозначим  и .

          Тогда