Метод гармонической линеаризации: Методические указания к лабораторной работе, страница 3

                                Рис.5.                                                        Рис.6.

Частоту колебаний при этом можно найти из условия равенства нулю модуля . Для частот 

                                                  

значения модуля сведены в таблицу

                                                          

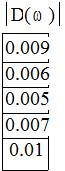
Таким образом, частота колебаний 6,38 . Необходимо отметить, что точность расчетов легко может быть увеличена.

Полученное периодическое решение, определяемое значением амплитуды  и частоты , необходимо исследовать на устойчивость. Если решение устойчиво, то в системе имеет место автоколебательный процесс (устойчивый предельный цикл). В противном случае предельный цикл будет неустойчивым.

Проще всего для исследования устойчивости периодического решения использовать критерий устойчивости Михайлова в графическом виде. Было установлено, что при  кривая Михайлова проходит через начало координат. Если дать  малое приращение , то кривая займет положение либо выше нуля, либо ниже. Так в последнем примере дадим приращение  в, то есть  и .  Положение кривых Михайлова показано на Рис.7.

                         

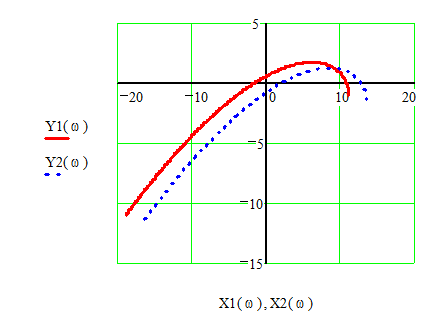
                                                                  Рис.7.

При  кривая проходит выше нуля, что говорит об устойчивости системы и затухающем переходном процессе. При  кривая Михайлова проходит ниже нуля, система является неустойчивой и переходный процесс является расходящимся. Таким образом периодическое решение с амплитудой в и частотой колебаний 6,38  устойчиво.

Для исследования устойчивости периодического решения может быть использован и аналитический критерий, получаемый из графического критерия Михайлова. Действительно, чтобы узнать пойдет ли кривая Михайлова при  выше нуля достаточно посмотреть, куда будет перемещаться точка кривой Михайлова, которая при  находится в начале координат.

                                               

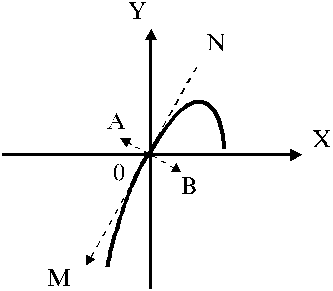
                                                                  Рис.8.

Если разложить перемещение этой точки по координатным осям X и Y, то для устойчивости периодического решения вектор, определяемый проекциями на координатные ос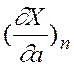и

                                                           и ,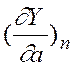

должен быть расположен справа от касательной MN к кривой Михайлова, если смотреть вдоль кривой в сторону возрастания , направление которой определяется проекциям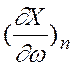и

                                                          и .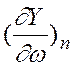

Аналитическое условие устойчивости запишем в следующем виде

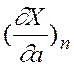
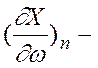
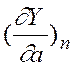
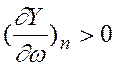                                            .                            (31)

В этом выражении частные производные берутся по текущему параметру  кривой Михайлова

                      ,

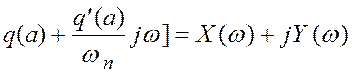в точке .

Необходимо отметить, что аналитическое выражение критерия устойчивости (31) справедливо только для систем не выше четвертого порядка, так как например для системы пятого порядка в начале координат условие (31) может выполняться, а система будет неустойчивой

                                               

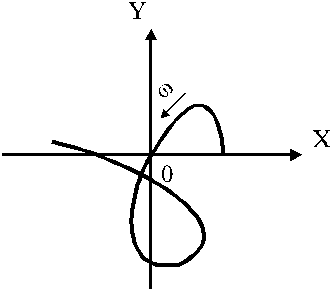
                                                                  Рис.9.

Применим критерий (31) для исследования устойчивости периодического решения, полученного в примере 1.

Так как

                                            ,

                                             ,

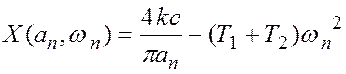то

                                 ,        ,

                                 ,     .

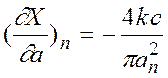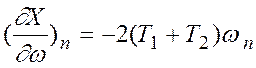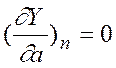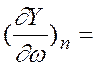
Следовательно

                                     .

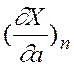
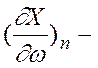
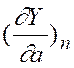
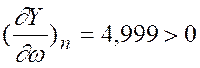Таким образом, периодическое решение, полученное в примере 1 устойчиво.

Интересно провести сравнение исследования систем с помощью приближенного метода гармонической линеаризации и точных методов исследования - фазовой плоскости и припасовывания. Приведем результаты моделирования в MATHCAD 7 нелинейной системы, рассмотренной в примере 1.

Как видно из Рис.10 фазовые траектории образуют устойчивый предельный цикл

                  

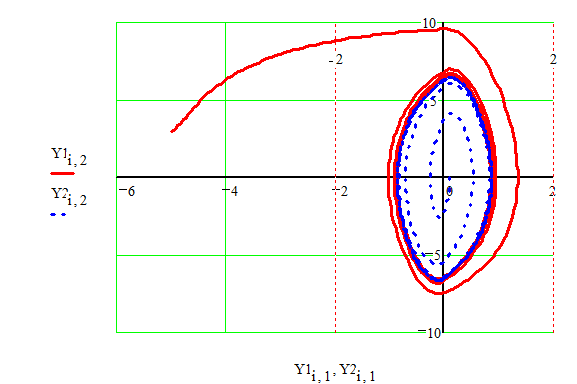
                                                                     Рис.10.

Амплитуду и частоту автоколебаний можно найти из переходного процесса

                  

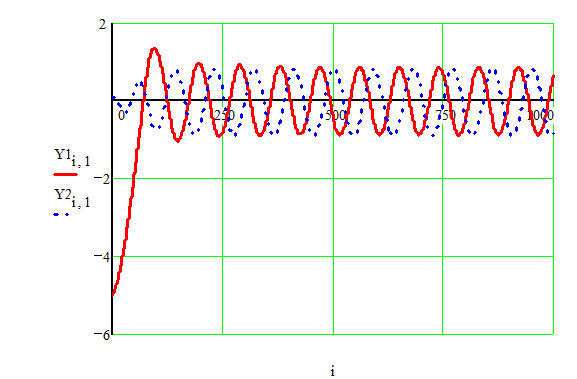
                                                                  Рис.11.

Амплитуда колебаний  в и частота  , что говорит о практическом совпадении результатов, так как в и .

Рассмотрим пример 3 исследования нелинейной САУ с помощью метода гармонической линеаризации. Будем исследовать нелинейную систему  Рис.4, если нелинейный элемент представляет собой чувствительный элемент, имеющий  релейную характеристику с зоной нечувствительности. Линейная часть осталась без изменения.

Коэффициенты гармонической линеаризации при этом равны

                                                      ,

                                                      .

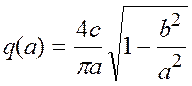Для нахождения периодического решения построим кривую Михайлова

                     ,

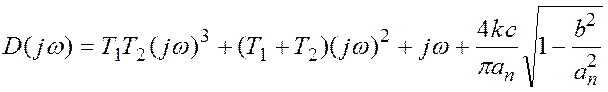при  1/сек,  сек, сек,  в и в.

                             

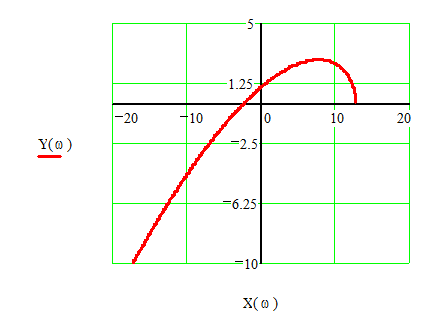
                                                          Рис.12.

Кривая Михайлова построена при значении амплитуды в, при которой она наиболее близко подходит к началу координат. Вместе с тем, не удается подобрать значение , при котором кривая Михайлова проходила бы через начало координат. Этот факт говорит о том, что при таких параметрах в системе не возможны автоколебания.

Рассматриваемая система имеет следующий вид фазовых траекторий и переходных процессов

                          

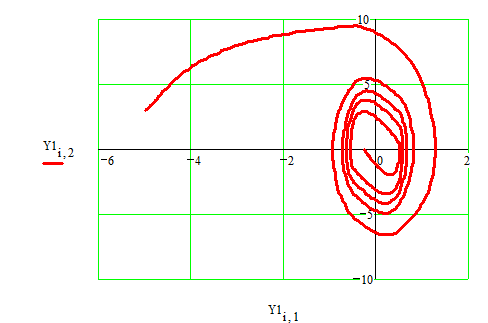
                                                                     Рис.13.

                           

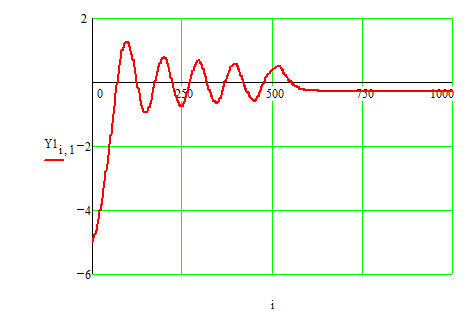
                                                             Рис.14.

Как видим в исследуемой системе отсутствуют автоколебания.