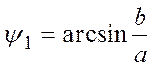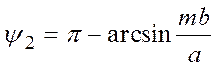Метод гармонической линеаризации: Методические указания к лабораторной работе, страница 2

                                                         ,                            

                                                         .                                   (18)

          При вычислении коэффициентов гармонической линеаризации  следует иметь ввиду, что при симметричных нелинейных характеристиках интегралы в выражениях (10) находятся на полупериоде (0, p) с последующим увеличением результата в два раза. Таким образом

       ,

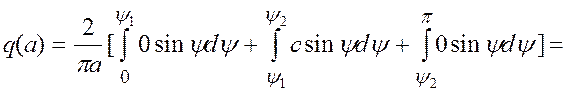
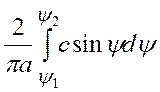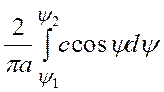        .                                                                                (19)

Тогда

                        ,

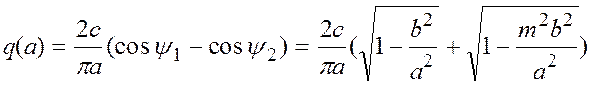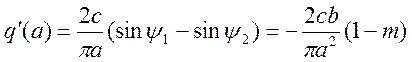                         .                              (20)

          Для нелинейного элемента с релейной характеристикой и зоной нечувствительности

                                                           ,

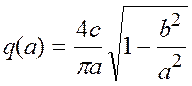                                                           .                                                   (21)

          Для нелинейного элемента, имеющего релейную характеристику с гистерезисом

                                                       ,

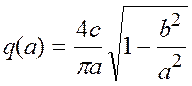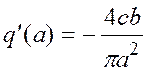                                                        .                                               (21)

Аналогично могут быть получены коэффициенты гармонической линеаризации для других нелинейных характеристик.

          Рассмотрим два способа определения симметричных колебаний постоянной амплитуды и частоты (автоколебаний) и устойчивости линеаризованных систем: алгебраический и частотный. Сначала рассмотрим алгебраический способ.  Для замкнутой системы Рис.1 передаточная функция линейной части равна

                                                          .

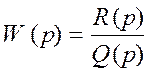Запишем гармонически линеаризованную передаточную функцию нелинейной части

                                                 .

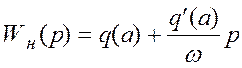Характеристической уравнение замкнутой системы имеет вид

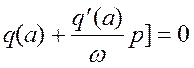                                             .                          (22)

Если в исследуемой системе возникают автоколебания, то это говорит о наличии двух чисто мнимых корней в ее характеристическом уравнении. Поэтому подставим в характеристическое уравнение (22) значение корня .

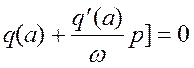                                    .                     (23)

Представим

                                              .

Получим два уравнения, определяющих искомую амплитуду  и частоту

                                                          ,

                                                          .                                            (24)

Если в решении возможны вещественные положительные значения амплитуды  и частоты , то в системе могут возникнуть автоколебания. Если же амплитуда  и частота  не имеет положительных значений, то автоколебания в системе невозможны.

          Рассмотрим пример 1. Пусть исследуемая нелинейная система имеет вид

                                                                 Рис.4.

          В этом примере нелинейный элемент представляет собой чувствительный элемент с  релейной характеристикой, для которого коэффициенты гармонической линеаризации

                                                              ,

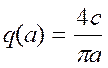                                                              .                                                (25)

Исполнительное устройство имеет передаточную функцию вида

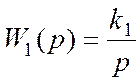                                                      .                                               (26)  

Передаточная функция объекта регулирования равна

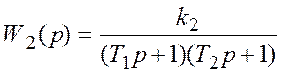                                                .                                  (27)

Передаточная функция линейной части системы

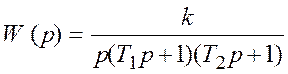                                                ,                                 (28)

где  .

          На основании (22), (25) и (28) запишем характеристическое уравнение замкнутой системы

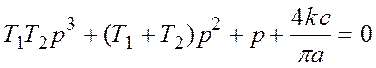                                           ,                             (29)

откуда

                                         ,

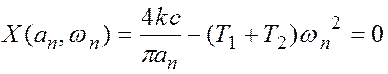                                         .                                        (30)

Пусть  1/сек,  сек, сек,  в.

В этом случае параметры периодического движения равны

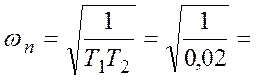                                     7,071 ,

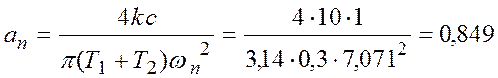                                      в.

          Рассмотрим способ определения параметров автоколебаний в линеаризованной САУ с помощью критерия Михайлова. Способ основан на том, что при возникновении автоколебаний система будет находиться на границе устойчивости и годограф Михайлова в этом случае будет проходить через начало координат.

          В примере 2 найдем параметры автоколебаний при том условии, что нелинейный элемент в системе Рис.4 представляет собой чувствительный элемент, имеющий релейную характеристику с гистерезисом, для которого коэффициенты гармонической линеаризации

                                                        ,

                                                        .

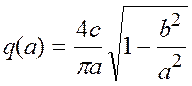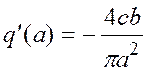Линейная часть осталась неизменной.

Запишем характеристическое уравнение замкнутой системы

                      .

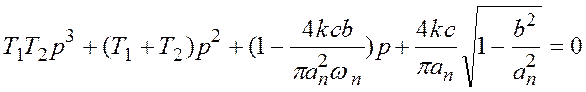Годограф Михайлова получается заменой .

                     .

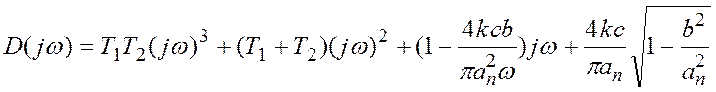          Задача заключается в том, чтобы подобрать такую амплитуду колебаний , при которой годограф пройдет через начало координат. Необходимо отметить, что при этом текущая частота , так как именно в этом случае кривая пройдет через начало координат.

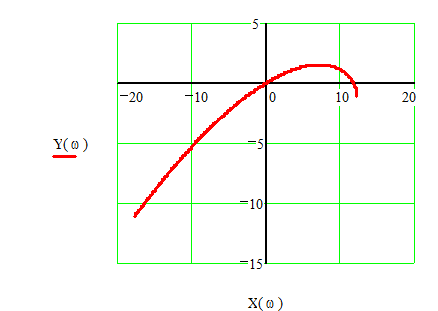
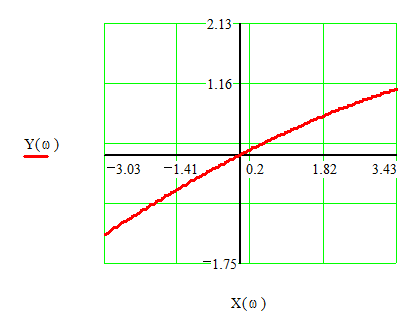
          Расчеты, проведенные в MATHCAD 7 при  1/сек,  сек, сек,  в и в, дали следующие результаты. На Рис.5 годограф Михайлова проходит через начало координат. Для повышения точности расчетов увеличим нужный фрагмент графика. На Рис.6 приведен фрагмент годографа, увеличенный в окрестности начала координат. Кривая проходит через начало координат при в.