Міністерство освіти і науки України
Національний технічний університет України
«Київський політехнічний інститут»
Контрольна робота
по курсу «Теорія автоматичного управліня»
тема:
«Линейная САУ «Разомкнутый принцип управления»
Варіант № 5
Виконав:
Студент IІI курсу ФІОТ
Групи
.
Перевірив:
Київ – 2011
 |
![]()
![]()
|
|


|
|
|
|
|
|
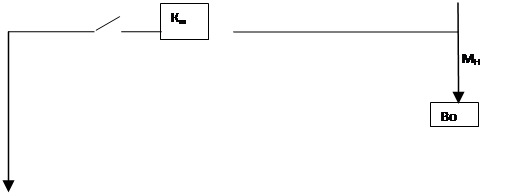
Структурная схема
Задание:
1. Построить математическую модель САУ.
2. Составить дифференциальное уравнение САУ по задающему и возмущающему воздействиям.
3. Определить передаточные функции САУ по входному сигналу G(t) и возмущению Мн(t).
3.1.Определить передаточную функцию по входу от задающего воздействия при равенстве нулю возмущающего воздействия при нулевых начальных условиях.
3.2.Определить передаточную функцию по входу от возмущающего воздействия при равном нулю задающего воздействия при нулевых начальных условиях.
3.3. Определить передаточную функцию по входу от возмущающего воздействия при неравенстве 0 G(t) и при нулевых начальных условиях когда канал компенсации замкнут.
3.4.Определить закон управления.
4.Определить временные характеристики.
4.1.Рассмотреть САУ при МH(t)=0, а входное воздействие G(t)=1(t) – скачок, y(0)=0, а перваяпроизводная y'(0)=0.
4.2.Рассчитать и построить переходную функцию.
4.3. Рассчитать функцию веса.
5.Частотные характеристики (рассчитать и построить).
5.1.Амплитудно-фазочастотная характеристика (АФЧХ), когда МН(t)=0.
5.2.Амплитудно-частотную характеристику
5.3.Фазочастотную характеристику
5.4.Логорифмитическая амплитудно-частотная характеристика.
|
Кпе |
Кпр |
Ку |
Ко |
Кр |
Ту |
То |
Bo |
|
1,25 |
2 |
4 |
1 |
0,75 |
0,1 |
0,3 |
1 |
Перерисуем схему с передаточными функциями звеньев:
![]()
![]()
![]()
![]()
![]()
![]()
|


|
|
|
|
![]()
|
|
|
где
W1= Km ; W2= B0
; W3= Кпе ; W4=
Кпр ; W5=
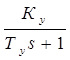 ; W6=
K0 ; W7=
; W6=
K0 ; W7= 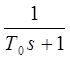 ; W8=
Kp
; W8=
Kp
общий коэффициент усиления:
K = Кпе* Кпр*Ky* K0* Kp = 1.25*2*4*1*0.75=7,5
Преобразуем схему:
![]()
![]()
![]()
![]()
![]()
|


|
|
|
|
|
|
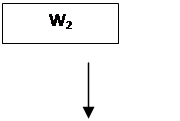 |
|||
AD
![]()
![]()
|
|


1.Построить математическую модель САУ.
Запишем математическую модель системы, когда на нее действует задающий, возмущающий сигналы и когда канал компенсации замкнут:
Y(s)
= С-D
= (В*W3*W4*W5*W6
- Мн(s)*W2)*W7*W8
= [(G(s)+A) * W3*W4*W5*W6 - Мн(s)* *W2]*W7*W8
= [(G(s)+МН(s)*
![]() ) * W3*W4*W5*W6
- Мн(s)* W2]*W7*W8
= = [G(s)* W3*W4*W5*W6
+ МН(s)*W1*
W4*W5*W6 - Мн(s)*W2]*W7*W8
=
) * W3*W4*W5*W6
- Мн(s)* W2]*W7*W8
= = [G(s)* W3*W4*W5*W6
+ МН(s)*W1*
W4*W5*W6 - Мн(s)*W2]*W7*W8
=
=
[G(s) * ![]() + МН(s)*
(
+ МН(s)*
(![]() - B0)]
*
- B0)]
*![]()
Найдем при каком значении Кm будет полностью компенсироваться возмущающее воздействие:
![]() - B0 = 0 => Кm =
- B0 = 0 => Кm = ![]() =
= ![]() = 0.125
= 0.125
Т.к. ключ разомкнут, то канал компенсации равен 0, т.е. МН(s)*W1* W4*W5*W6 =0, поэтому далее рассматривается математическая модель при разомкнутом ключе:
Y(s)= G(s)* W3*W4*W5*W6*W7*W8 - Мн(s)*W2*W7*W8
2. Составить дифференциальное уравнение САУ по задающему и возмущающему воздействиям.
Дифференциальное ур-е САУ по задающему воздействию :
где, МН(t)=0 => Мн(s)* W2*W7*W8 = 0 ,
следовательно Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
=
G(s) * ![]() ,
,
тогда
(Ту*s+1)*(To*s+1)*Y(s)=G(s)*Кпе*Кпр*Ку*Ко*Кр
(Ту*То*s2 + (Ty+To)*s + 1)*Y(s) =G(s)*Кпе*Кпр*Ку*Ко*Кр
Ту*То*Y(s)*s2 + (Ty+To)*Y(s)*s + Y(s) = G(s)*Кпе*Кпр*Ку*Ко*Кр
Учитывая,
что S = ![]() , имеем обратное преобразование
, имеем обратное преобразование
Ту*То*у``(t) + (Ty+To)*y`(t) + y(t) = g(t)*Кпе*Кпр*Ку*Ко*Кр
Подставив значения, получим:
0,03*y``(t) + 0,4*y`(t) + y(t) = 7,5*g(t)
Дифференциальное ур-е САУ по возмущающему воздействию:
где, g(t)=0 => G(s)* W3*W4*W5*W6*W7*W8 = 0
следовательно
Y(s) =- Мн(s)*W2*W7*W8 = -MH(s) * ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.