Електронна оптика електростатичних полів». Розподіл потенціалу в аксиально-симетричному електричному полі, страница 8

' Записуємо дані в лист Exlel

With Worksheets("Лист1")

For n = 1 To 20

For m = 1 To 84

.Cells(n + 1, m + 1).Value = a(m, n)

Next m

Next n

End With

End Sub

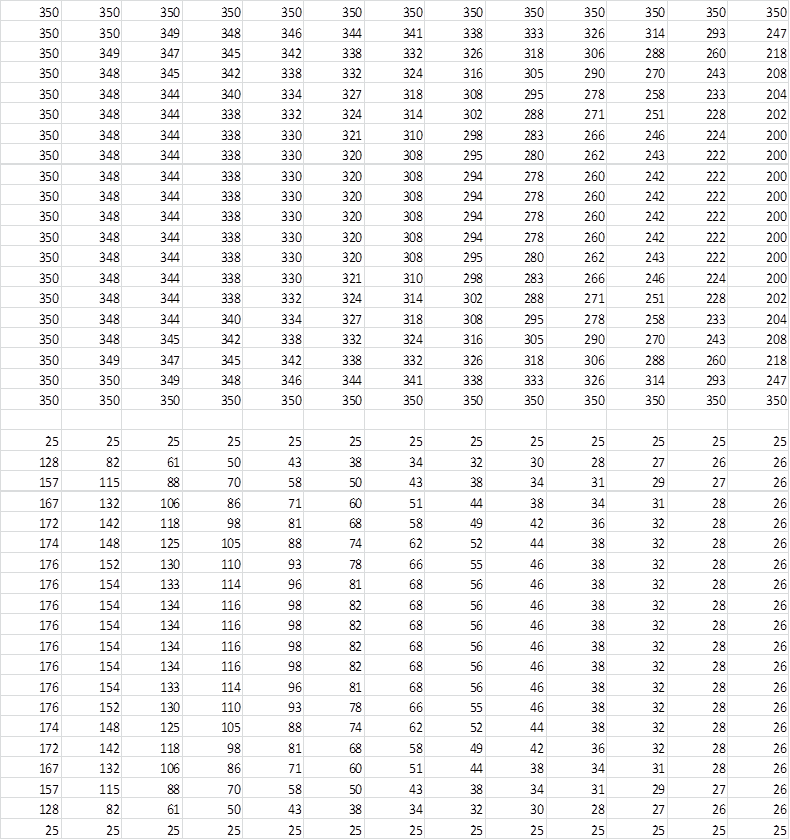
Дані, отримані під час розрахунку на 10 ітерації подано в таблиці 2.2.1:

Всі потенціали лівіше дорівнюють 350, правіше - 25

Починаючи з 29-го кроку по 65-й

Табл.. 2.2.1

На основі отриманих даних будуємо графіки

2.5 Графіки

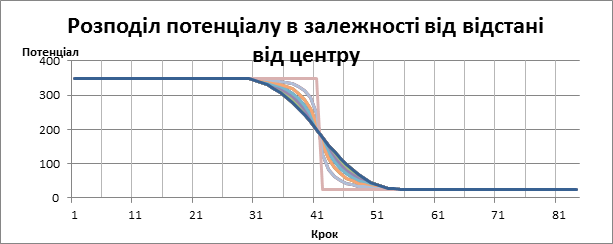
рис 2.7.1 Розподіл потенціалу в залежності від відстані від центру та координати

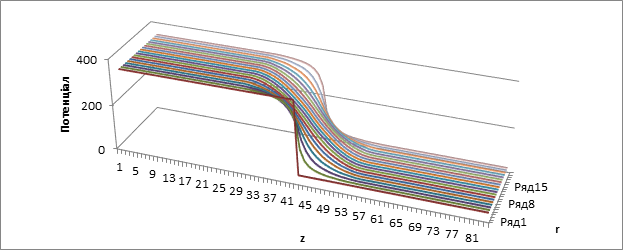
рис 2.7.2 Розподіл потенціалу в залежності від відстані від центру та координати z

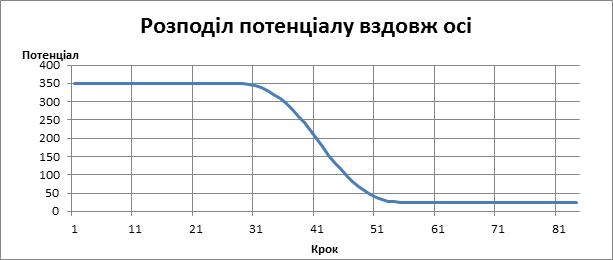
рис 2.7.3 Розподіл потенціалу вздовж осі

Перевірка за допомогою програми LINZA

Задамо геометричні параметри та потенціали електродів імерсійної лінзи відповідно до свого варіанту (варіант 14)

Тип лінзи	Потенціал, В	Координати x,y	Радіус/розмір, мм
Діафрагма	350	0,0	5
Циліндр	350	0,5	20
Циліндр	25	21,5	20
Діафрагма	25	41,0	5

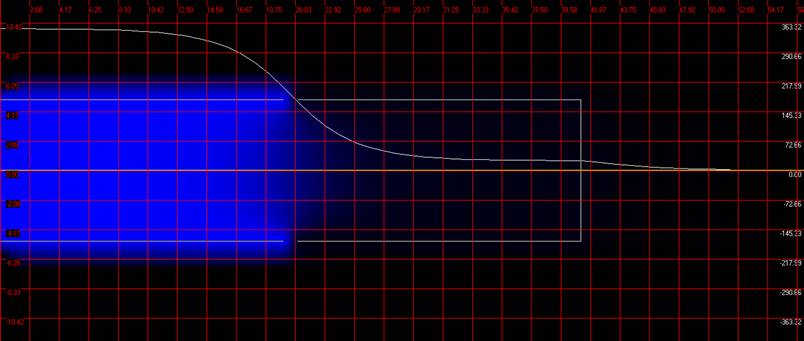
Рис. 2.9. Картина поля імерсійної лінзи і розподіл потенціалу в полі імерсійної лінзи

Дані отримані за допомогою методу кінцевих різниць для розрахунку електростатичного поля, і дані, отримані за допомогою програми LINZA співпадають.

2.2.2  Лінза-діафрагма.

1)  Задамо геометричні параметри та потенціали електродів лінзи відповідно до рис.2.1.

Тип лінзи	Потенціал, В	Координати x,y	Радіус/розмір, мм
Діафрагма	25	0,0	5
Діафрагма	25	5,1	4
Діафрагма	350	10,1	5

       у

U₁=25В            U₂=25В           U₃=350В                                            

                                                           

5                        4                     5

u_х

 

                                                                                                                         x

(0,0)                  (5,1)                (10,1)                                                    

Рис. 2.1. Геометричні розміри системи лінзи-діафрагми.

Картина поля для лінзи-діафрагми із заданими параметрами показана на рис.2.2.

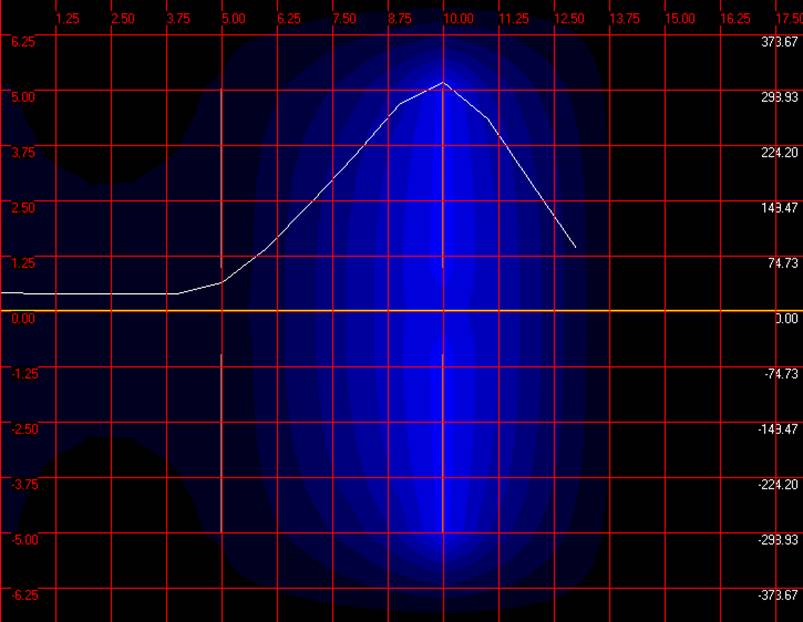
Рис. 2.2. Картина поля лінзи-діафрагми і розподіл потенціалу в полі лінзи-діафрагми.

2) Дослідимо траєкторію руху електрона у полі лінзи, для цього задамо параметри влету електрона: 

Частинка	точка влету	кут влету
Електрон	-2	0

Траєкторію руху єлектрона показано на рис.2.3.

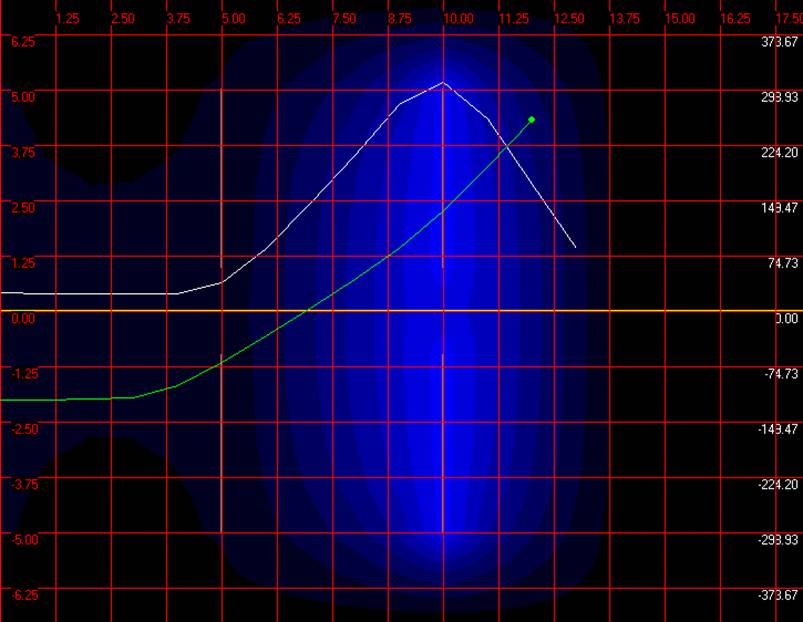
Рис.2.3. Траекторія руху електрона в полі лінзи-діафрагми.

Фокусна відстань у цьому випадку дорівнює 6.87 мм.

Як видно з рис. 2.3, електрон відхиляється до осі симетрії лінзи, тобто лінза є збираючою, пояснюється це наступним. Напрям сили, що діє на електрон в області лінзи, визначається знаком другої похідної U₀"(z). Це випливає з аналізу основного рівняння електронної оптики (1.11). Радіальна сила, що діє на електрон визначається рівнянням (1.12), з якого слідує, що якщо U₀"(z) > 0, то це відповідає наростанню напруженості поля вздовж осі z. Радіальна сила направлена протилежно до r, тобто направлена до осі z. Електрон рухається прямолінійно у однорідному полі,потрапляючи у неоднорідне поле електрон під дією радіальної сили починає рухатися до осі.

Запустимо ще три електрони:

Частинка	точка влету	кут влету
Електрон	2	0
Електрон	-1	0
Електрон	1	0