Електронна оптика електростатичних полів». Розподіл потенціалу в аксиально-симетричному електричному полі, страница 4

  

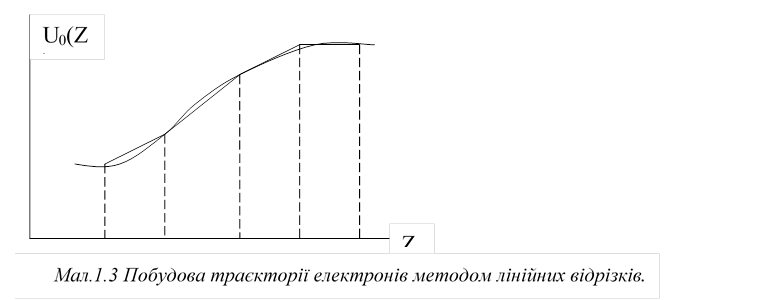
При такому представленні усередині кожної ділянки U₀(z) = kz, U₀^I(z) = const,

U₀^II(z) = 0. На границях ділянок U₀^II(z) переходить у нескінченність.

Обозначимо координати границь ділянок через z₁, z₂, z₃, …, z_n, значення осьового потенціалу на границях ділянок через U₁, U₂, U₃, …, U_n, значення перших похідних dU₀/dz усередині ділянок через U₁^I, U₂^I, U₃^I, …, U_n^I  і віддалення траєкторій від осі на границях ділянок через r₁, r₂, …, r_n .  Оскільки усередині кожної ділянки U₀^II(z) = 0, вираз (1.11) для ділянок, що знаходяться між площинами з координатами (z₁, z₂), (z₂, z₃), …, (z_n-1, z_n-2), приймає вигляд

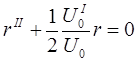,                                                       (1.17)

де диференціювання іде по змінній z. Перепишемо рівняння (1.17) у вигляді

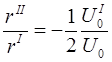                                                          (1.18)

і проінтегруємо по z усередині ділянки від z₁ до деякого значення z, що лежить між z₁ і z_2:

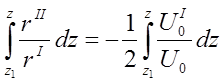.                                              (1.19)

Неважко побачити, що підінтегральні функції зручно представити логарифмами, тобто перетворити (1.19) у рівняння

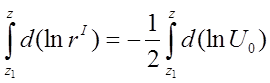 ,                                      (1.20)

яке після інтегрування запишеться як

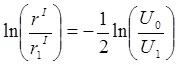,                                                              (1.21)

де r₁ = (dr/dz)_z1 (праворуч від площини з координатою z₁).

З (1.21) безпосередньо виходить, що усередині розглянутої ділянки

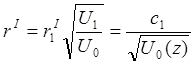                                                   (1.22)

Тут  - стала, що визначається початковими умовами – нахилом дотичної до траєкторії і значенням потенціалу в точці z₁.

Інтегрування рівняння (1.22) в границях ділянки призводить до виразу для r(z) усередині ділянки, що розглядається:

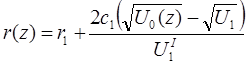                                           (1.23)

де .

На правій границі ділянки (при z = z₂)

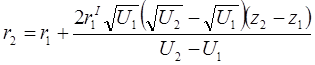                                            (1.24)

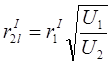
(індекс l вказує на кут нахилу траєкторії зліва від границі розділу першої і другої ділянки).

Вираз (1.24) дозволяє побудувати відрізок траєкторії параксіального електрону усередині ділянки, що обмежовується площинами, перпендикулярними до осі, в границях від z₁ до z₂.

Величина r₂, що підрахована в кінці першої ділянки, використовується як початкова при розрахунку траєкторії у другій ділянці. Але значення , що було підраховане в кінці першої ділянки не можна вважати початковим для розрахунку траєкторії у другій ділянці, так як при переході через границю ділянок  терпить розрив і траєкторія має злам, тобто не дорівнює  (індекс p вказує на кут нахилу траєкторії справа від границі розподілу ділянок).

Для підрахунку кута нахилу траєкторії на початку другої ділянки  скористуємось тим, що в околиці точки z₂ значення U₀(z) і U₀^І (z) залишаються кінцевими, а значення U₀^ІІ обертається у нескінченність. На підставі цього поблизу границь ділянок в рівнянні (1.11) можна не враховувати величину (U₀^І /2U₀)r^І порівняно з (U₀^ІІ /4U₀)r, тобто представити (1.11) у вигляді

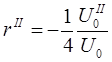                                                     (1.25)

Можна також припустити, що в області U₀(z) = U₀(z₂) =const. Тоді інтегрування рівняння (1.25) в границях між точками z_2l і z_2p, що лежать близько до z₂, приводить до виразу

,                                          (1.26)

де  .

Визначив з (1.24) і (1.26) r₂ і  і прийняв їх за початкові дані для лівої границі другої ділянки, знаходять траєкторії на другій ділянці, визначають r₃ і , приймають їх за початкові дані для третьої ділянки і т.д. Таким чином може бути знайдена уся траєкторія електрону у при осьовій області електричного поля, що має властивості осьової симетрії.

1.4  Лінза-діафрагма

Лінза-діафрагма утворюється диском із круглим отвором, що має деякий потенціал Uд. По обидва боки до диска примикають області постійної, але різної з кожної сторони напруженості електричного поля Е1 і Е2. В деяких випадках одне з полів може бути відсутнім (Е1 = 0 чи Е2 = 0). Очевидно, поблизу отвору діафрагми напруженість поля буде змінюватися уздовж осі  ; саме ця область поля і буде власне лінзою.